Convex Polygons - Definition, Examples, Quiz, FAQ, Trivia
Learn all about convex polygons with simple explanations, visual examples, and interactive quizzes
What is a Convex Polygon?
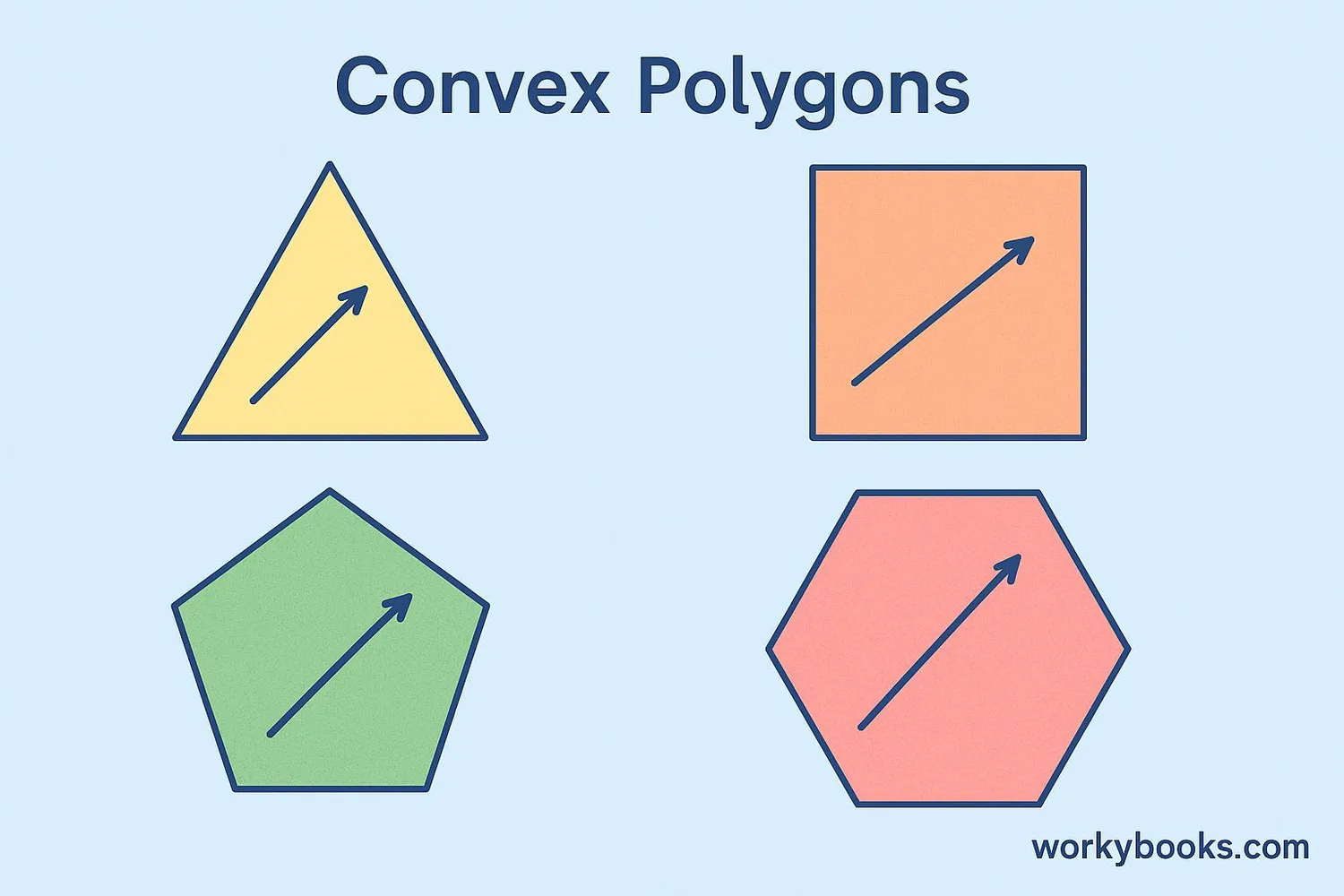
A convex polygon is a closed shape with straight sides where all interior angles are less than 180 degrees, and any line segment connecting two points inside the polygon stays completely within it.
Think of a convex polygon like a stretched rubber band - it has no dents or indentations. All the corners point outward, and if you were to walk around its perimeter, you would only make left turns or only right turns.
Convex polygons are important in geometry because they have special properties that make them easier to work with than other shapes.
Key Concept
A polygon is convex if you can draw a straight line between any two points inside it without leaving the polygon.
Properties of Convex Polygons
Convex polygons have several special properties that make them different from other shapes:
1. All interior angles are less than 180 degrees: Each corner of the polygon doesn't bend inward.
2. No dents or indentations: The outline of the polygon is always curving outward.
3. Line segments stay inside: If you pick any two points inside the polygon, the straight line connecting them will always stay within the shape.
4. Diagonals are inside: All diagonals (lines connecting non-adjacent corners) stay completely inside the polygon.
5. Single interior region: Convex polygons have just one interior region with no holes or separate sections.
Remember
All regular polygons (with equal sides and angles) are convex, but not all convex polygons are regular.
Concave vs Convex Polygons
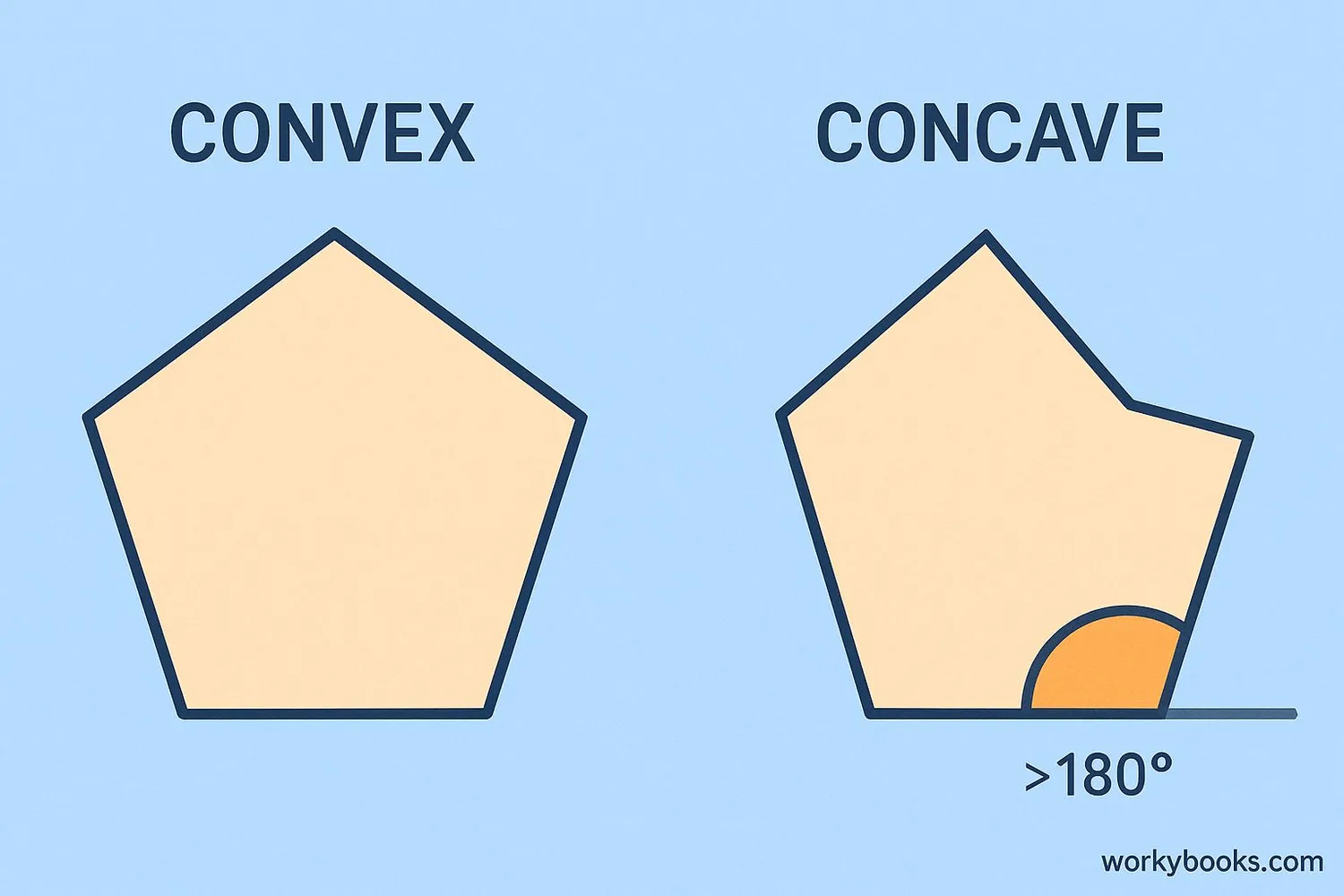
The main difference between convex and concave polygons is their shape:
- All interior angles < 180°
- No dents or indentations
- All diagonals inside
- Line segments stay inside
- At least one interior angle > 180°
- Has at least one "dent"
- Some diagonals outside
- Some line segments exit the shape
An easy way to remember: "Convex" shapes curve outward like the surface of a ball, while "concave" shapes curve inward like a cave.
Types of Convex Polygons
Convex polygons are classified by the number of sides they have:
| Number of Sides | Polygon Name | Example |
|---|---|---|
| 3 | Triangle | Equilateral triangle |
| 4 | Quadrilateral | Square, rectangle |
| 5 | Pentagon | Regular pentagon |
| 6 | Hexagon | Regular hexagon |
| 7 | Heptagon | Regular heptagon |
| 8 | Octagon | Stop sign shape |
| 9 | Nonagon | Regular nonagon |
| 10 | Decagon | Regular decagon |
Each of these polygons can be convex as long as they follow the properties we discussed: no interior angles greater than 180° and no dents.
Sum of Interior Angles
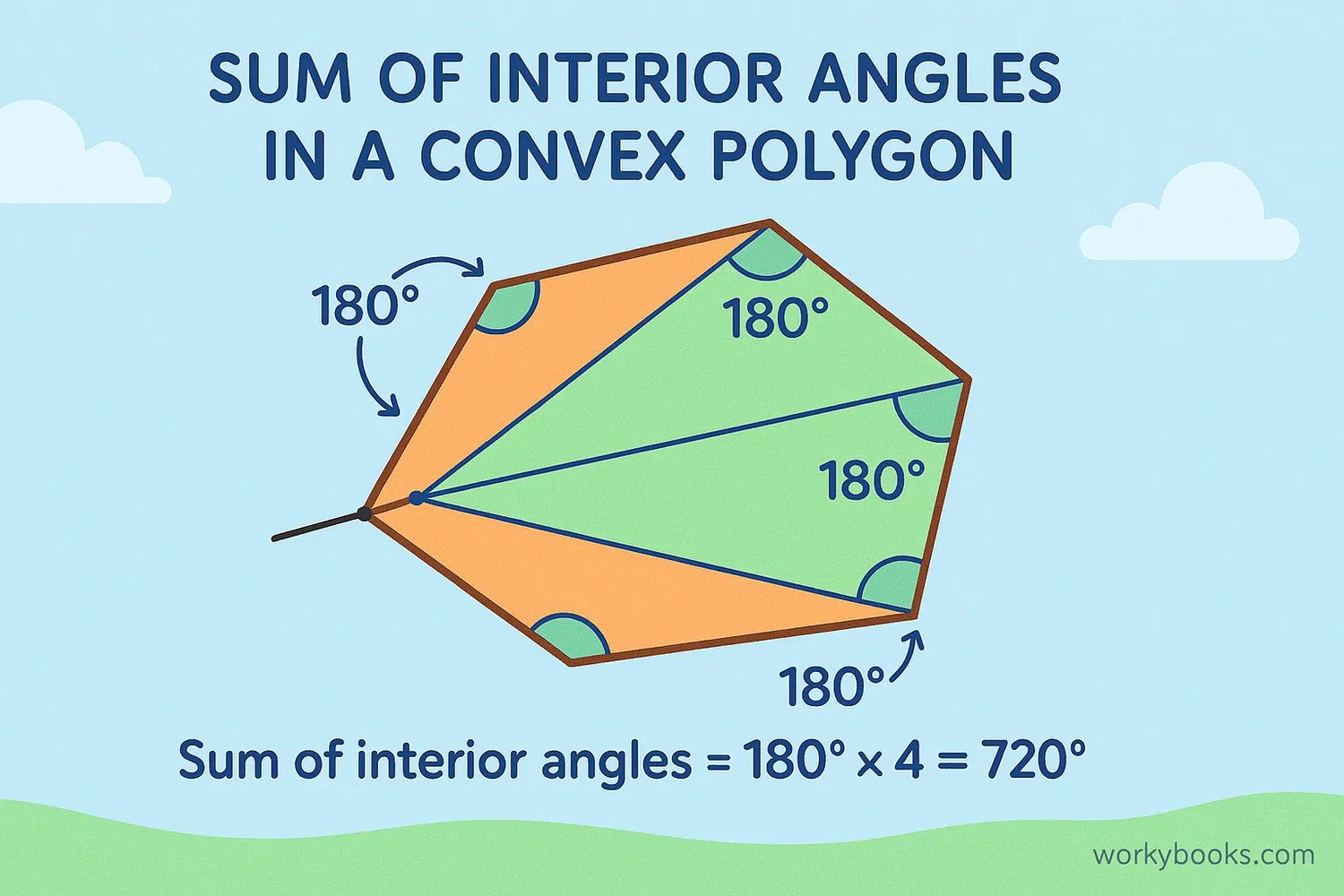
One special property of convex polygons is that we can calculate the sum of all interior angles using a simple formula:
Formula for Interior Angle Sum
Where S is the sum of interior angles and n is the number of sides
For a triangle (3 sides): (3-2) × 180° = 1 × 180° = 180°
For a quadrilateral (4 sides): (4-2) × 180° = 2 × 180° = 360°
For a pentagon (5 sides): (5-2) × 180° = 3 × 180° = 540°
This formula works for all convex polygons and even for concave polygons too!
Remember
For regular convex polygons, you can find each interior angle by dividing the sum by the number of angles: Interior Angle = [(n-2) × 180°] / n
Diagonals in Convex Polygons
A diagonal is a line segment connecting two non-adjacent vertices (corners) of a polygon. In convex polygons:
1. All diagonals stay inside: Unlike concave polygons, every diagonal of a convex polygon lies completely within the shape.
2. Number of diagonals: We can calculate how many diagonals a convex polygon has using this formula:
Formula for Number of Diagonals
Where D is the number of diagonals and n is the number of sides
For a quadrilateral (4 sides): 4(4-3)/2 = 4×1/2 = 2 diagonals
For a pentagon (5 sides): 5(5-3)/2 = 5×2/2 = 5 diagonals
For a hexagon (6 sides): 6(6-3)/2 = 6×3/2 = 9 diagonals
Convex Polygon Quiz
Test your knowledge about convex polygons with this 5-question quiz:
Frequently Asked Questions
Here are answers to common questions about convex polygons:
Polygon Trivia
Discover interesting facts about polygons and geometry:
Ancient Polygons
The ancient Greeks were the first to systematically study polygons around 300 BCE. Euclid's "Elements" contained detailed information about polygons that is still valid today.
Nature's Polygons
Honeybees build their hives with hexagonal cells because this shape uses the least amount of wax while storing the most honey - a perfect example of convex polygons in nature!
Circle of Polygons
As you add more sides to a regular convex polygon, it starts to look more and more like a circle. With infinite sides, it would be a perfect circle!
Architectural Polygons
The Pentagon building in Washington D.C. is one of the world's largest convex pentagons, covering 6.5 million square feet with five equal sides and five interior angles.





