Corresponding Angles - Definition, Examples, Quiz, FAQ, Trivia
Learn how angles relate to each other with easy explanations, examples, and practice activities
What Are Corresponding Angles?
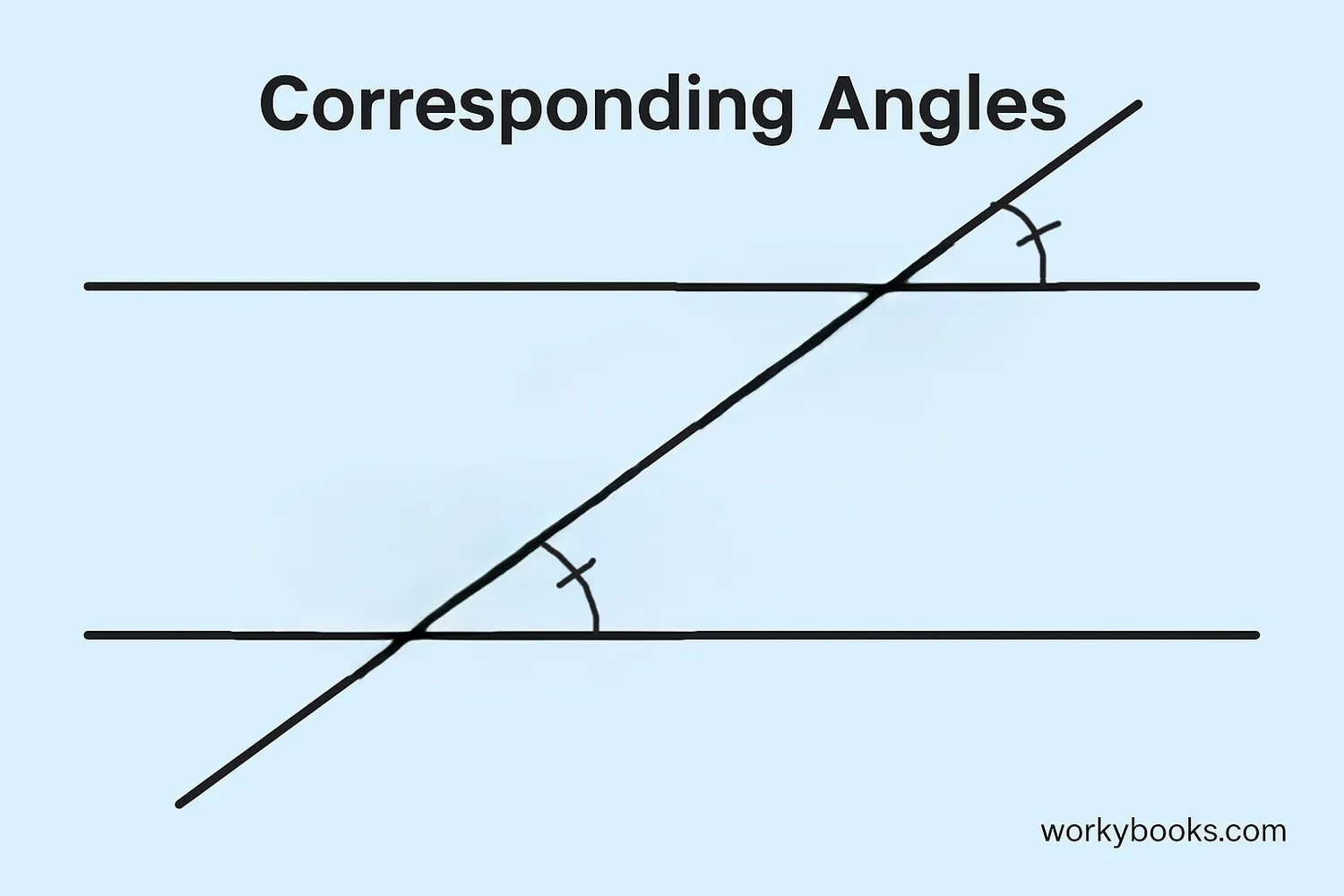
Corresponding angles are pairs of angles that are in matching positions at the intersections where a straight line crosses two other lines. This straight line that crosses the other lines is called a transversal.
Imagine two train tracks (parallel lines) and a road crossing them (transversal). The angles that are in the same position at each crossing are corresponding angles.
When the two lines are parallel, corresponding angles are always equal. But when the lines are not parallel, the corresponding angles are not equal.
Key Concept
Corresponding angles are formed when a transversal crosses two lines. They are on the same side of the transversal and in the same relative position.
Corresponding Angles Theorem
The Corresponding Angles Theorem states that when two parallel lines are crossed by a transversal, the corresponding angles are equal.
Corresponding Angles Postulate
This is a fundamental rule in geometry that helps us solve many angle problems.
If one corresponding angle measures 45°, the other corresponding angle will also measure 45° when the lines are parallel.
This relationship helps us find unknown angle measures in geometric figures and real-world applications like construction and design.
Remember
The Corresponding Angles Theorem only works when the lines are parallel. If lines aren't parallel, the angles won't be equal!
Corresponding Angles in Non-Parallel Lines
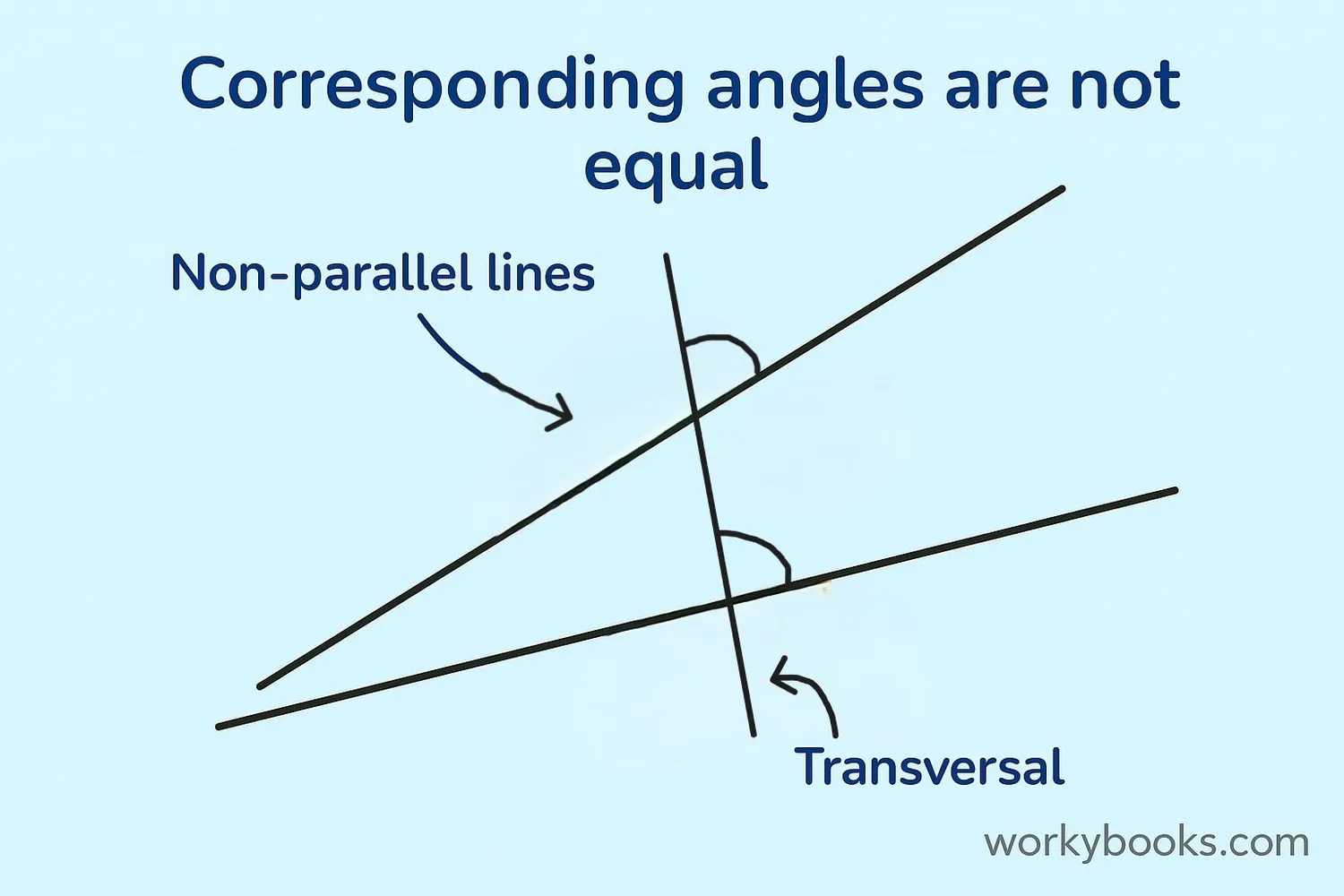
When a transversal crosses two lines that are not parallel, the corresponding angles are not equal.
In this case, the angles in matching positions will have different measurements. This is an important distinction because it helps us determine if lines are parallel or not.
If we measure the corresponding angles and find they are equal, we can conclude that the lines are parallel. If they're not equal, the lines are not parallel.
This relationship is useful in many real-world situations, like checking if walls are parallel in construction or if railroad tracks are properly aligned.
Real-World Application
Carpenters use the corresponding angles principle to ensure walls are parallel when building houses.
Examples of Corresponding Angles
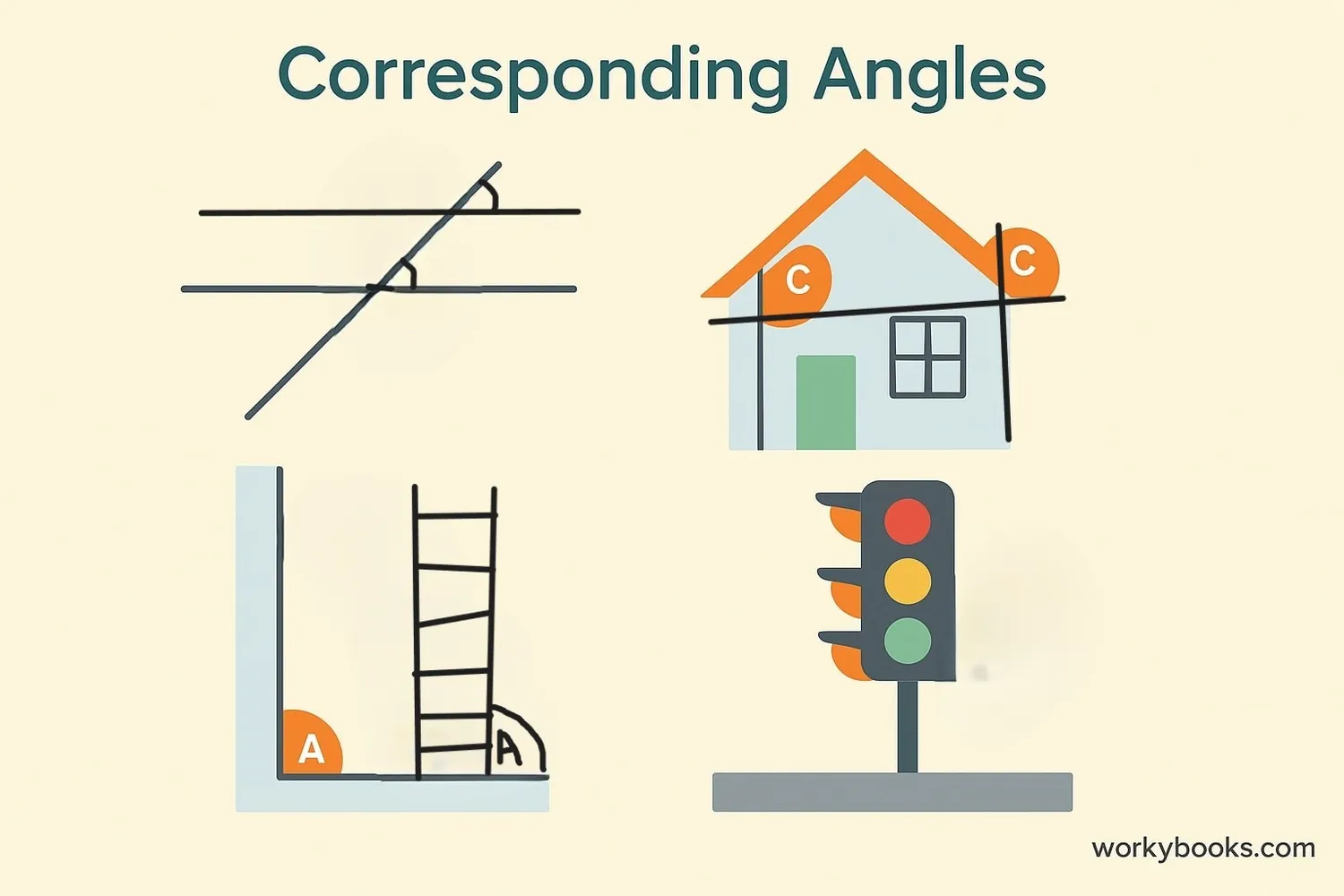
Let's look at some examples to understand corresponding angles better:
Example 1: In a rectangle, opposite sides are parallel. When we draw a diagonal (transversal), the corresponding angles formed are equal.
Example 2: In the letter "Z", the top and bottom lines are parallel. The diagonal line creates corresponding angles that are equal.
Example 3: On a soccer field, the parallel lines of the penalty area create corresponding angles with the diagonal lines.
Example 4: If two corresponding angles measure 65° and 65°, the lines are parallel. If one measures 65° and the other measures 70°, the lines are not parallel.
Practice Tip
Look for the letter "F" in different orientations to identify corresponding angles - they form the shape of an F!
Practice Quiz
Test your understanding of corresponding angles with these practice questions:
Frequently Asked Questions
Here are answers to common questions about corresponding angles:
Geometry Trivia
Discover interesting facts about angles and geometry:
Ancient Angle Knowledge
The concept of angles dates back to ancient Babylonian astronomers who divided circles into 360 degrees around 1800 BC. This system is still used today!
Angles in Nature
Honeybees build their honeycombs with perfect hexagonal shapes that form precise 120° angles. This efficient design uses the least amount of wax to store the most honey.
Architectural Angles
The famous Leaning Tower of Pisa leans at an angle of about 4 degrees. Engineers used angle relationships to stabilize it and prevent collapse.
Perfect Right Angle
The most precisely measured right angle is in the LIGO observatory, where mirrors are aligned at exactly 90 degrees to detect gravitational waves from space.





