CPCTC - Corresponding Parts of Congruent Triangles are Congruent - Definition, Examples, Quiz, FAQ, Trivia
Learn how to use CPCTC to prove that matching parts of triangles are equal
What is CPCTC?
CPCTC stands for Corresponding Parts of Congruent Triangles are Congruent. This is a very important rule in geometry that helps us prove that different parts of triangles are equal to each other.
Think of it like this: If you have two identical triangles (they match perfectly when you place one on top of the other), then all their matching parts will be equal. The sides that match will be the same length, and the angles that match will have the same measurement.
We use CPCTC after we've already proved that two triangles are congruent. Once we know the triangles are congruent, we can say that any of their corresponding parts (sides or angles) are also congruent.
Key Concept
CPCTC is only used AFTER you have proved that two triangles are congruent. It's the final step that lets you say that specific parts are equal.
Triangle Congruence Conditions

Before we can use CPCTC, we need to prove that two triangles are congruent. There are five main ways to prove that triangles are congruent:
SSS - Side-Side-Side
If all three sides of one triangle are equal to all three sides of another triangle, then the triangles are congruent.
SAS - Side-Angle-Side
If two sides and the included angle (the angle between them) of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.
ASA - Angle-Side-Angle
If two angles and the included side (the side between them) of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
AAS - Angle-Angle-Side
If two angles and a non-included side (a side not between them) of one triangle are equal to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.
HL - Hypotenuse-Leg
For right triangles only: If the hypotenuse and one leg of one right triangle are equal to the hypotenuse and one leg of another right triangle, then the triangles are congruent.
Remember
You must use one of these five methods to prove triangles congruent before you can use CPCTC to prove that their corresponding parts are equal.
How to Use CPCTC in Proofs
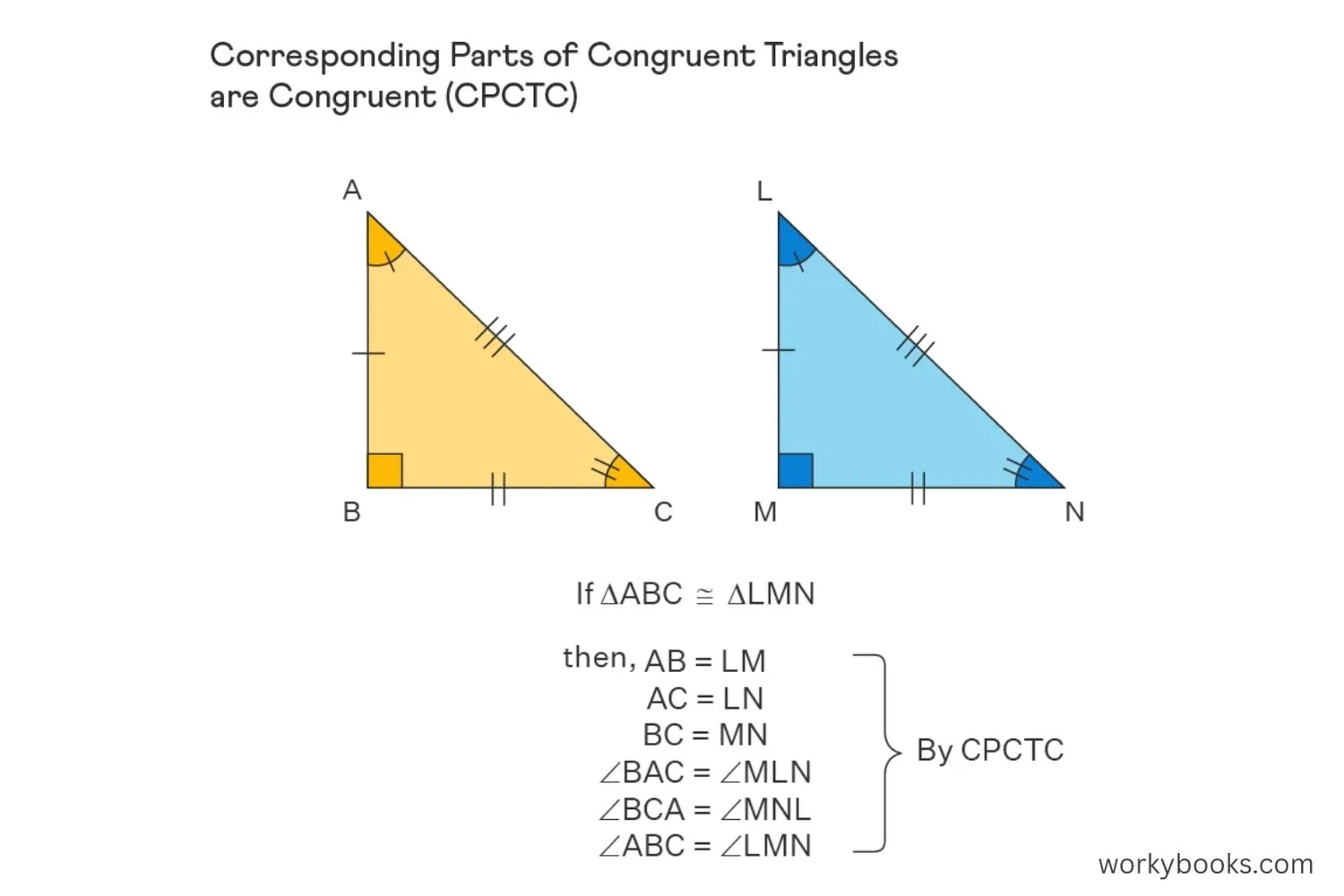
Using CPCTC in a proof involves several steps. Let's look at how it works:
Step 1: Identify the two triangles you want to prove congruent.
Step 2: Find three pairs of equal parts (sides or angles) using given information or properties.
Step 3: Prove the triangles are congruent using one of the five methods (SSS, SAS, ASA, AAS, or HL).
Step 4: Once you've proved the triangles congruent, use CPCTC to prove that other corresponding parts are congruent.
Proof Tip
CPCTC is usually the last step in a proof. It allows you to conclude that specific parts are equal once you've established that the triangles are congruent.
CPCTC Examples
Let's look at some examples of how CPCTC works in real geometry problems:
Example 1: Proving Angles Equal
Given: △ABC and △DEF where AB = DE, BC = EF, and AC = DF
Prove: ∠A = ∠D
Solution:
1. AB = DE (Given)
2. BC = EF (Given)
3. AC = DF (Given)
4. ∴ △ABC ≅ △DEF (SSS)
5. ∴ ∠A = ∠D (CPCTC)
Example 2: Proving Sides Equal
Given: M is midpoint of AB, ∠A = ∠B
Prove: AM = MB
Solution:
1. M is midpoint of AB (Given) → AM = MB (Definition of midpoint)
2. ∠A = ∠B (Given)
3. AB = AB (Reflexive property)
4. △AMC ≅ △BMC (SAS)
5. ∴ AM = MB (CPCTC)
Practice Tip
Always look for triangles that share a side or angle. This common element often helps prove congruence.
CPCTC Practice Quiz
Test your understanding of CPCTC with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about CPCTC:
Geometry Trivia
Discover interesting facts about geometry and triangles:
Ancient Geometry
Geometry dates back to ancient Egypt around 3000 BC, where it was used to survey land after Nile River floods. The word "geometry" comes from Greek words meaning "earth measurement."
Triangles in Nature
Triangles are the strongest geometric shape, which is why they're used in bridges and roof supports. Bees use triangles in their honeycombs because this shape uses the least amount of wax while storing the most honey.
Triangles in Space
NASA uses triangle congruence principles in spacecraft design and navigation. The Mars rovers use geometric calculations to navigate the Martian terrain and position their instruments accurately.
Largest Triangle
The largest triangle ever created was part of an art project in the Nevada desert. It had sides measuring 1.2 miles each and was visible from space! That's about 6,336 feet per side.





