Cube Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn about perfect cubes, cube roots, and their properties with visual examples and quizzes
What is a Cube Number?
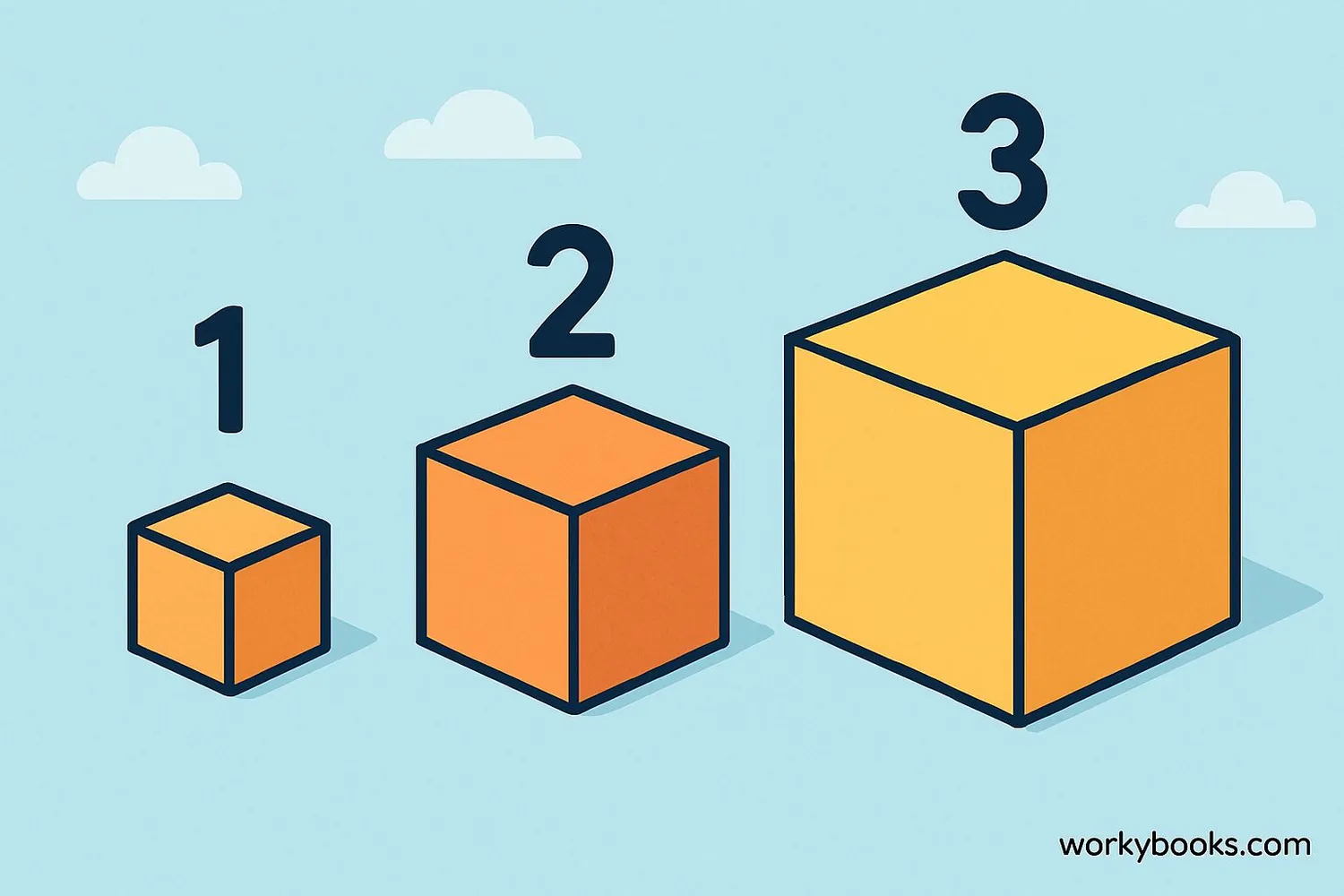
A cube number (or a perfect cube) is a number you get when you multiply a whole number by itself three times. It's like building a cube with blocks!
For example:
• 2 × 2 × 2 = 8, so 8 is a cube number
• 3 × 3 × 3 = 27, so 27 is a cube number
We call them "cube numbers" because they represent the volume of a cube with whole number side lengths. Imagine building a cube with blocks - a 2x2x2 cube would have 8 blocks, a 3x3x3 cube would have 27 blocks.
Cube Number Formula
Where n is any whole number
Key Concept
Cube numbers are the result of multiplying a whole number by itself three times. They're called "perfect cubes."
How to Find Cube Numbers
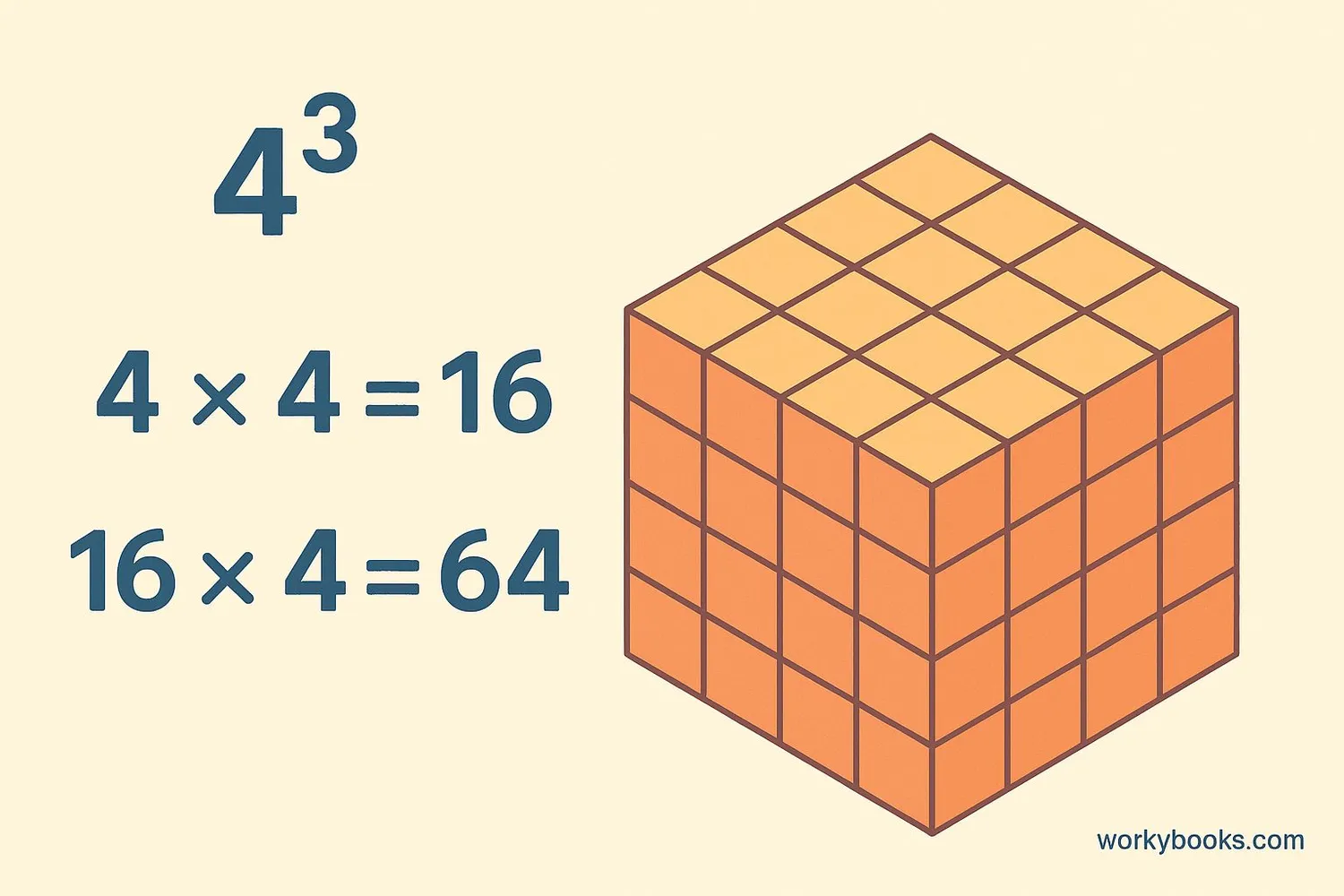
Finding cube numbers is simple! Just follow these steps:
1. Choose any whole number (like 1, 2, 3, 4...)
2. Multiply that number by itself
3. Multiply the result by the original number again
Let's practice with an example:
Example: Find the cube of 4
Step 1: Start with the number → 4
Step 2: Multiply 4 × 4 → 16
Step 3: Multiply 16 × 4 → 64
So 4³ = 64. That means 64 is a cube number!
Remember
Cube numbers grow very quickly! 10³ = 1,000 and 20³ = 8,000.
List of Cube Numbers

Here are the first 15 cube numbers. Notice how they grow quickly as the numbers get larger!
Interesting Pattern
Look at the last digits: 1, 8, 7, 4, 5, 6, 3, 2, 9, 0 and then they repeat! Cube numbers have this repeating pattern in their last digit.
Cube Roots
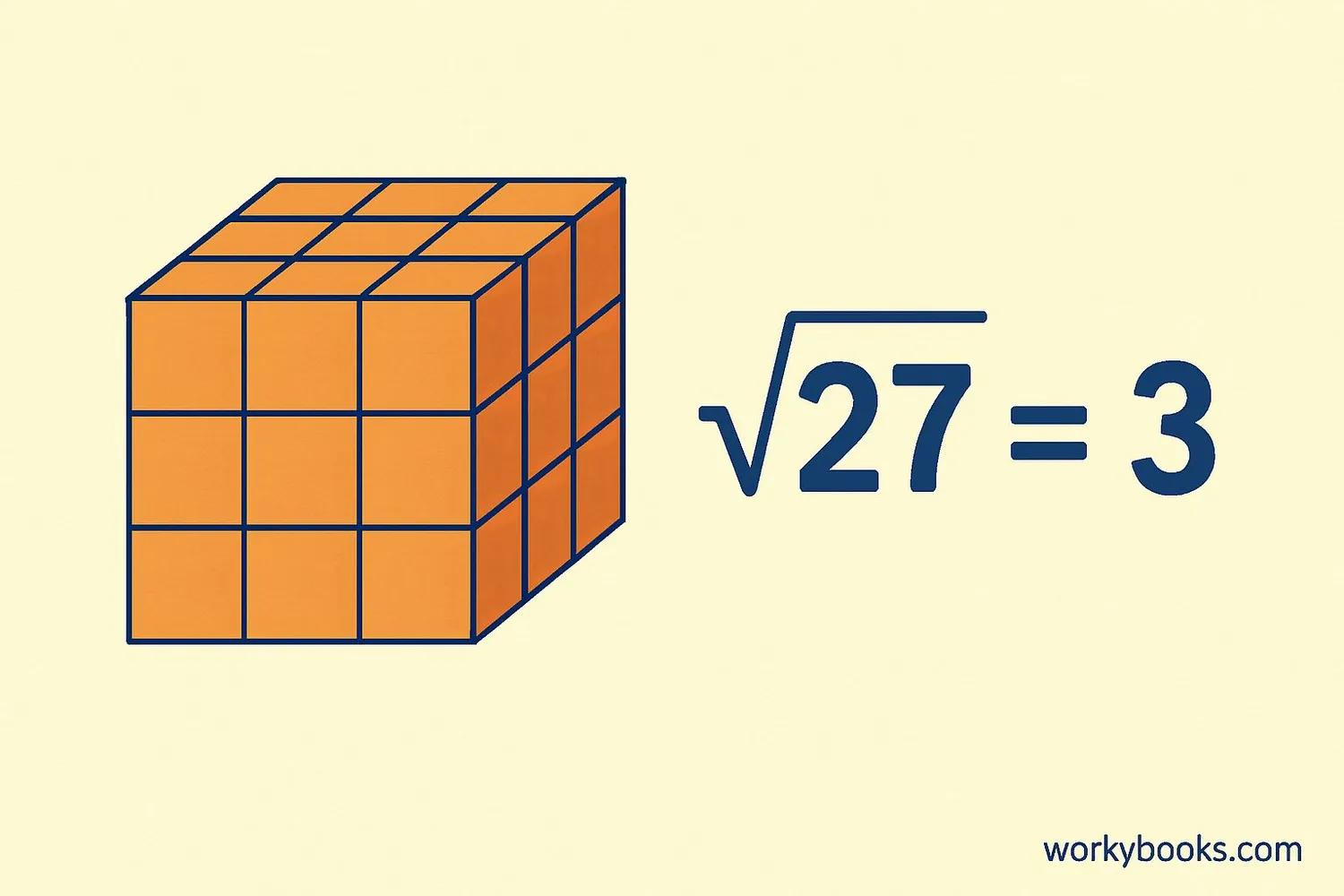
The cube root is the opposite of cubing a number. It answers the question: "What number multiplied by itself three times gives this cube number?"
We use the special symbol ∛ to show cube roots.
Examples:
• ∛8 = 2 because 2 × 2 × 2 = 8
• ∛27 = 3 because 3 × 3 × 3 = 27
• ∛64 = 4 because 4 × 4 × 4 = 64
Finding cube roots helps us work backwards from a cube number to the original number. It's like unpacking a cube to find how long each side was!
Cube Root Definition
Where a is a perfect cube and b is a whole number
Remember
Every positive number has one real cube root. Unlike square roots, cube roots can also be found for negative numbers!
Properties of Cube Numbers

Cube numbers have some interesting properties that make them special:
1. Even and Odd Cubes:
• The cube of an even number is even (2³=8, 4³=64)
• The cube of an odd number is odd (3³=27, 5³=125)
2. Last Digit Patterns:
The last digit of a cube number follows a pattern that repeats every 10 numbers. The possible last digits are 0, 1, 8, 7, 4, 5, 6, 3, 2, 9.
3. Sum of Consecutive Odd Numbers:
Any cube number can be expressed as the sum of consecutive odd numbers:
8 = 3 + 5
27 = 7 + 9 + 11
64 = 13 + 15 + 17 + 19
4. Minimum Number of Factors:
Every cube number has at least 4 factors. For example, 8 has factors 1, 2, 4, 8.
Interesting Fact
The sum of the cubes of the first n natural numbers is equal to the square of their sum!
1³ + 2³ + 3³ + ... + n³ = (1 + 2 + 3 + ... + n)²
Cube Numbers Practice Quiz
Test your understanding of cube numbers with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about cube numbers:
Math Trivia
Discover interesting facts about cube numbers:
Ancient Cube Calculations
Ancient Babylonians calculated cube roots as early as 1800 BCE! They used clay tablets with cuneiform writing to solve cubic equations.
Rubik's Cube
The Rubik's Cube has 43,252,003,274,489,856,000 possible configurations. That's 43 quintillion - much larger than any cube number!
The Smallest Cube
The smallest cube that can be divided into smaller cubes of different sizes is the 112×112×112 cube. It can be divided into 50 smaller cubes of different integer sizes.
Cubic Growth
Cube numbers grow much faster than square numbers. While 10² is 100, 10³ is 1,000. At 100, the square is 10,000 but the cube is 1,000,000 - one million!





