Cube Root - Definition, Examples, Quiz, FAQ, Trivia
Learn about cube roots with simple explanations, visual examples, and practice activities
What is a Cube Root?

A cube root is a special number that, when multiplied by itself three times, gives the original number.
Think about building a cube with small blocks. If you have 8 small blocks, you can build a 2x2x2 cube. So the cube root of 8 is 2. If you have 27 blocks, you can build a 3x3x3 cube, so the cube root of 27 is 3.
Example: What's the cube root of 125? It's 5 because 5 × 5 × 5 = 125.
Key Concept
The cube root of a number answers the question: "What number multiplied by itself three times equals this number?"
Cube Root Symbol
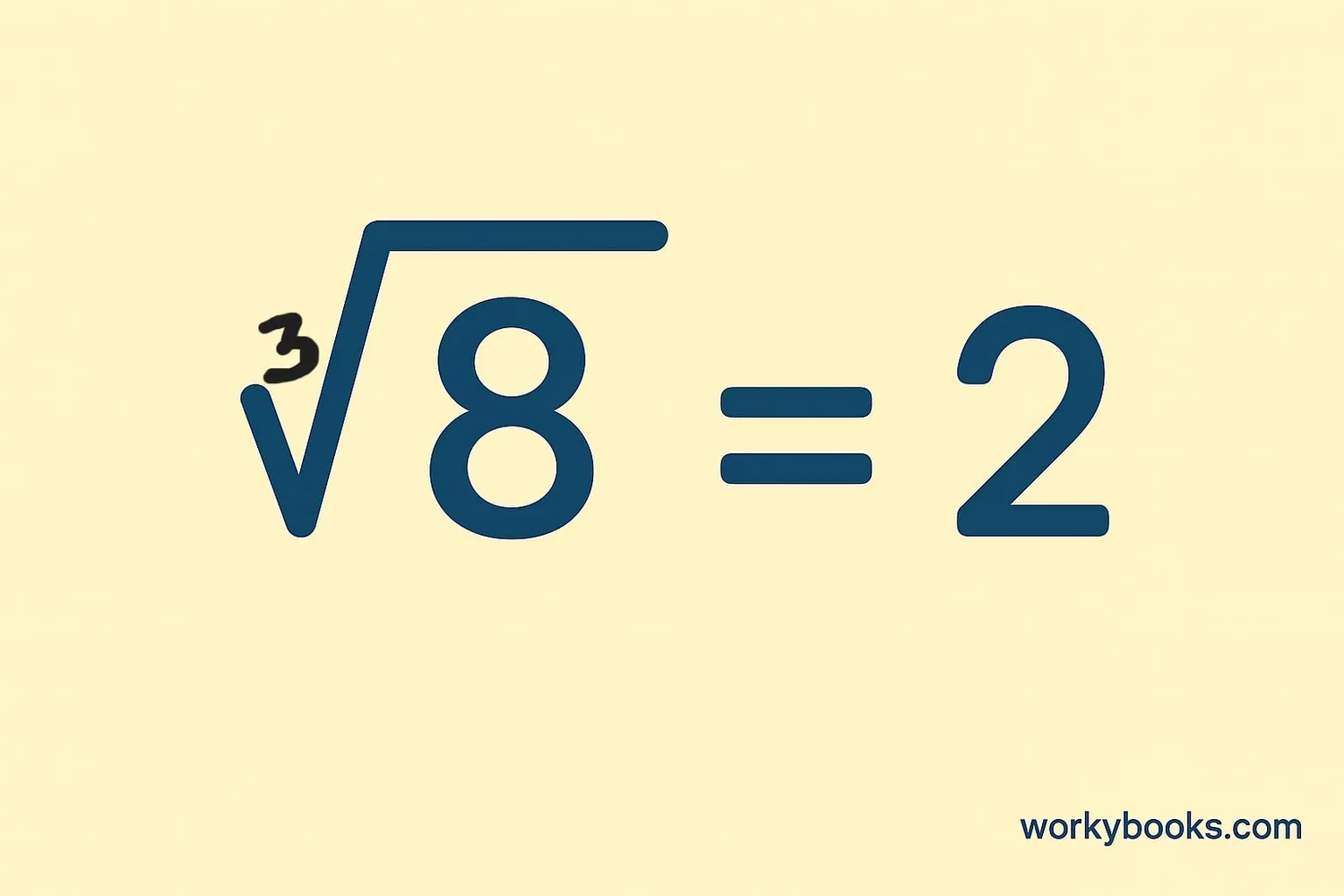
The cube root symbol looks like this: ∛
It's a special symbol that means "cube root." You write it before a number to show you're finding its cube root.
Examples:
∛8 = 2 (because 2 × 2 × 2 = 8)
∛27 = 3 (because 3 × 3 × 3 = 27)
∛64 = 4 (because 4 × 4 × 4 = 64)
The small 3 in the symbol tells us we're finding the cube root, not the square root.
Cube Root Formula
This formula shows the relationship between a number and its cube root.
How to Find Cube Roots
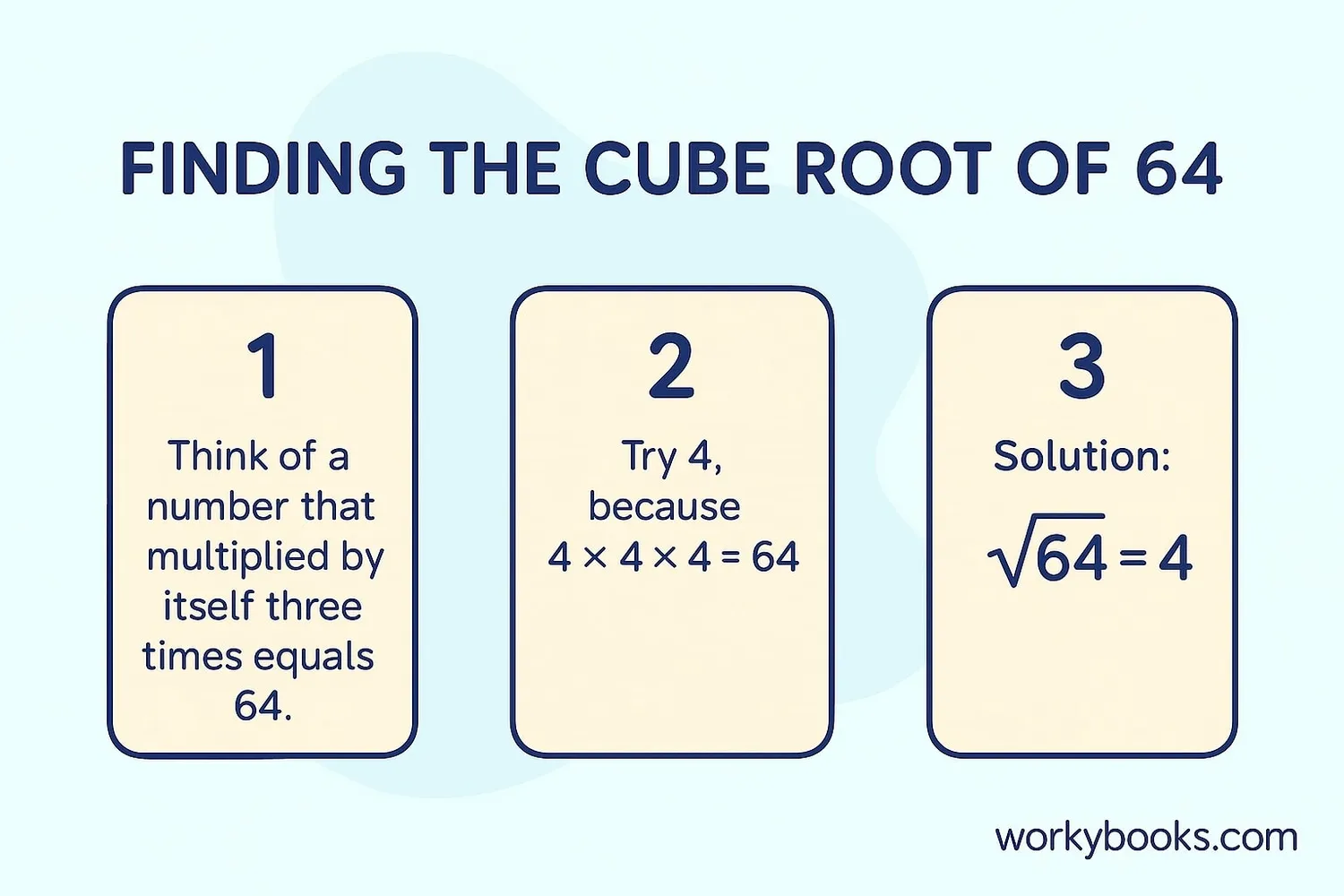
Finding cube roots is easier when you know some perfect cubes. Here's how to do it:
Step 1: Learn the first few perfect cubes:
- 1³ = 1 × 1 × 1 = 1
- 2³ = 2 × 2 × 2 = 8
- 3³ = 3 × 3 × 3 = 27
- 4³ = 4 × 4 × 4 = 64
- 5³ = 5 × 5 × 5 = 125
- 6³ = 6 × 6 × 6 = 216
- 7³ = 7 × 7 × 7 = 343
- 8³ = 8 × 8 × 8 = 512
- 9³ = 9 × 9 × 9 = 729
- 10³ = 10 × 10 × 10 = 1000
Step 3: For numbers that aren't perfect cubes, you can estimate. For example, ∛50 is between 3 and 4 because 3³=27 and 4³=64.
Remember
Cube roots of negative numbers are also negative. For example, ∛(-8) = -2 because (-2) × (-2) × (-2) = -8.
Cube Root Examples
Let's look at some common cube roots:
| Number | Cube Root | Explanation |
|---|---|---|
| 1 | 1 | 1 × 1 × 1 = 1 |
| 8 | 2 | 2 × 2 × 2 = 8 |
| 27 | 3 | 3 × 3 × 3 = 27 |
| 64 | 4 | 4 × 4 × 4 = 64 |
| 125 | 5 | 5 × 5 × 5 = 125 |
| 216 | 6 | 6 × 6 × 6 = 216 |
| 343 | 7 | 7 × 7 × 7 = 343 |
| 512 | 8 | 8 × 8 × 8 = 512 |
| 729 | 9 | 9 × 9 × 9 = 729 |
| 1000 | 10 | 10 × 10 × 10 = 1000 |
Real-World Application
Cube roots help us solve problems like finding the side length of a cube when we know its volume.
Cube Root Practice Quiz
Test your understanding with these practice questions. Choose the correct answer for each.
Frequently Asked Questions
Here are answers to common questions about cube roots:
Math Trivia
Discover interesting facts about cube roots and mathematics:
Ancient Calculations
The concept of cube roots dates back to ancient Babylonian mathematics around 1800 BCE. Clay tablets show that Babylonians had methods for approximating cube roots.
Real-World Applications
Cube roots are used in many real-world applications, including calculating the size of objects, understanding volume relationships, and in physics for wave functions.
Cube Root of Large Numbers
The cube root of 1,000 is 10. The cube root of 1,000,000 is 100. Notice the pattern? For every three zeros added to a number, the cube root gains one zero.
Largest Perfect Cube
The largest perfect cube most calculators can display is 999,999,999,999,999. Its cube root is 99,999.99999999999 - almost 100,000!





