Cube Root of 64 - Definition, Examples, Quiz, FAQ, Trivia
Learn what cube roots are, how to find them, and solve fun problems with visual examples
What is Cube Root?
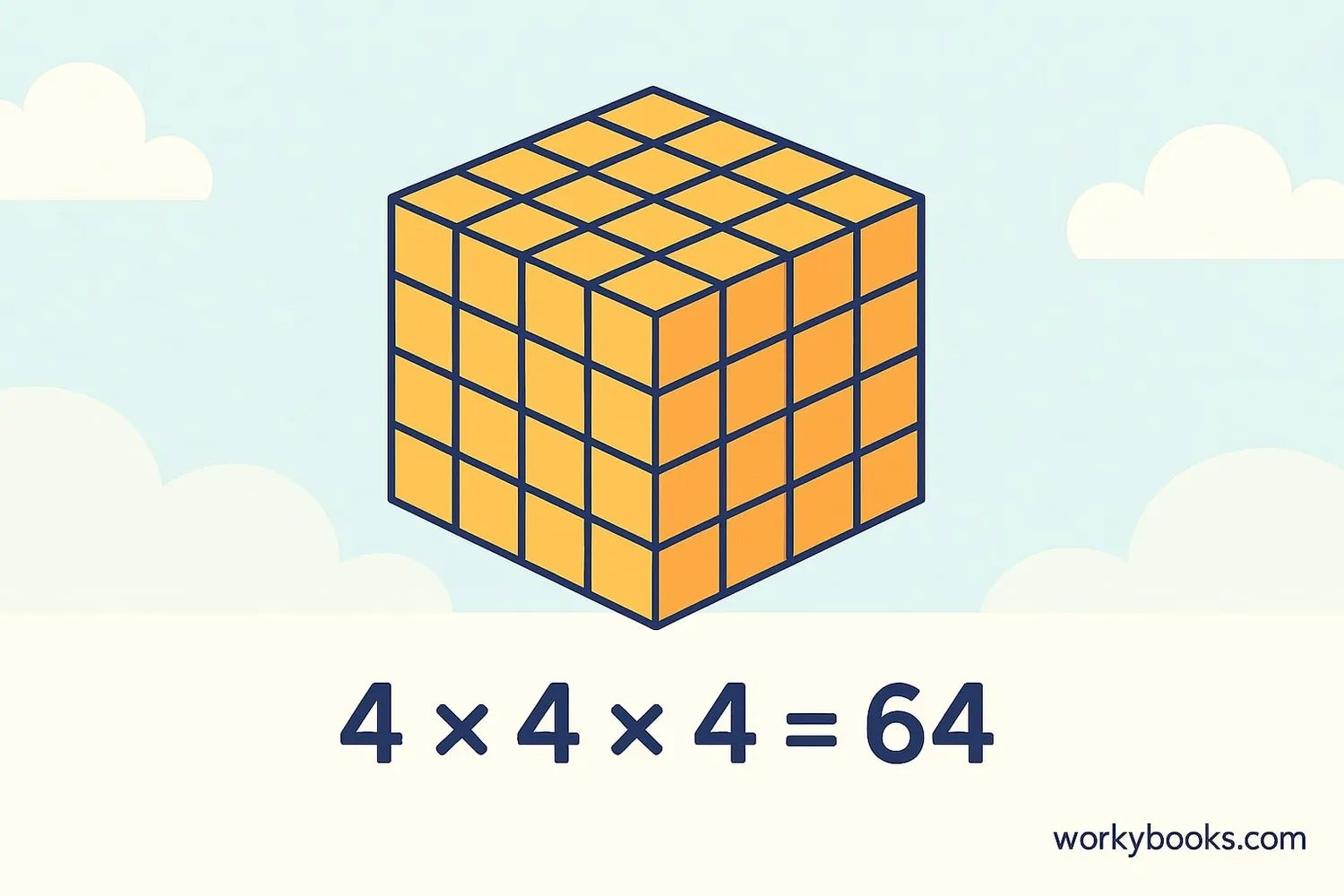
A cube root is a special number that, when multiplied by itself three times, gives the original number.
It's like asking: "What number cubed equals this number?" The cube root symbol is ∛.
For example, the cube root of 64 is 4 because:
4 × 4 × 4 = 64
We write this as: ∛64 = 4
Think of it like building a cube with blocks. If you have 64 small blocks, you can arrange them into a perfect cube that's 4 blocks wide, 4 blocks tall, and 4 blocks deep.
Key Concept
The cube root of a number n is the value that satisfies the equation: ∛n × ∛n × ∛n = n
Finding the Cube Root of 64
There are two main ways to find the cube root of 64:
1. Prime Factorization Method:
Step 1: Factor 64 into prime numbers: 64 = 2 × 2 × 2 × 2 × 2 × 2
Step 2: Group the factors in sets of three: (2 × 2 × 2) and (2 × 2 × 2)
Step 3: Take one factor from each group: 2 × 2 = 4
Step 4: So ∛64 = 4
2. Using the Cube Root Formula:
We know that 4³ = 4 × 4 × 4 = 16 × 4 = 64
Therefore, ∛64 = 4
Cube Root Formula
Because 4 × 4 × 4 = 64
Remember
Cube root is the opposite operation of cubing a number. If 4³ = 64, then ∛64 = 4.
Is 64 a Perfect Cube?
Visual representation of a 4×4 cube layer
Yes, 64 is a perfect cube! A perfect cube is a number that can be expressed as the cube of an integer.
Since 4 is an integer (a whole number) and 4 × 4 × 4 = 64, 64 is a perfect cube.
Other perfect cubes:
1³ = 1 (∛1 = 1)
2³ = 8 (∛8 = 2)
3³ = 27 (∛27 = 3)
4³ = 64 (∛64 = 4)
5³ = 125 (∛125 = 5)
Perfect cubes make neat cube shapes when represented with blocks, with equal sides and no leftover blocks.
Cube Tip
Numbers like 64 that are perfect cubes have whole number cube roots.
Cube Root of Negative Numbers
We can also find cube roots of negative numbers! The cube root of a negative number is negative.
For example, the cube root of -64 is -4 because:
(-4) × (-4) × (-4) = -64
Let's break it down:
Step 1: (-4) × (-4) = 16 (negative × negative = positive)
Step 2: 16 × (-4) = -64 (positive × negative = negative)
So we write: ∛(-64) = -4
This is different from square roots, where we can't have real square roots of negative numbers. But with cube roots, it works!
Negative Cube Root Formula
Because (-4) × (-4) × (-4) = -64
Cube Roots of Fractions and Decimals
Cube roots work with fractions and decimals too! Here are some examples:
1. Cube Root of 64/125:
∛(64/125) = ∛64 / ∛125 = 4/5 = 0.8
2. Cube Root of 0.064:
0.064 = 64/1000
∛(64/1000) = ∛64 / ∛1000 = 4/10 = 0.4
3. Cube Root of -64/343:
∛(-64/343) = ∛(-64) / ∛343 = -4/7 ≈ -0.571
Remember: When finding the cube root of a fraction, you can find the cube root of the numerator and the cube root of the denominator separately.
Fraction Tip
∛(a/b) = ∛a / ∛b for any numbers a and b (as long as b ≠ 0)
Cube Root Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about cube roots:
Math Trivia
Discover interesting facts about cube roots and numbers:
Ancient Cube Roots
The concept of cube roots dates back to ancient Babylonian mathematics around 1800 BCE. Clay tablets show they had methods for calculating cube roots!
Cube Roots in Nature
Cube roots appear in science when dealing with volume. For example, if you know the volume of a cube, the cube root gives you the length of its sides.
Cube Root Symbol
The cube root symbol ∛ was first used by mathematician Christoph Rudolff in 1525. The check mark part comes from the letter "r" for "radix" (root).
Largest Cube Root
The largest cube root calculated by hand was ∛999,999,999 = 999.999999 approximately. Computers can now calculate cube roots of enormous numbers!





