Decagon: The 10-Sided Shape - Definition, Examples, Quiz, FAQ, Trivia
Learn about decagons with easy explanations, properties, formulas, and interactive activities
What is a Decagon?
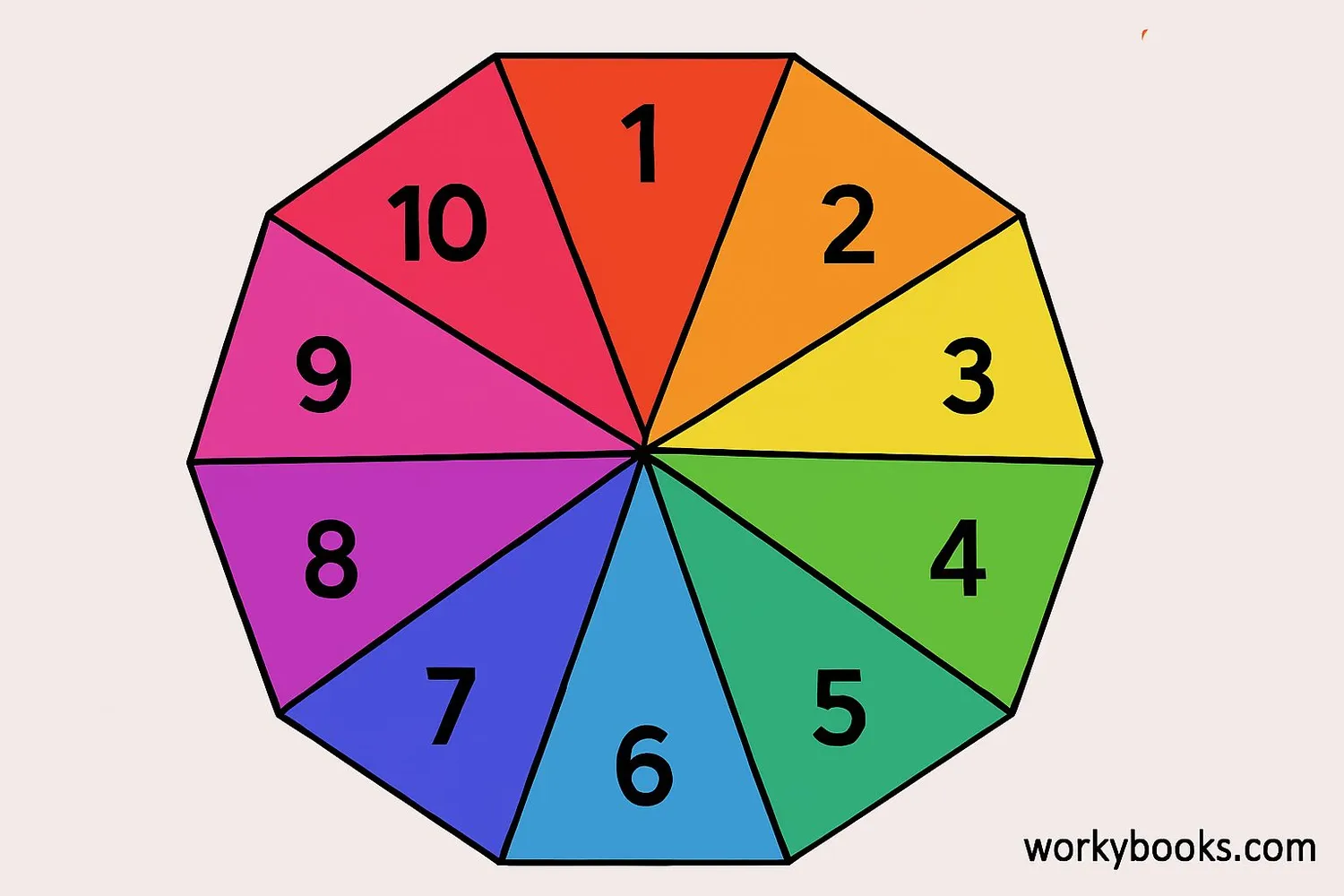
A decagon is a special shape in geometry with 10 sides and 10 angles. The word "decagon" comes from Greek words: "deka" meaning ten and "gonia" meaning angle.
Decagons can be found all around us! Some examples include:
- Stop signs (octagons are more common, but some signs use decagons)
- Certain coins and medallions
- Decorative tiles and patterns
- Some sports balls like soccer balls have pentagons and hexagons, but decagons appear in other designs
All decagons have these features:
- 10 straight sides
- 10 vertices (corners)
- 10 interior angles
- The sum of all interior angles is 1440 degrees
Key Concept
Decagon = 10 sides, 10 angles, and 10 vertices. The prefix "deca-" always means ten!
Regular Decagon Properties
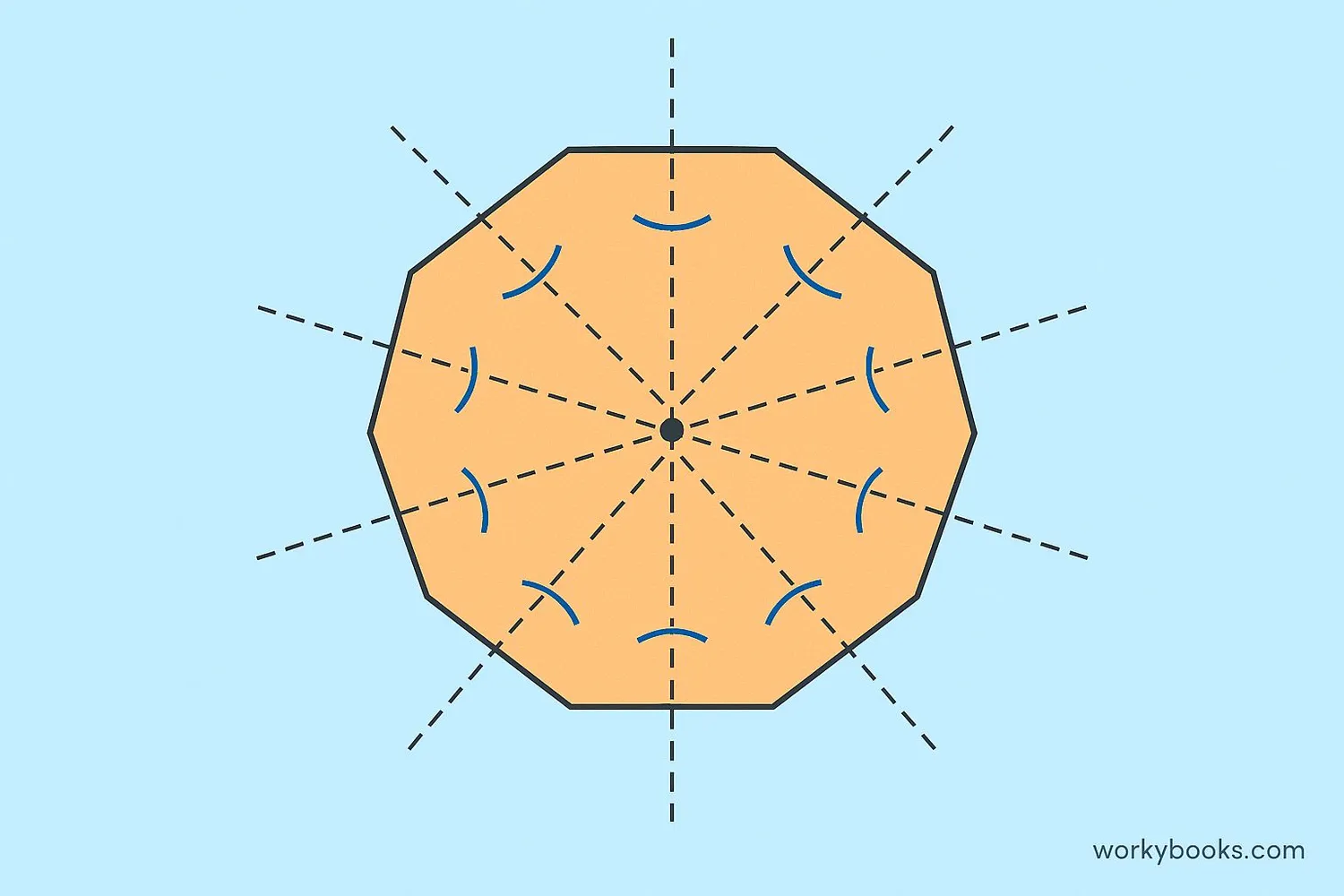
A regular decagon is special because all its sides are equal in length, and all its angles are equal in measure. This makes it symmetrical and balanced.
Properties of a regular decagon:
- All 10 sides are equal length
- All 10 interior angles measure 144° each
- It has 10 lines of symmetry
- It has rotational symmetry of order 10 (looks the same after 36° rotations)
- The exterior angles are each 36°
Regular decagons are particularly interesting because they have so many symmetrical properties. This makes them useful in design and architecture where balance and harmony are important.
Remember
In a regular decagon, every side is the same length and every angle is the same size!
| Shape | Number of Sides | Special Name |
|---|---|---|
| 3 sides | 3 | Triangle |
| 4 sides | 4 | Quadrilateral |
| 5 sides | 5 | Pentagon |
| 6 sides | 6 | Hexagon |
| 7 sides | 7 | Heptagon |
| 8 sides | 8 | Octagon |
| 9 sides | 9 | Nonagon |
| 10 sides | 10 | Decagon |
Interior Angles of a Decagon
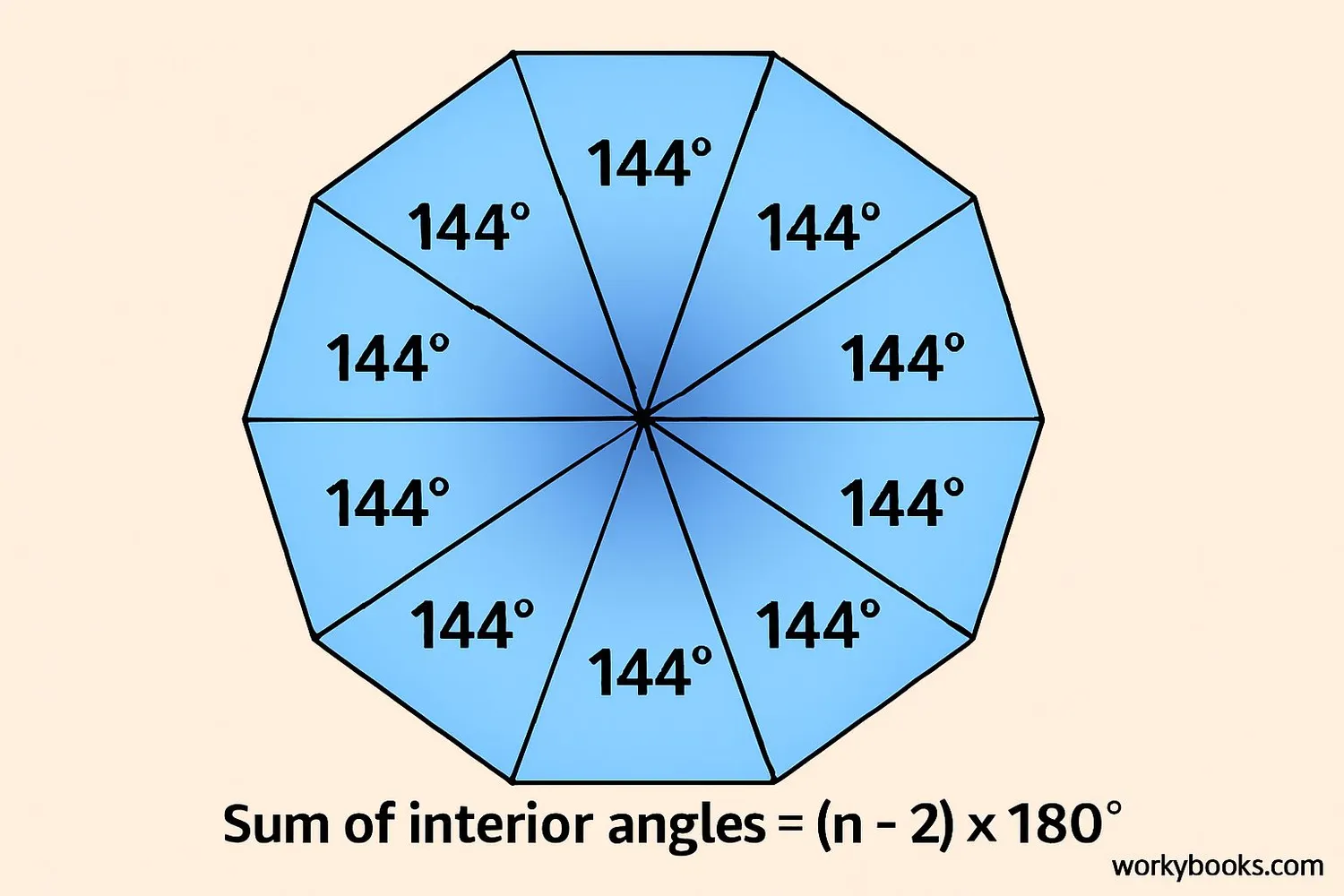
The angles inside a decagon are called interior angles. There are two important things to know about decagon angles:
Angle Sum Formula
Where n is the number of sides
Sum of interior angles = (10 - 2) × 180° = 8 × 180° = 1440°
In a regular decagon (where all angles are equal):
Each interior angle = 1440° ÷ 10 = 144°
Let's see how this works with an example:
Example: If 9 angles of a decagon measure 143° each, what is the measure of the tenth angle?
Solution:
Step 1: Total of 9 angles = 9 × 143° = 1287°
Step 2: Total for all 10 angles = 1440°
Step 3: Tenth angle = 1440° - 1287° = 153°
Angle Tip
For any polygon, the sum of interior angles = (number of sides - 2) × 180°
Perimeter of a Decagon
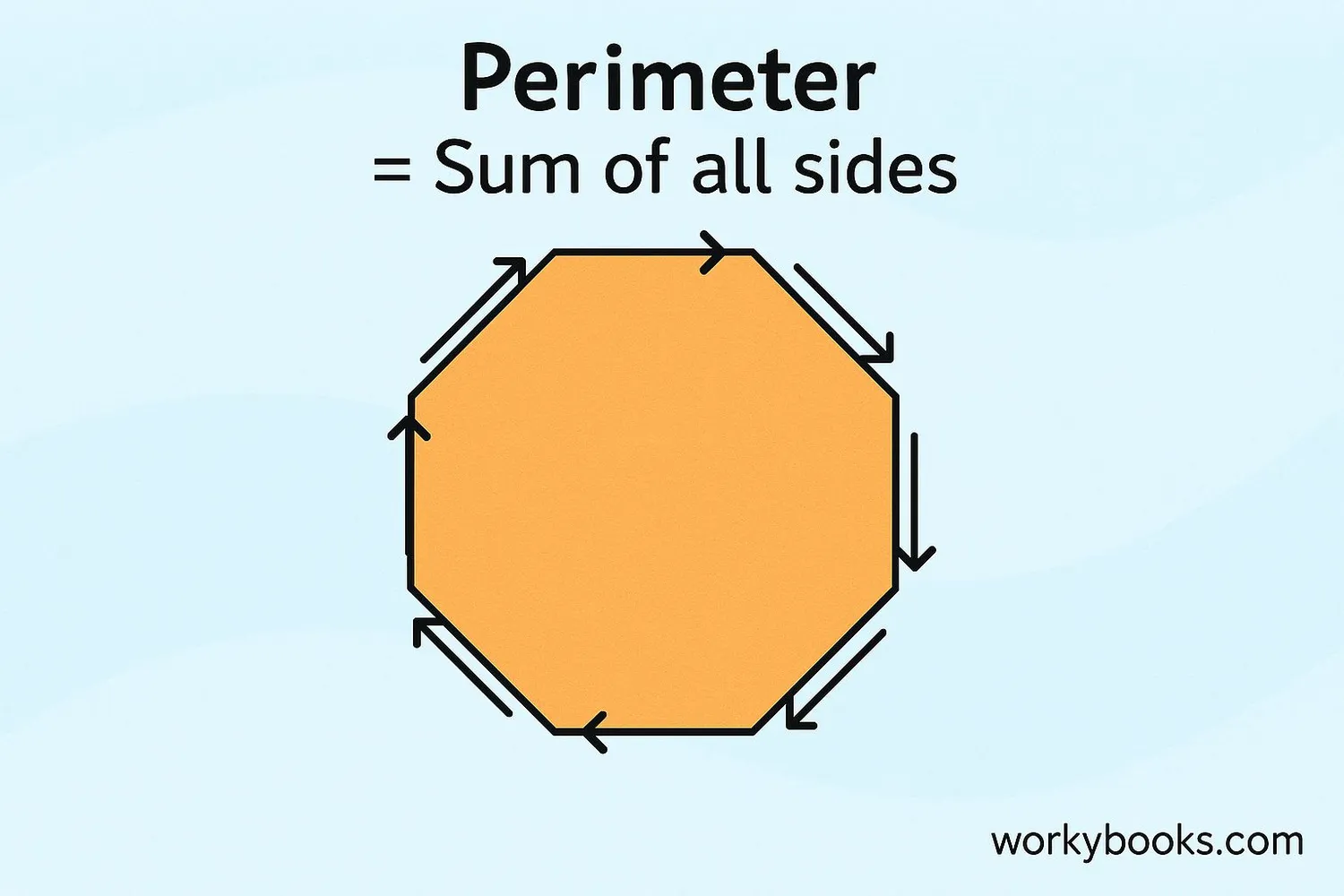
The perimeter of a decagon is the total distance around the shape - the sum of all its sides. It's like measuring how far you'd walk if you went around the entire shape.
Calculating perimeter is simple:
Perimeter Formula
Where s is the length of one side
Example: A regular decagon has sides that are 7 cm each. What is its perimeter?
Solution: Perimeter = 10 × 7 cm = 70 cm
For an irregular decagon (where sides may have different lengths):
Perimeter = side₁ + side₂ + side₃ + ... + side₁₀
Example: An irregular decagon has sides measuring: 5cm, 6cm, 5.5cm, 6.2cm, 5.8cm, 6cm, 5.3cm, 6.5cm, 5.7cm, 6.1cm. What is its perimeter?
Solution: Add all side lengths: 5 + 6 + 5.5 + 6.2 + 5.8 + 6 + 5.3 + 6.5 + 5.7 + 6.1 = 58.1 cm
Perimeter Tip
For regular polygons, perimeter = number of sides × side length. Easy!
Area of a Regular Decagon
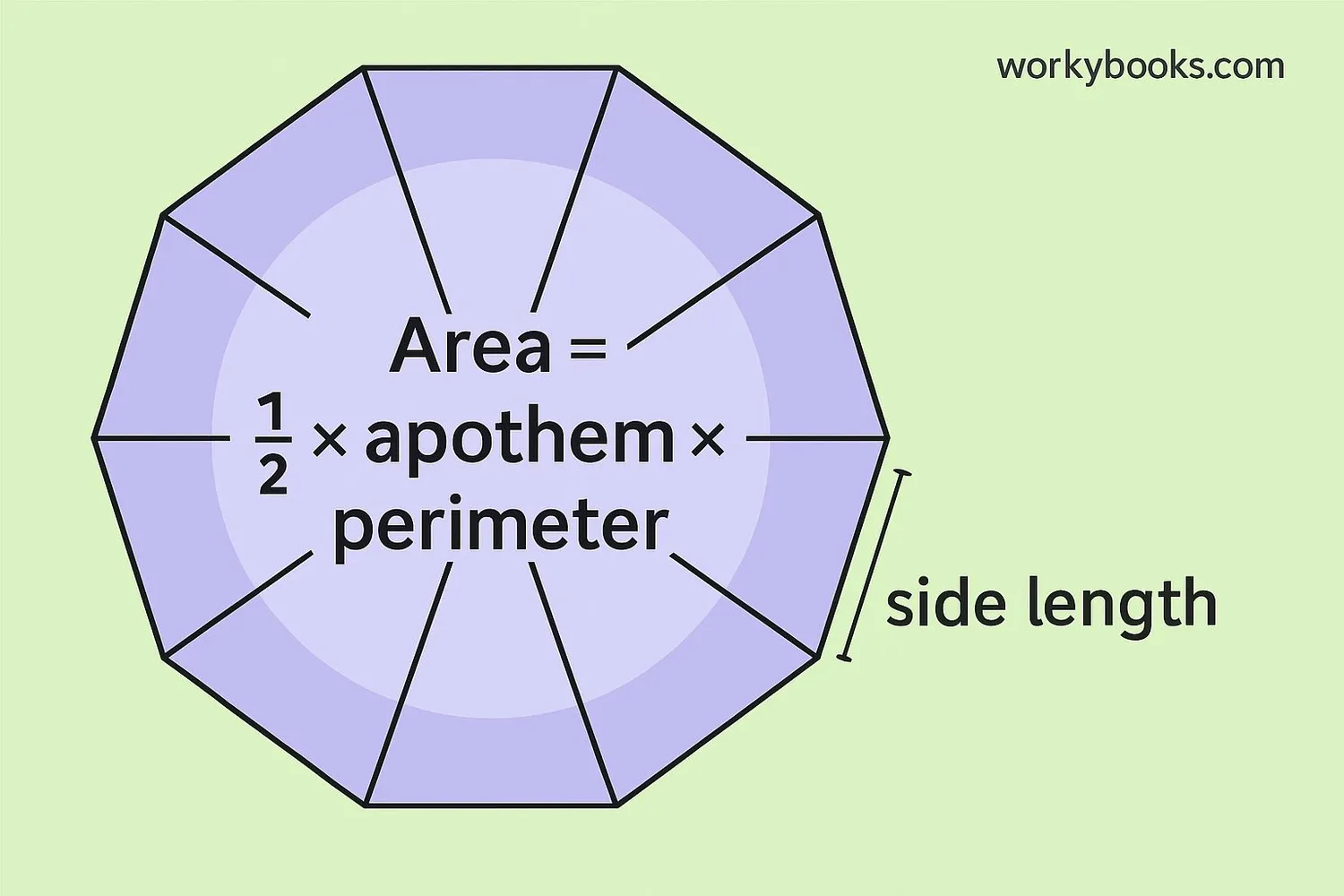
The area of a decagon is the amount of space inside the shape. Calculating area is a little more complex than perimeter, but we have a formula to help!
For a regular decagon (all sides equal, all angles equal):
Area Formula
Where s is the side length
Area Formula with Apothem
Example: A regular decagon has side length 8 cm and apothem 12.31 cm. What is its area?
Solution:
Step 1: Perimeter = 10 × 8 cm = 80 cm
Step 2: Area = (80 cm × 12.31 cm) ÷ 2 = 492.4 cm²
For irregular decagons, we can divide them into triangles and other shapes to calculate the total area.
Area Tip
For any regular polygon: Area = (Perimeter × Apothem) ÷ 2
Decagon Practice Quiz
Test your knowledge about decagons with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about decagons:
Shape Trivia
Discover interesting facts about polygons and decagons:
Ancient Geometry
The ancient Greeks studied decagons over 2000 years ago! Euclid, the famous mathematician, included properties of decagons in his book "Elements" around 300 BCE.
Nature's Patterns
While decagons are rare in nature, some flowers display pentagonal symmetry that relates to decagons. Sunflowers often have spiral patterns that follow mathematical sequences related to polygons.
Architectural Marvels
The Treasury of Atreus in Greece, built around 1250 BCE, features a decagonal layout. Many modern buildings use decagonal designs for their aesthetic appeal and structural strength.
Golden Ratio Connection
Regular decagons have a special relationship with the golden ratio (approximately 1.618). The ratio of a decagon's side length to its radius is 1/φ (1 divided by the golden ratio).





