Decagonal Prism - Definition, Examples, Quiz, FAQ, Trivia
Learn about this unique 3D shape with easy explanations, examples, and interactive activities
What is a Decagonal Prism?
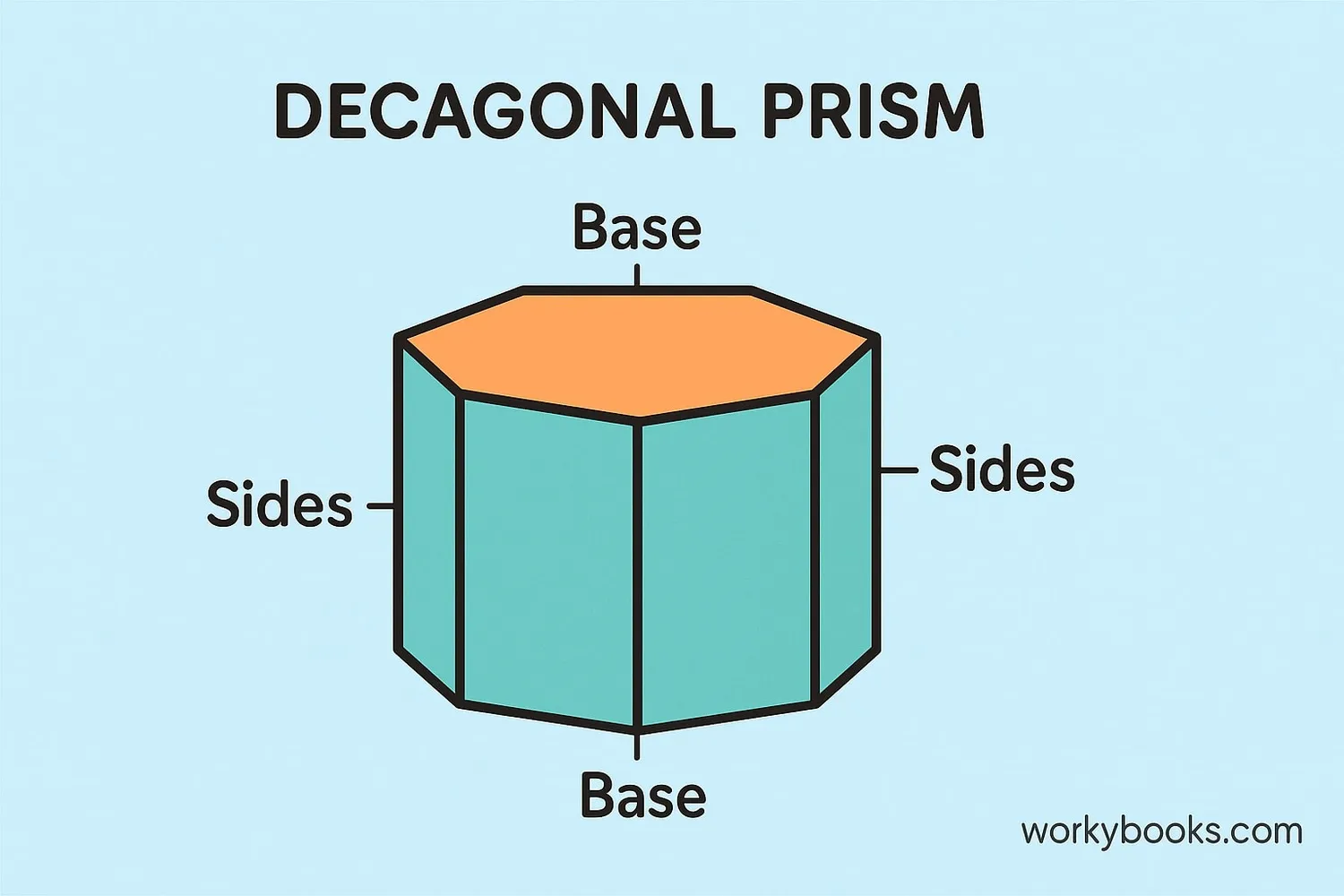
A decagonal prism is a three-dimensional shape with two parallel decagonal bases and ten rectangular sides connecting them.
Think of it like a building with a 10-sided floor and a matching 10-sided ceiling, connected by straight walls.
The word "decagonal" comes from "deca" meaning ten and "gon" meaning sides. So decagonal means 10-sided.
Decagonal prisms are all around us! Some buildings, towers, and even certain types of containers have this shape.
Key Concept
A decagonal prism has 2 decagonal bases (10-sided polygons) and 10 rectangular sides.
Properties of a Decagonal Prism
Decagonal prisms have special characteristics that make them unique. Here are their main properties:
Faces
A decagonal prism has 12 faces in total - 2 decagonal bases and 10 rectangular sides.
Vertices
It has 20 vertices (corner points). Each decagon has 10 vertices, and since they're connected, the total is 20.
Edges
There are 30 edges - 10 edges on each base (20 total) plus 10 edges connecting the bases.
Angles
The rectangular sides form 90° angles with each other. The decagonal bases have 144° interior angles.
Remember
Faces + Vertices = Edges + 2 (Euler's formula: F + V = E + 2)
Volume of a Decagonal Prism
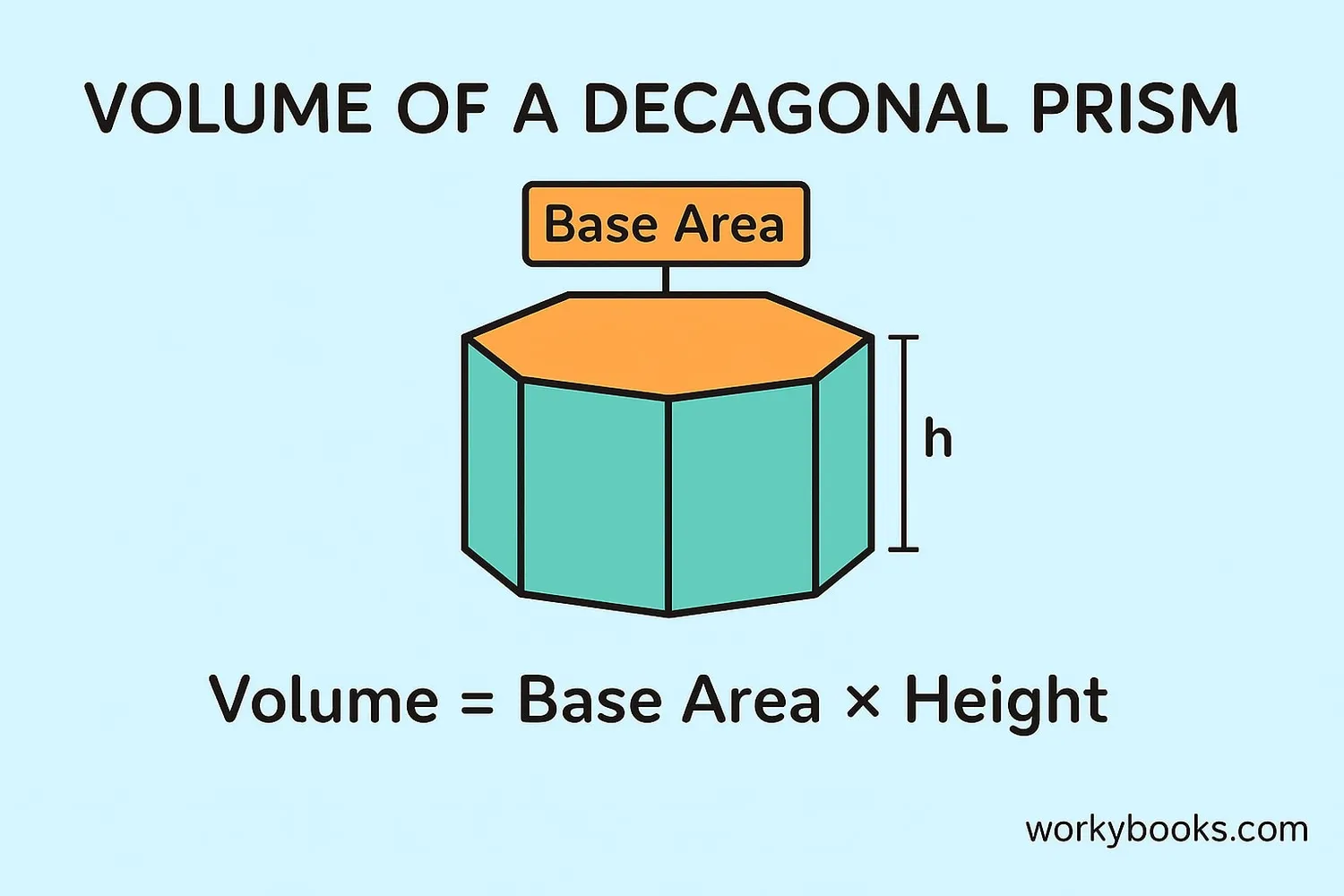
The volume of a decagonal prism tells us how much space it takes up. We calculate it using this formula:
Volume Formula
Where:
V = Volume
A = Area of the decagonal base
h = Height of the prism
For a regular decagon: A = (5/2) × s × a
Example: A decagonal prism has a base with side length 4 cm and apothem 6.16 cm. Its height is 10 cm.
Step 1: Calculate base area: (5/2) × 4 cm × 6.16 cm = 61.6 cm²
Step 2: Multiply by height: 61.6 cm² × 10 cm = 616 cm³
So the volume of this prism is 616 cubic centimeters.
Surface Area of a Decagonal Prism
Surface area is the total area of all the faces of a prism. For a decagonal prism:
Surface Area Formula
Where:
SA = Surface Area
A = Area of one decagonal base
P = Perimeter of the base
h = Height of the prism
Step 1: Calculate base areas: 2 × 61.6 cm² = 123.2 cm²
Step 2: Calculate lateral surface area: 40 cm × 10 cm = 400 cm²
Step 3: Add them together: 123.2 cm² + 400 cm² = 523.2 cm²
So the surface area of this prism is 523.2 square centimeters.
Real-World Examples

Decagonal prisms might seem special, but they appear in many places around us:
Architecture: Some towers and buildings have decagonal shapes to make them strong and visually interesting.
Containers: Certain types of containers, like pencil holders or decorative boxes, are made in this shape.
Nature: Some crystals and mineral formations naturally form decagonal prism shapes.
Everyday Objects: Look for decagonal prisms in toys, game pieces, or even some types of lamps.
Try This
Look around your home or classroom. Can you spot any objects that might be decagonal prisms?
Decagonal Prism Quiz
Test your knowledge about decagonal prisms with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about decagonal prisms:
Geometry Trivia
Discover interesting facts about prisms and geometry:
Ancient Geometry
The study of prisms dates back to ancient Egypt and Greece. The Greek mathematician Euclid wrote about prisms in his famous work "Elements" around 300 BCE.
Prisms in Nature
Some crystals naturally form prism shapes. Beryl crystals can form hexagonal prisms, and tourmaline often forms in triangular or nine-sided prisms.
Architectural Marvel
The Tower of Winds in Athens, Greece, is an octagonal prism structure built in the 1st century BCE. It functioned as a water clock and weather vane.
Light Prisms
While not decagonal, triangular prisms are used in science to split white light into a spectrum of colors. This is called dispersion.





