Decimal Representation of Rational Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn how fractions become decimals with easy explanations, examples, and practice activities
What Are Rational Numbers?

Rational numbers are numbers that can be written as a fraction where both the numerator (top number) and denominator (bottom number) are integers, and the denominator is not zero.
For example:
3 is rational because it can be written as 3/1
0.75 is rational because it equals 3/4
0.333... is rational because it equals 1/3
Key Concept
Rational numbers = fractions = terminating or repeating decimals
Terminating Decimals

A terminating decimal is a decimal that ends after a certain number of digits. It doesn't go on forever!
Examples of terminating decimals:
1/4 = 0.25
3/5 = 0.6
7/8 = 0.875
Why? The denominator 8 has prime factors of 2×2×2 (only 2s)
Remember
Terminating decimals have a limited number of digits after the decimal point.
Repeating Decimals
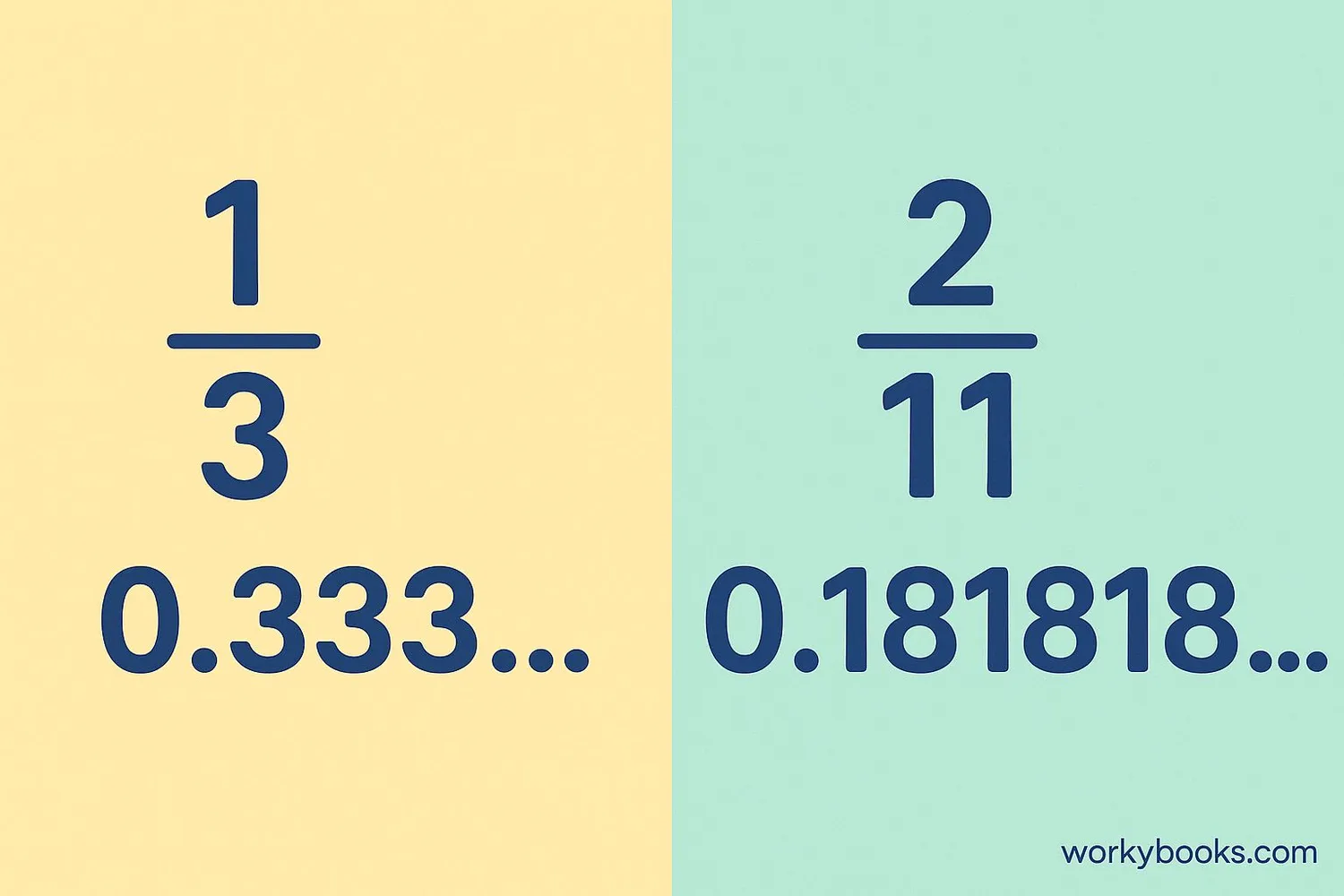
A repeating decimal has digits that go on forever in a repeating pattern. We show this with a bar over the repeating part.
Examples of repeating decimals:
2/9 = 0.2
5/6 = 0.83
1/7 = 0.142857
Why? The denominator 3 has a prime factor (3) that is not 2 or 5
Pattern Tip
Repeating decimals have a recurring pattern. Look for groups of digits that repeat.
Converting Rational Numbers to Decimals

Converting a rational number to a decimal is simple: just divide the numerator by the denominator!
Conversion Method
Use long division to convert any fraction to its decimal form.
Example 1: Convert 3/4 to a decimal
Step 1: Divide 3 by 4 → 3 ÷ 4
Step 2: 4 goes into 3.0 seven times (0.75)
Result: 0.75 (terminating)
Example 2: Convert 5/6 to a decimal
Step 1: Divide 5 by 6 → 5 ÷ 6
Step 2: 6 goes into 5.0 eight times with remainder 2 (0.8333...)
Result: 0.8333... = 0.83 (repeating)
Conversion Guide
| Fraction | Decimal | Type |
|---|---|---|
| 1/2 | 0.5 | Terminating |
| 1/3 | 0.333... | Repeating |
| 1/4 | 0.25 | Terminating |
| 1/5 | 0.2 | Terminating |
| 1/6 | 0.1666... | Repeating |
| 1/7 | 0.142857... | Repeating |
| 1/8 | 0.125 | Terminating |
| 1/9 | 0.111... | Repeating |
| 1/10 | 0.1 | Terminating |
Conversion Tip
To identify repeating decimals during division, look for repeating remainders.
Decimal Representation Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about rational numbers and decimals:
Math Trivia
Discover interesting facts about numbers and decimals:
Ancient Decimals
The concept of decimals dates back to ancient civilizations. The Chinese were using decimal fractions as early as the 4th century BC, while the Hindu-Arabic numeral system developed the decimal point in the 10th century.
Magic of 142857
The fraction 1/7 = 0.142857142857... This number is special because when multiplied by 2, 3, 4, 5, or 6, it produces cyclic permutations of the same digits: 142857 × 2 = 285714, ×3 = 428571, and so on!
Pi is Irrational
Unlike rational numbers, pi (π) is irrational. Its decimal representation never terminates and never repeats. We've calculated over 62 trillion digits of pi, and still no repeating pattern has been found!
Longest Repeating Pattern
The fraction with the longest repeating decimal for its denominator size is 1/97. It has a repeating sequence of 96 digits! This means the decimal repeats every 96 digits: 0.01030927... and so on for 96 digits before repeating.





