Decimal to Hexadecimal (Base 10 to Base 16) - Definition, Examples, Quiz, FAQ, Trivia
Learn to convert between decimal and hexadecimal number systems with easy explanations and practice activities
What is Hexadecimal?

Decimal is our everyday number system that uses 10 digits (0-9). This is called base-10 because it has 10 possible digits.
Hexadecimal is a number system that uses 16 digits: 0-9 and then A-F (where A=10, B=11, C=12, D=13, E=14, F=15). This is called base-16 because it has 16 possible digits.
Why do we need hexadecimal? Computers use binary (base-2) which is very long to write. Hexadecimal is a shorter way to represent binary numbers. Each hexadecimal digit represents 4 binary digits (bits).
Key Concept
Hexadecimal is base-16 and uses digits 0-9 and letters A-F to represent values 10-15.
How to Convert Decimal to Hexadecimal
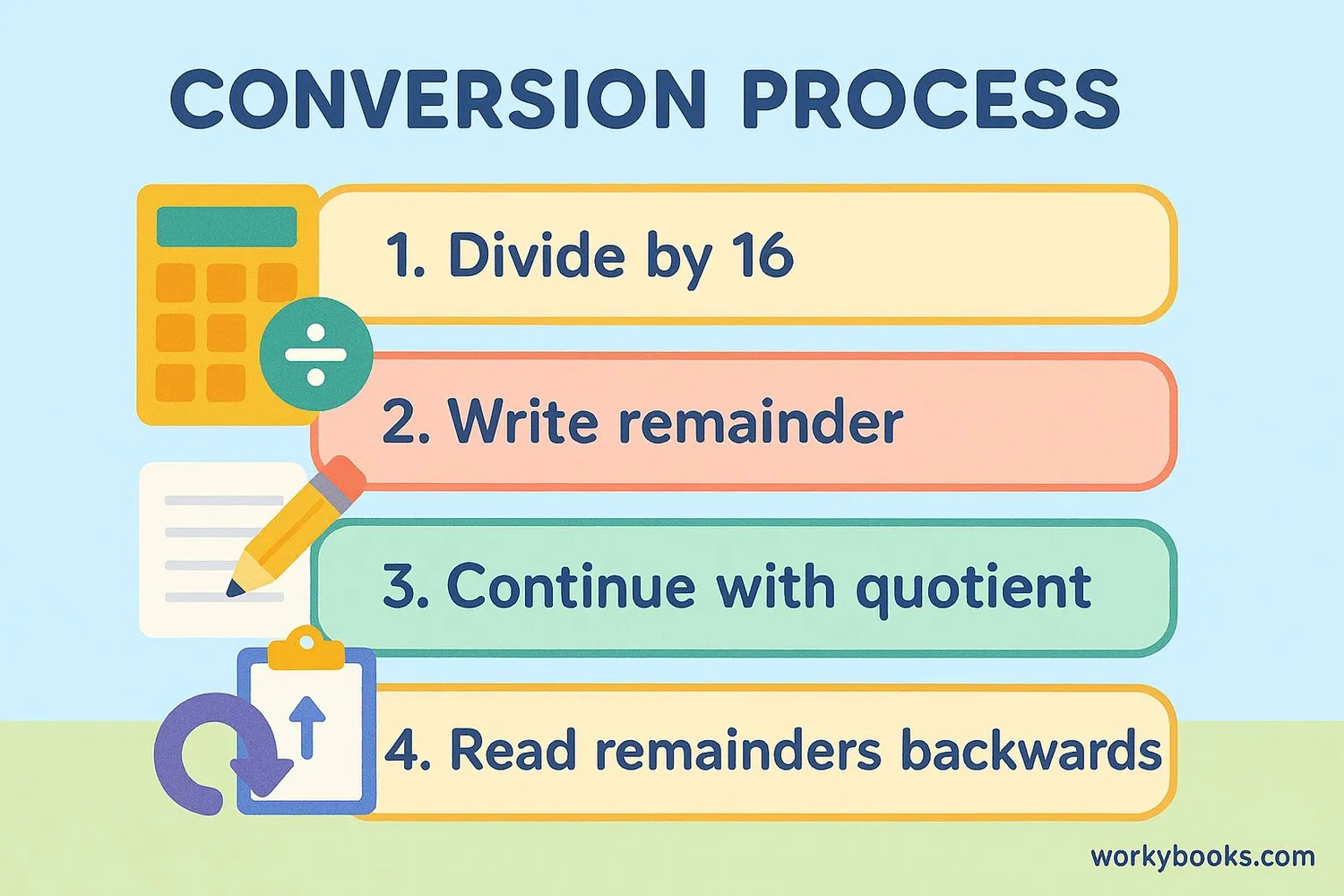
Converting decimal to hexadecimal is easy once you learn the steps:
Conversion Steps
- Divide the decimal number by 16
- Write down the remainder (convert to hex digit if needed)
- Divide the quotient by 16 again
- Repeat until quotient is zero
- Read the remainders from last to first
Example: Convert 25510 to hexadecimal
Step 1: 255 ÷ 16 = 15 remainder 15 → F
Step 2: 15 ÷ 16 = 0 remainder 15 → F
Step 3: Read remainders backwards: FF
So 25510 = FF16
Remember
Always convert remainders 10-15 to hexadecimal digits: A=10, B=11, C=12, D=13, E=14, F=15
Decimal to Hexadecimal Converter
Use this tool to convert any decimal number to hexadecimal. Enter a number between 0 and 10000 and click "Convert to Hex" to see the result!
Practice Tip
Try converting these numbers: 10, 16, 32, 100, 255. Notice any patterns?
Conversion Examples
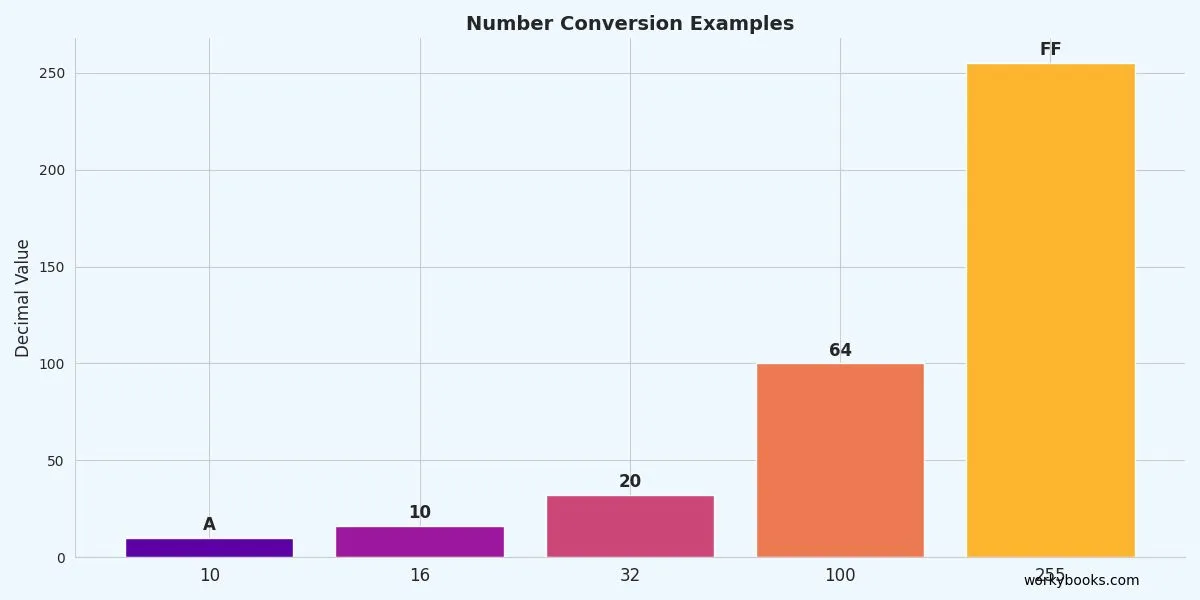
Let's practice with more examples:
Example 1: Convert 1010 to hexadecimal
10 ÷ 16 = 0 remainder 10 → A
Result: 1010 = A16
Example 2: Convert 1610 to hexadecimal
16 ÷ 16 = 1 remainder 0 → 0
1 ÷ 16 = 0 remainder 1 → 1
Result: 1610 = 1016
Example 3: Convert 10010 to hexadecimal
100 ÷ 16 = 6 remainder 4 → 4
6 ÷ 16 = 0 remainder 6 → 6
Result: 10010 = 6416
Example 4: Convert 50010 to hexadecimal
500 ÷ 16 = 31 remainder 4 → 4
31 ÷ 16 = 1 remainder 15 → F
1 ÷ 16 = 0 remainder 1 → 1
Result: 50010 = 1F416
Common Decimal to Hexadecimal Conversions
| Decimal | Hexadecimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | A |
| 15 | F |
| 16 | 10 |
| 32 | 20 |
| 64 | 40 |
| 100 | 64 |
| 255 | FF |
| 512 | 200 |
Conversion Tip
Notice that powers of 16 have special hexadecimal representations: 161 = 1016, 162 = 10016, etc.
Conversion Practice Quiz
Test your conversion skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about decimal to hexadecimal conversion:
Number System Trivia
Discover interesting facts about number systems:
Ancient Number Systems
The ancient Babylonians used a base-60 number system around 2000 BCE. This system is why we have 60 seconds in a minute and 60 minutes in an hour today!
Binary Origins
The binary number system was first described by Gottfried Leibniz in 1679, but it didn't become important until the development of computers in the 20th century.
Hexadecimal in Computers
Hexadecimal is commonly used to represent memory addresses, color codes (like #FF0000 for red), and error codes in computer systems.
Base-12 Systems
Some cultures used base-12 systems, counting with their thumb to touch each finger bone (3 per finger × 4 fingers = 12). This is why we have 12 months in a year and 12 inches in a foot.


