Understanding Decimals - Definition, Examples, Quiz, FAQ, Trivia
Learn about decimal numbers with easy explanations, visual examples, and practice activities
What are Decimals?

Decimals are numbers that have a whole number part and a fractional part separated by a decimal point. They help us represent numbers that are not whole.
For example, 2.5 means 2 whole parts and 0.5 (or half) of another part. Decimals are based on the number 10, which makes them easy to work with.
Think of decimals as a way to write fractions with denominators of 10, 100, 1000, etc. For instance:
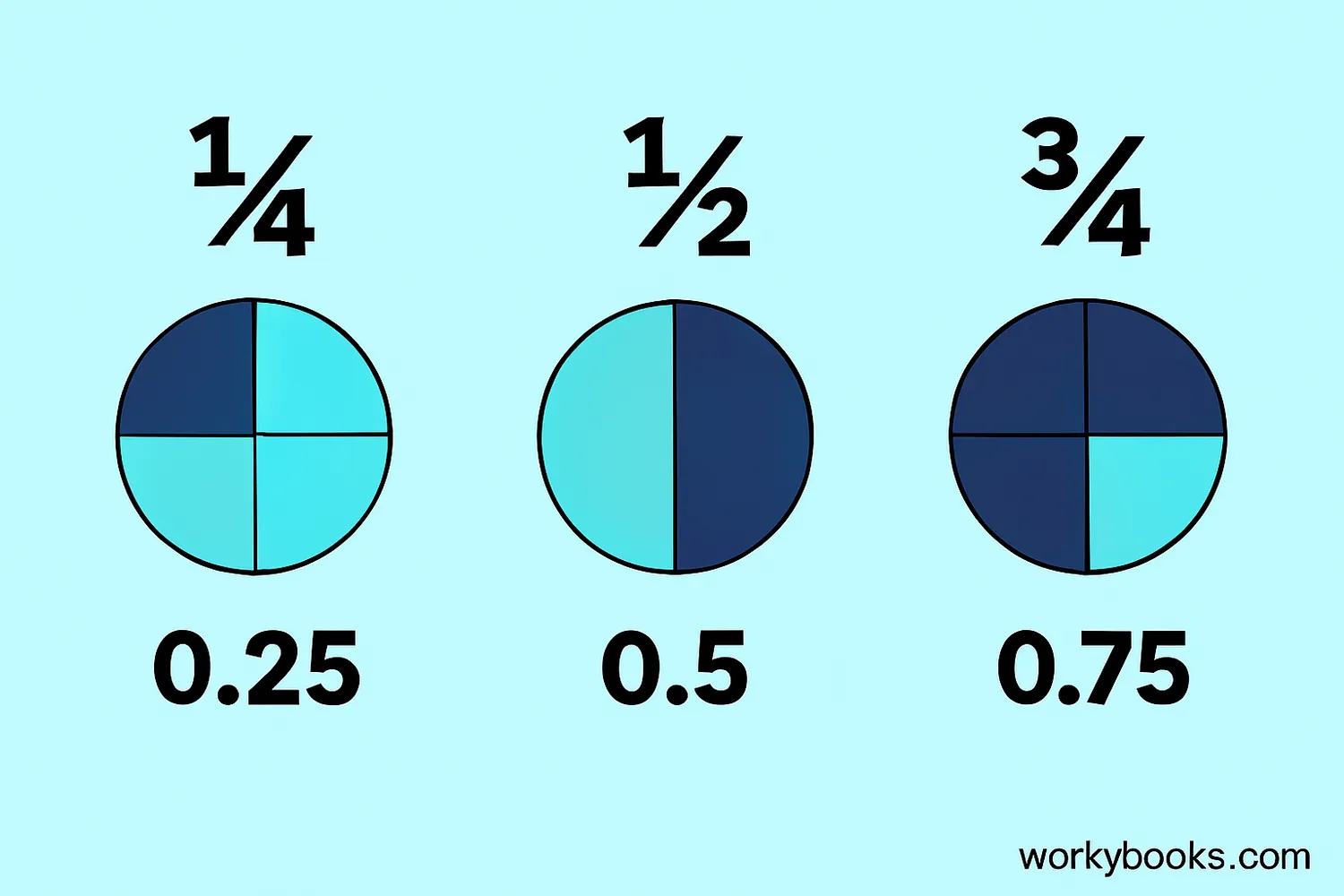
- 0.1 = 1/10 (one-tenth)
- 0.25 = 25/100 = 1/4 (one-quarter)
- 0.75 = 75/100 = 3/4 (three-quarters)
Key Concept
Decimals extend our number system to values between whole numbers. The decimal point separates the whole number part from the fractional part.
The Decimal Point
The decimal point (.) is the most important part of a decimal number. It separates the whole number part on the left from the fractional part on the right.
For example, in the number 15.75:
- 15 is the whole number part
- 75 is the fractional part
The decimal point tells us where the whole number ends and the fraction begins. Without it, we wouldn't know if 1575 meant one thousand five hundred seventy-five or fifteen and seventy-five hundredths!
Remember
In some countries, a comma is used instead of a point (like 15,75), but in mathematics, we use the decimal point (15.75).
Place Value of Decimals
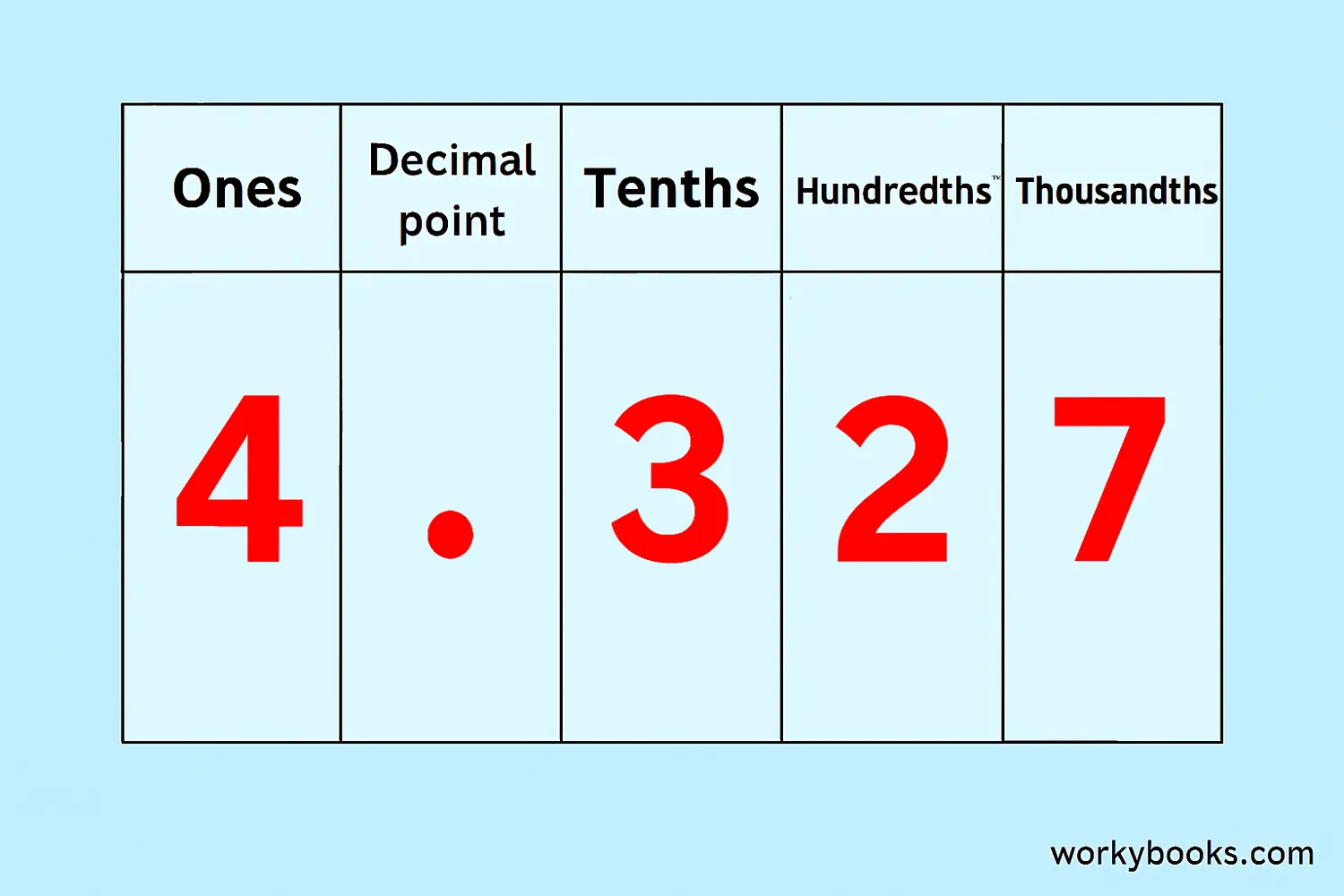
Just like whole numbers have place values (ones, tens, hundreds), decimals have place values too! The places to the right of the decimal point are called tenths, hundredths, thousandths, and so on.
Let's look at the number 23.456:
So 23.456 means:
2 tens + 3 ones + 4 tenths + 5 hundredths + 6 thousandths
or 20 + 3 + 0.4 + 0.05 + 0.006
Place Value Tip
Each place to the right is 10 times smaller than the place to its left. For example, 1 tenth = 10 hundredths.
Converting Fractions to Decimals
Fractions and decimals are two ways to represent the same value. We can convert fractions to decimals by dividing the numerator (top number) by the denominator (bottom number).
Conversion Formula
To convert a fraction to a decimal, divide the top number by the bottom number.
Example 1: Convert 3/4 to a decimal
Step 1: Divide 3 by 4 → 3 ÷ 4
Step 2: Calculate the result → 0.75
Example 2: Convert 2/5 to a decimal
Step 1: Divide 2 by 5 → 2 ÷ 5
Step 2: Calculate the result → 0.4
Some fractions convert to decimals that end (like 1/4 = 0.25), while others repeat (like 1/3 = 0.333...).
Conversion Tip
For fractions with denominators that are factors of 10 (like 2, 4, 5), you can convert to tenths, hundredths, or thousandths.
Types of Decimals

Decimals come in different types based on how they end (or don't end!):
1. Terminating Decimals: These decimals end after a certain number of digits.
Examples: 0.5, 0.25, 3.75
2. Repeating Decimals: These decimals have one or more digits that repeat forever.
Examples: 0.333... (written as 0.\overline{3}), 0.1666... (written as 0.1\overline{6})
3. Non-Terminating, Non-Repeating Decimals: These decimals go on forever without repeating. Most famous example is π (pi) ≈ 3.1415926535...
Understanding these types helps us work with different kinds of numbers and know when we can write them as fractions.
Did You Know?
Terminating decimals can always be written as fractions with denominators that are powers of 10 (like 10, 100, 1000).
Decimal Practice Quiz
Test your decimal knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about decimals:
Decimal Trivia
Discover interesting facts about decimals and numbers:
Decimal History
The decimal system was developed by Persian mathematician Al-Kashi in the 15th century. He used decimals to calculate π to 16 decimal places - an amazing achievement for his time!
Decimal Currency
The US didn't always use decimal currency! Before 1792, various coins from different countries circulated. The Coinage Act of 1792 established the US dollar with cents (1/100 dollar), creating our decimal money system.
Calculator Precision
Most calculators can display up to 8-10 decimal places, but computer systems can calculate with hundreds of decimal places. The world record for calculating π is over 100 trillion decimal places!
Metric System
The metric system is entirely based on decimals. All units relate by powers of 10: 1 meter = 100 centimeters, 1 kilometer = 1000 meters. This makes conversions much easier than imperial measurements.





