Decomposing Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn how to break fractions into smaller parts with step-by-step explanations and practice activities
What is Decomposing Fractions?
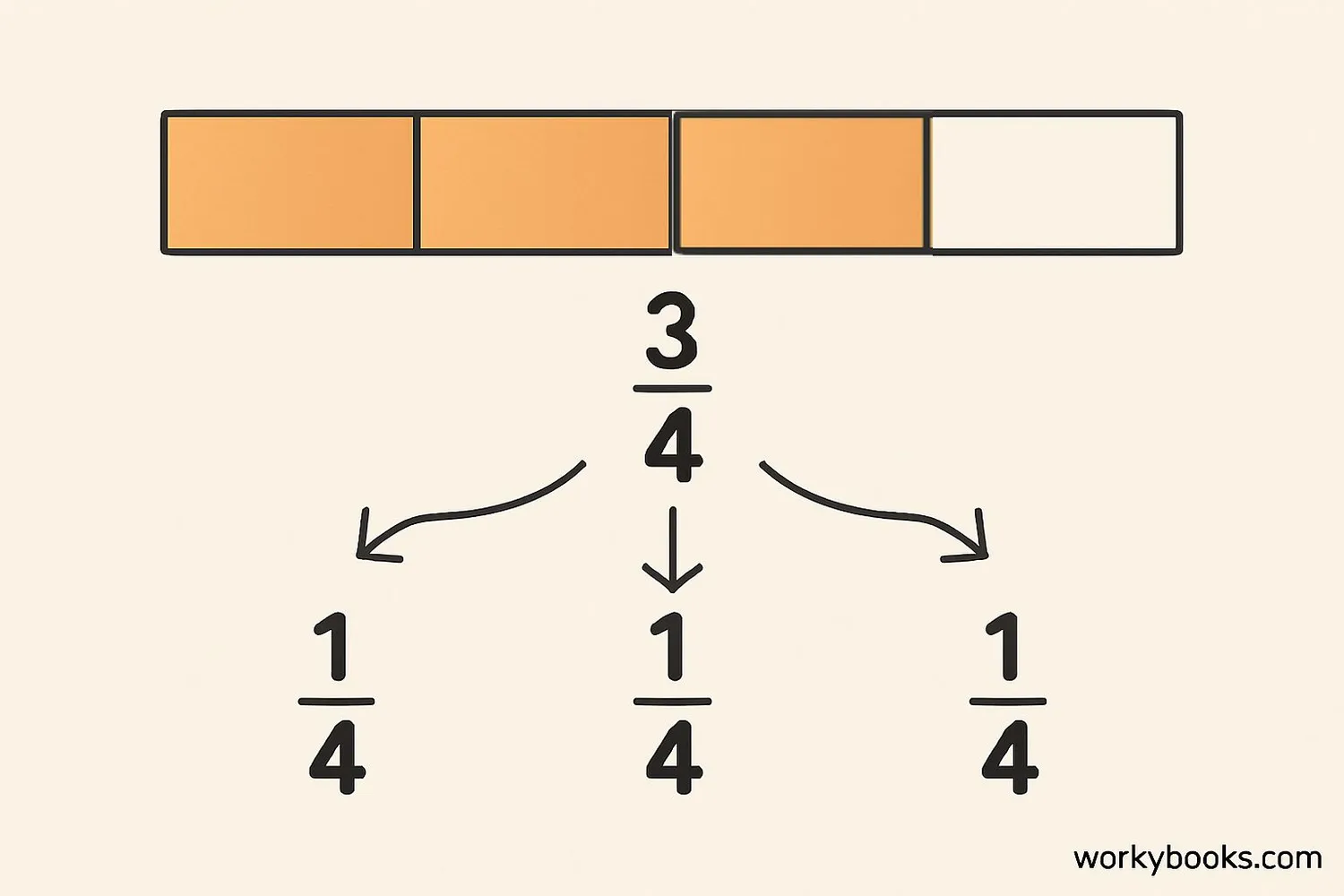
Decomposing fractions means breaking a fraction down into smaller fractions that add up to the original fraction. It's like taking a whole pizza and dividing it into smaller slices that together make the whole pizza.
For example, the fraction 58 can be decomposed as:
58 =
18 +
28 +
28
Decomposing helps us understand fractions better and makes it easier to add, subtract, or compare them. It's an important skill in mathematics that builds a strong foundation for more advanced concepts.
Key Concept
Decomposing fractions helps us see that fractions are made up of smaller parts, especially unit fractions (fractions with 1 as the numerator).
How to Decompose Fractions

Decomposing fractions is simple when you follow these steps:
Step 1: Identify the denominator (bottom number) of your fraction. This tells you how many equal parts the whole is divided into.
Step 2: Think of different ways to add fractions with the same denominator to get your original fraction.
Step 3: Write your decomposition as an addition equation.
Let's practice with an example:
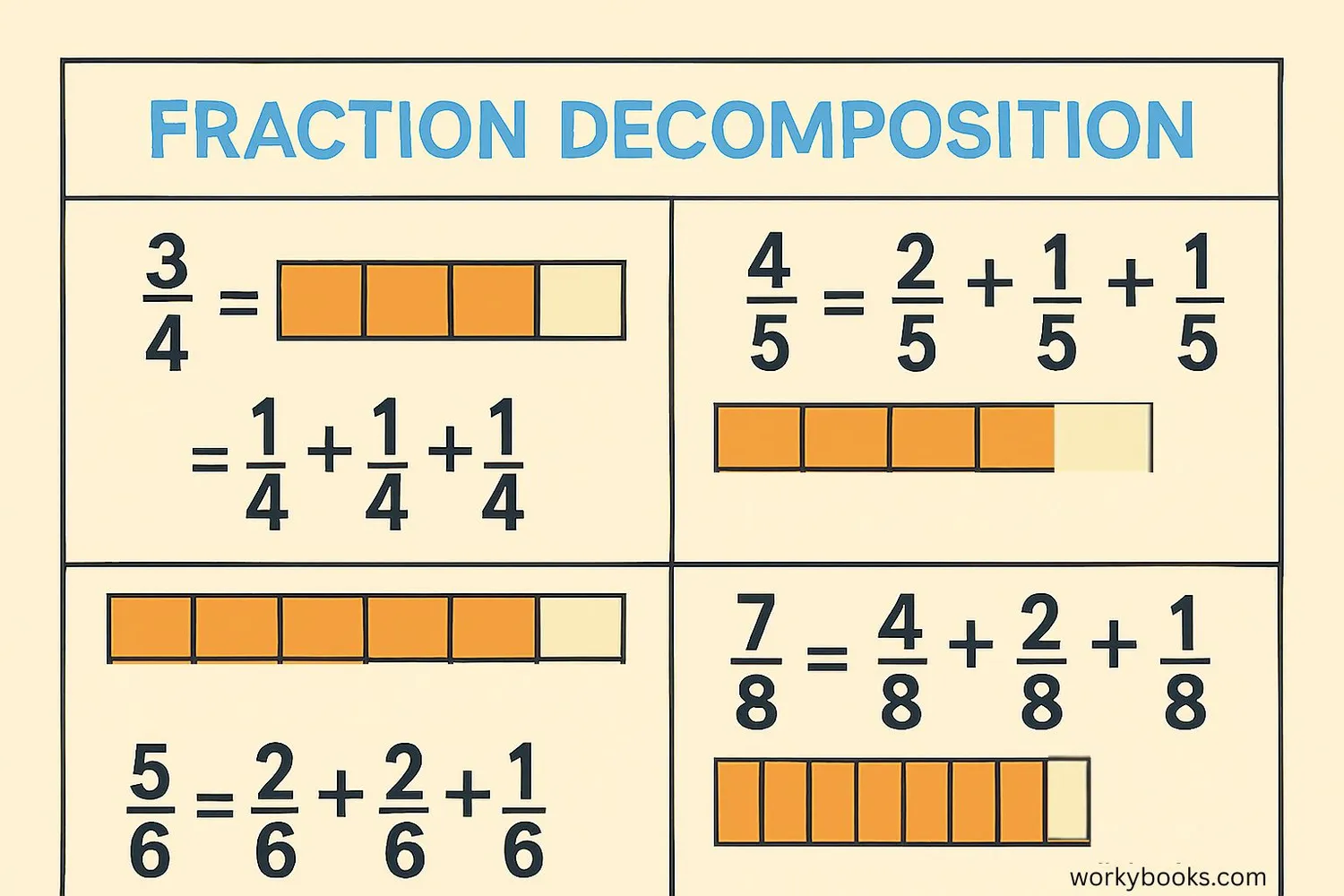
Example: Decompose 34
Solution 1: 34 =
14 +
14 +
14
Solution 2: 34 =
24 +
14
Solution 3: 34 =
12 +
14
All these are correct decompositions!
Remember
There are often multiple ways to decompose a fraction. The important thing is that all the parts add up to the original fraction.
Decomposing Mixed Numbers
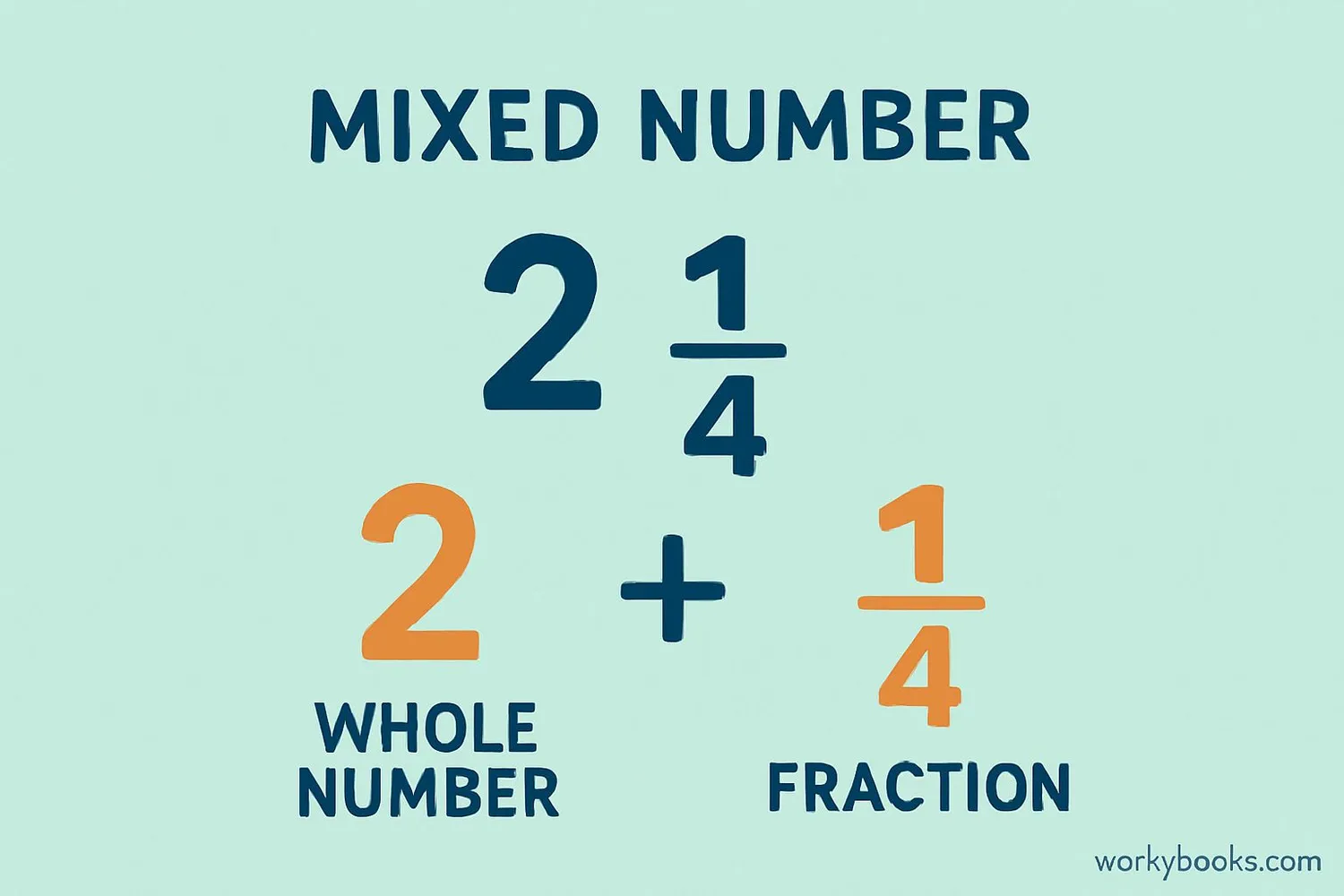
A mixed number is a whole number combined with a fraction (like 214).
Decomposing mixed numbers helps us understand them better and prepares us for operations like addition and subtraction.
Step 1: Separate the whole number part from the fraction part.
Step 2: Decompose the fraction part as you would with any fraction.
Step 3: Combine the whole number with the decomposed fractions.
Example: Decompose 235
Step 1: Separate into 2 + 35
Step 2: Decompose 35 =
15 +
25
Step 3: Combine: 2 + 15 +
25
Another way: 235 =
1 + 1 + 35 =
1 + 135
Tip
When decomposing mixed numbers, you can break the whole number into smaller whole numbers too!
Examples
Solution 1: 56 =
16 +
16 +
16 +
16 +
16
Solution 2: 56 =
36 +
26
Solution 1: 313 =
1 + 1 + 1 + 13
Solution 2: 313 =
2 + 113
Solution 3: 313 =
103 =
33 +
33 +
33 +
13
Solution: 78 = 18 + 18 + 18 + 18 + 18 + 18 + 18
Practice Tip
Try to find at least three different ways to decompose each fraction. This will help you understand fractions better!
Practice Quiz
Test your fraction decomposition skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about decomposing fractions:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they only used unit fractions (with numerator 1). They would write any fraction as a sum of unit fractions.
Fractions in Nature
Fractions appear everywhere in nature! Beehives have hexagonal cells that can be divided into fractional parts, and flower petals often grow in fractional patterns.
Fractions in Music
Musical rhythms are based on fractions! A whole note lasts 4 beats, a half note 2 beats, a quarter note 1 beat, and so on. Fractions help musicians keep time.
Fraction Records
The smallest fraction commonly used is 1/64, but mathematicians work with much smaller fractions. In computer science, fractions can be as small as 1/1,000,000,000!





