Diagonals - Definition, Examples, Quiz, FAQ, Trivia
Learn about diagonals in geometry with easy explanations, examples, and practice activities
What is a Diagonal?
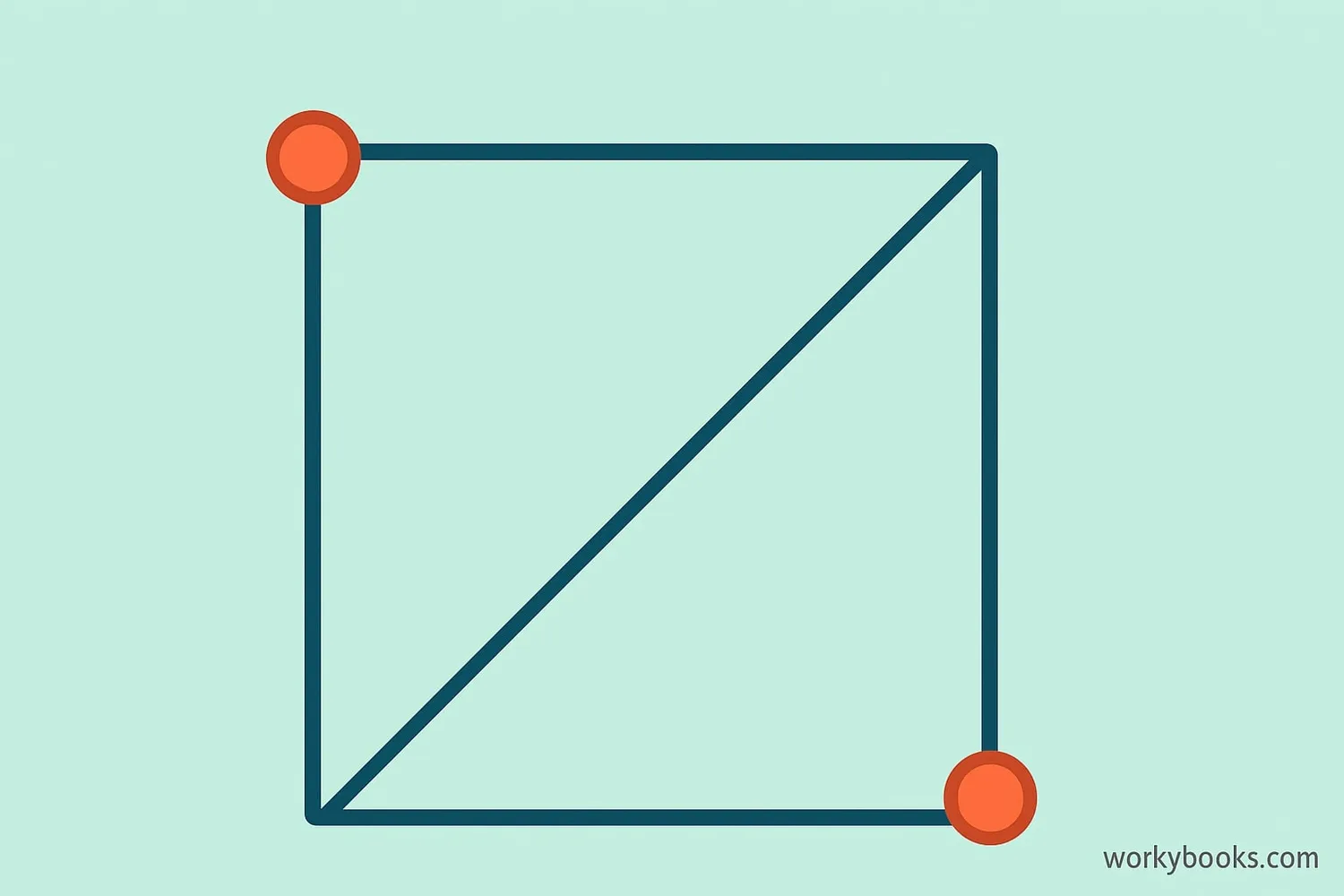
A diagonal is a straight line that connects two non-adjacent corners (vertices) in a polygon. In simpler terms, it's a line that goes across a shape from one corner to another corner that isn't right next to it.
Think of a square: if you draw a line from the top-left corner to the bottom-right corner, that's a diagonal! Diagonals are different from sides because they go through the inside of the shape.
Diagonals help us understand the properties of shapes. For example, in a rectangle, the diagonals are always equal in length. In a square, the diagonals are equal and they cross at the center, making right angles.
Key Concept
Diagonals connect non-adjacent vertices. They are always inside the shape for convex polygons.
Diagonals in Different Shapes
Diagonals behave differently in various shapes. Let's explore how diagonals work in common polygons:
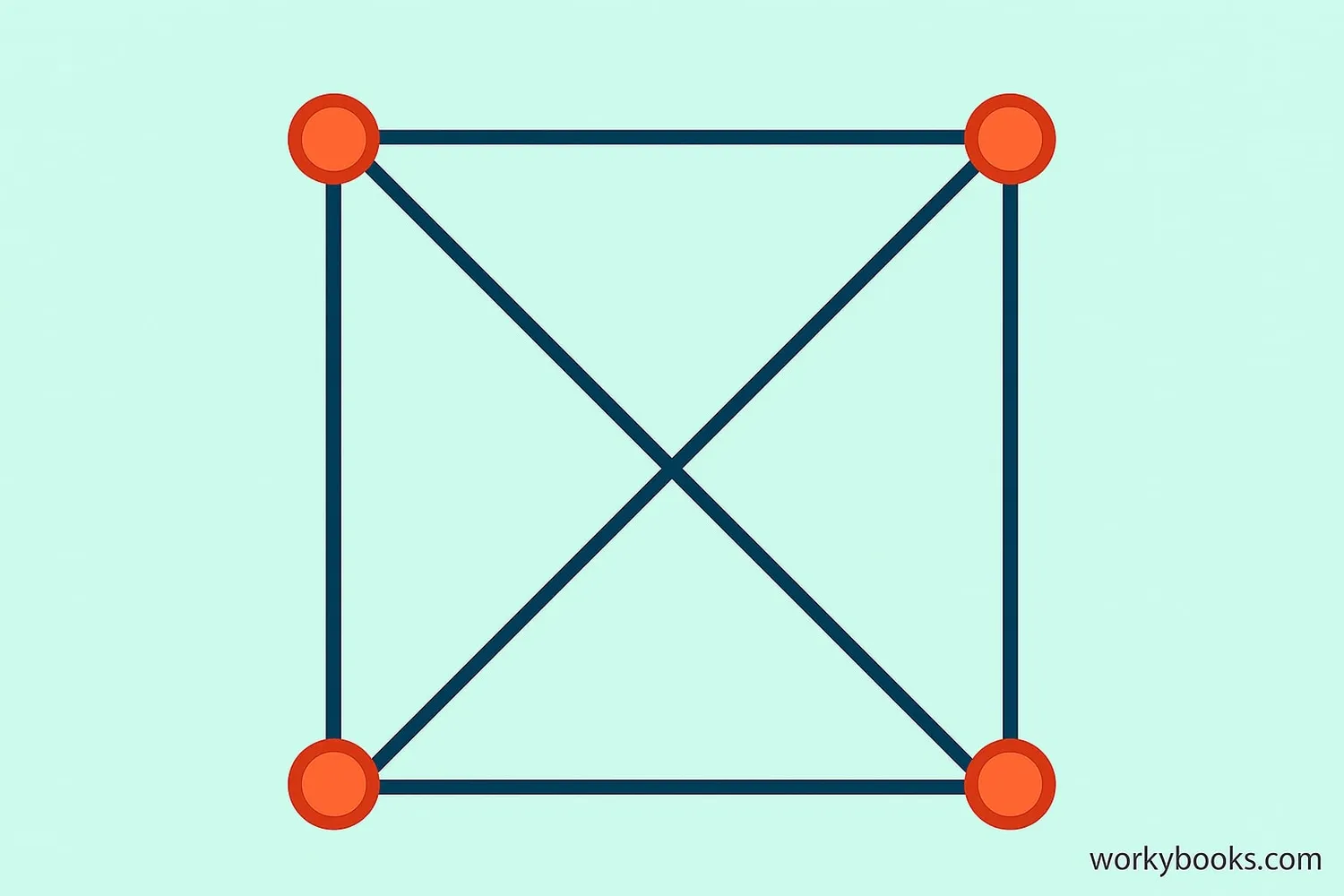
In a square, both diagonals are equal in length. They bisect each other at 90° angles and divide the square into two congruent right triangles.
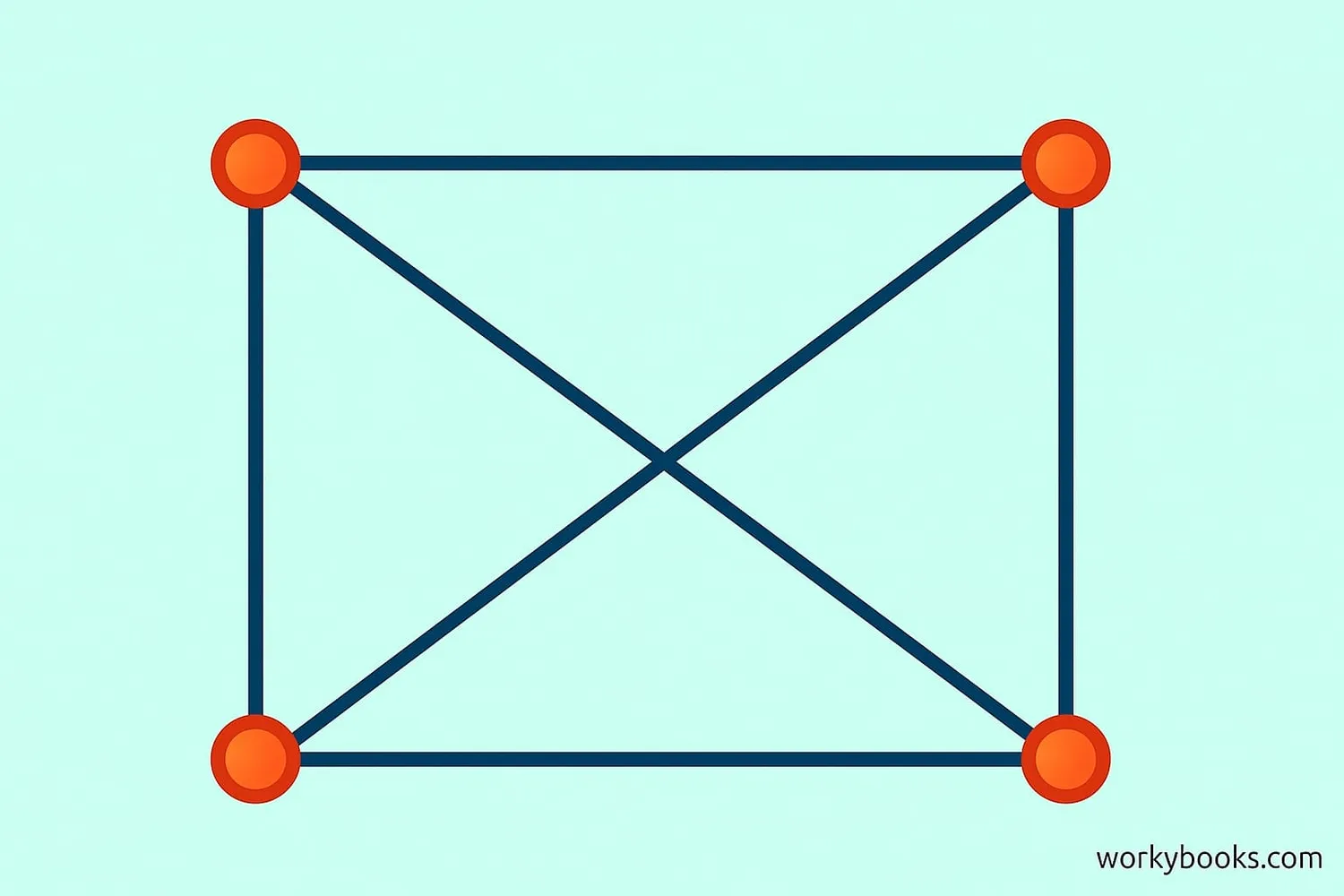
Rectangles have two diagonals of equal length that bisect each other. They divide the rectangle into two congruent right triangles.
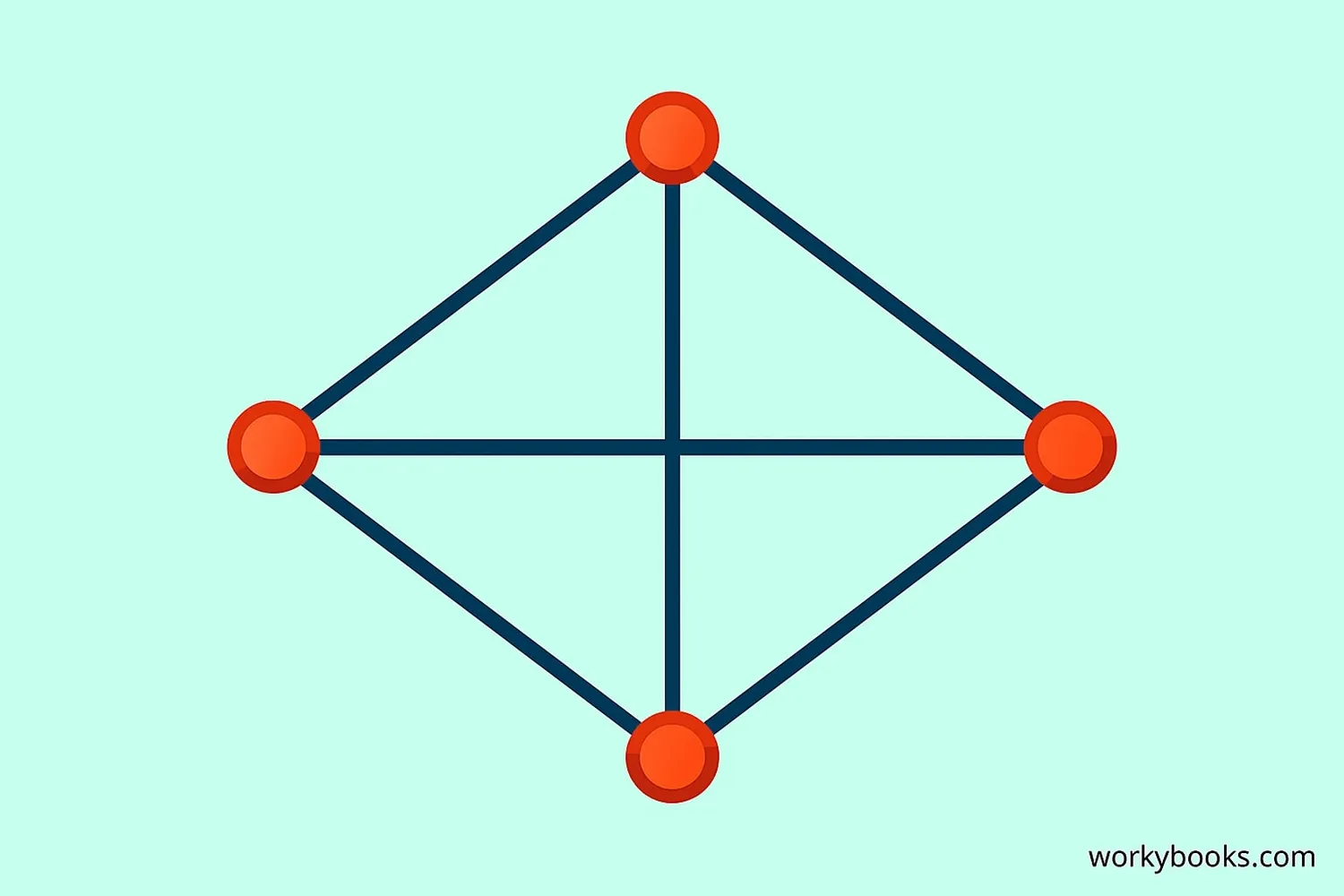
In a rhombus, the diagonals bisect each other at right angles (90°). They are of different lengths unless it's a square.
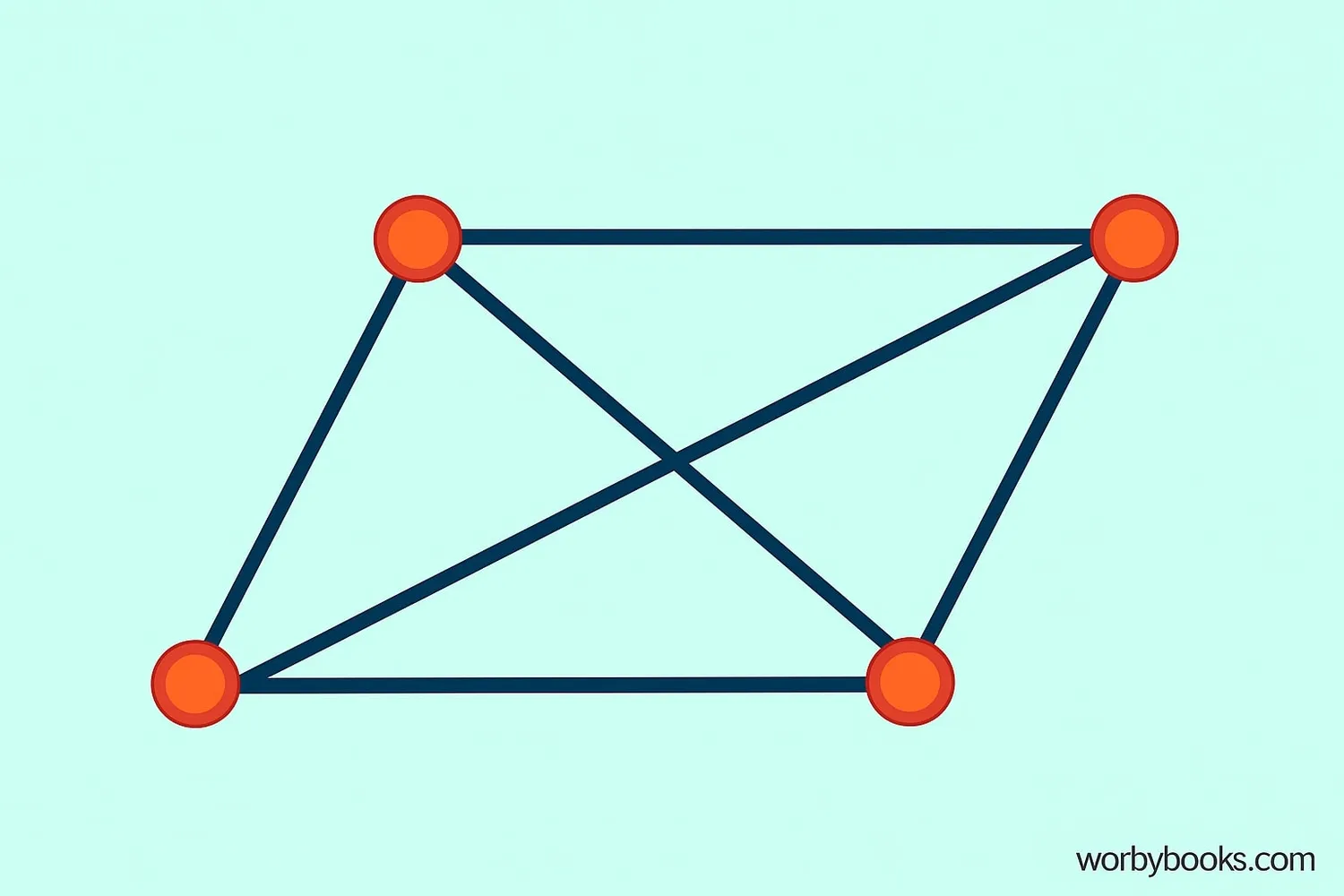
The diagonals of a parallelogram bisect each other but are not necessarily equal or perpendicular.
Remember
Triangles have no diagonals because all vertices are adjacent to each other!
Diagonal Formulas
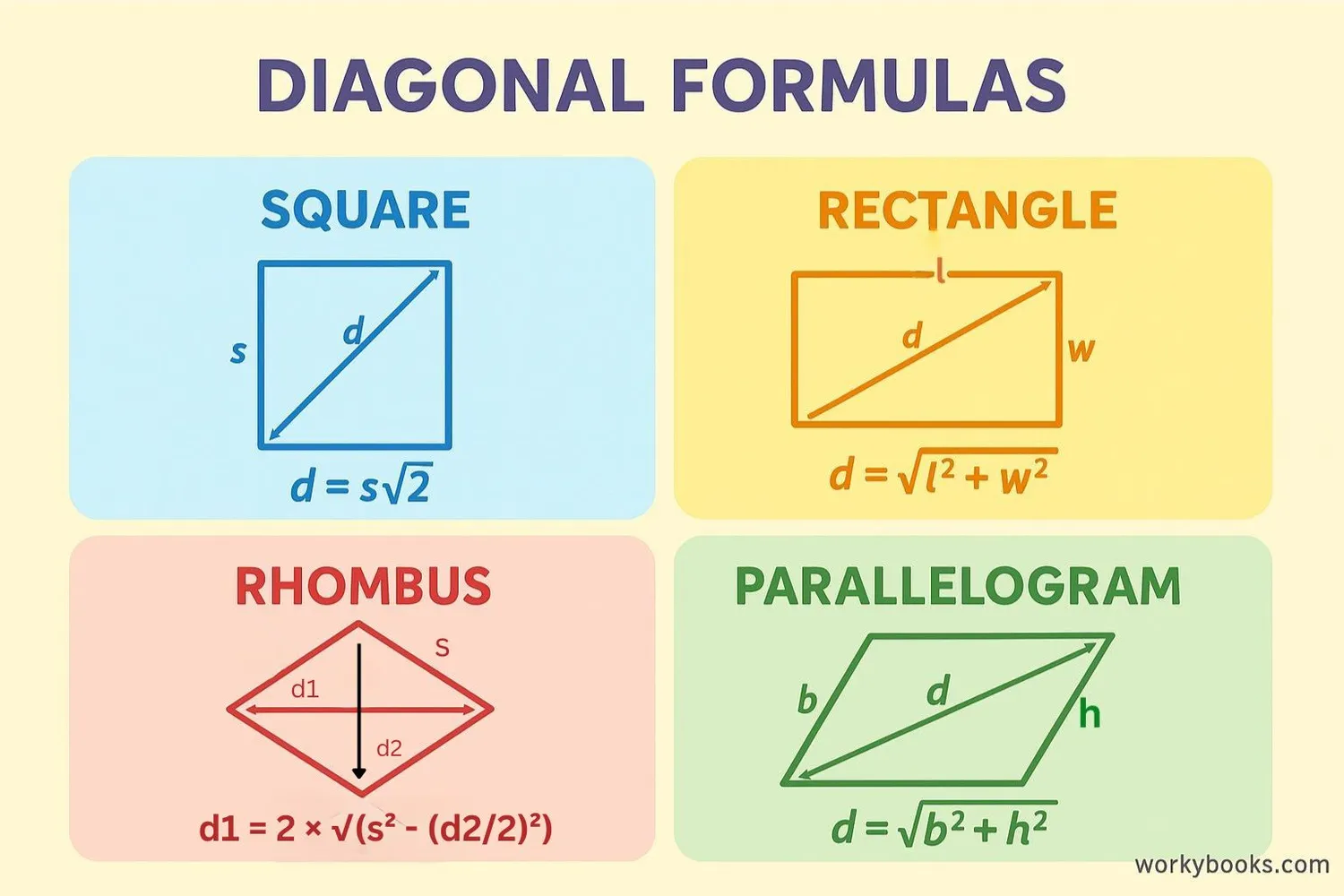
We can calculate the length of diagonals in different shapes using mathematical formulas:
Diagonal of a Square
Where 's' is the side length of the square. The diagonal is always longer than the sides!
Diagonal of a Rectangle
Where 'l' is the length and 'w' is the width of the rectangle. This is the Pythagorean theorem!
Diagonals of a Rhombus
Where 's' is the side length, and d1 and d2 are the two diagonals. The diagonals bisect each other at right angles.
Formula Tip
The rectangle diagonal formula is actually the Pythagorean theorem! The diagonal is the hypotenuse of a right triangle formed by the length and width.
Number of Diagonals in a Polygon
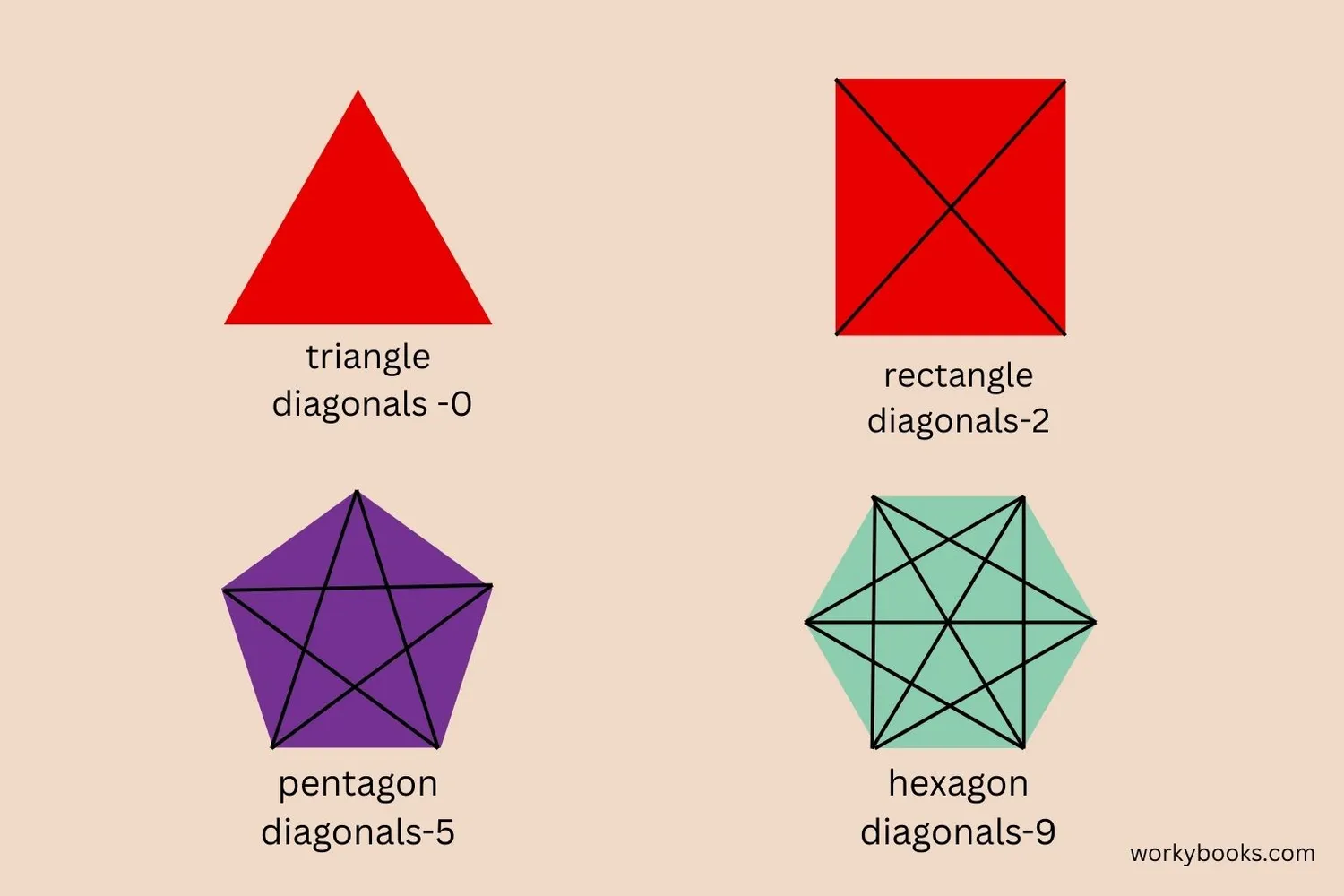
The number of diagonals in a polygon depends on how many sides it has. We can calculate it using this formula:
Diagonal Count Formula
Where 'n' is the number of sides in the polygon.
- The vertex itself
- The two adjacent vertices
Examples of Diagonal Counts
| Polygon | Sides (n) | Diagonals |
|---|---|---|
| Triangle | 3 | 0 |
| Quadrilateral | 4 | 2 |
| Pentagon | 5 | 5 |
| Hexagon | 6 | 9 |
| Heptagon | 7 | 14 |
| Octagon | 8 | 20 |
Diagonal Quiz
Test your knowledge about diagonals with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about diagonals:
Geometry Trivia
Discover interesting facts about diagonals and geometry:
Ancient Use of Diagonals
The ancient Egyptians used diagonals to create right angles for pyramid construction. They would make a rope with 12 equally spaced knots, stretch it to form a 3-4-5 triangle, creating a perfect right angle.
Diagonal in Nature
Many crystals form in diagonal patterns. Snowflakes often have diagonals in their intricate designs, and spider webs use diagonal strands to create strong, flexible structures.
Chess Diagonals
In chess, bishops move only diagonally across the board. A bishop on an empty chessboard can reach 13 squares diagonally from the center position.
Longest Diagonal
The longest possible diagonal in a regular polygon with straight sides is in a megagon (1,000,000 sides). Its diagonal would be almost equal to its diameter!




