Diagonal of a Square - Definition, Examples, Quiz, FAQ, Trivia
Learn about square diagonals with visual explanations, formulas, and practice activities
What is a Diagonal?
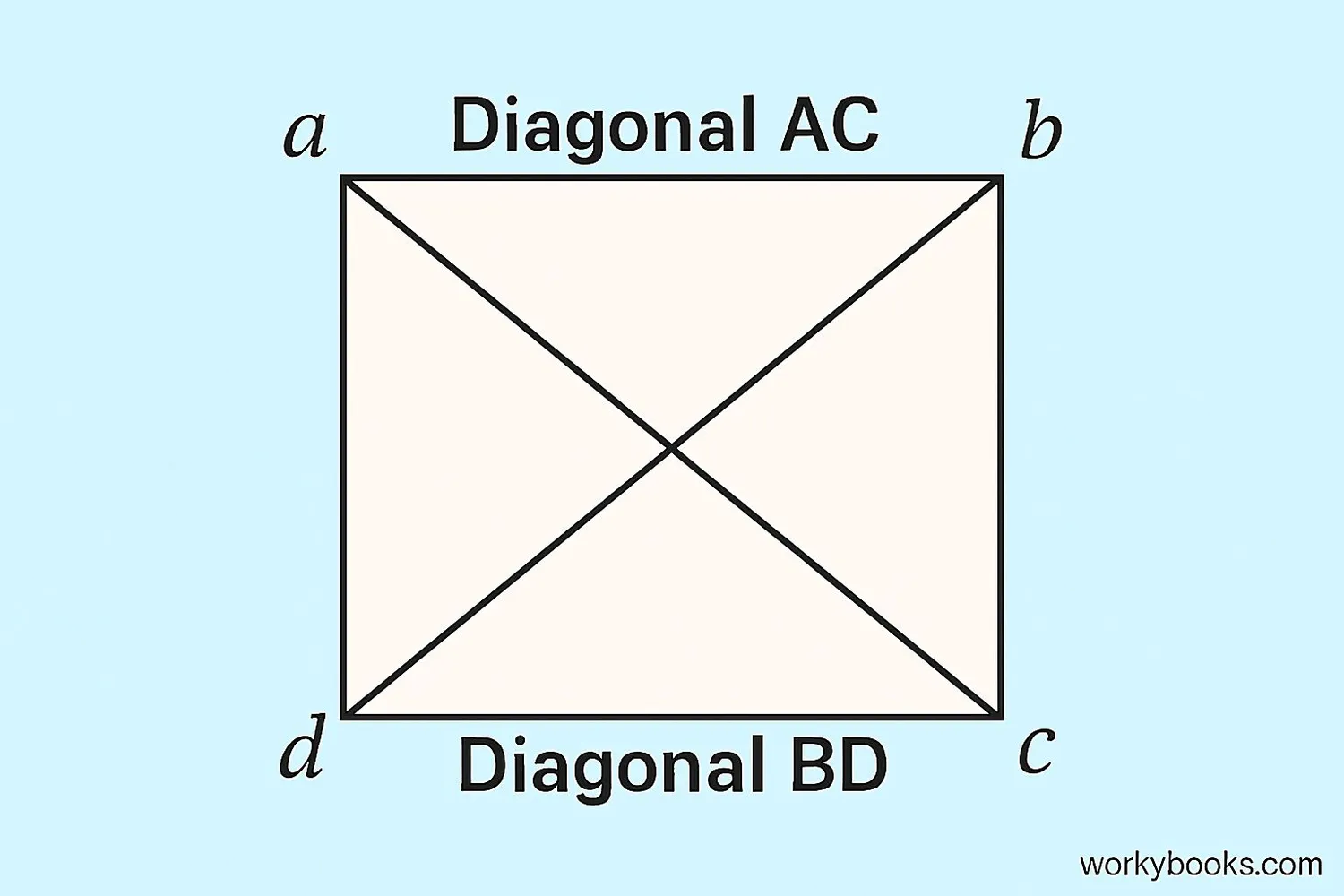
A diagonal is a straight line that connects two opposite corners of a square. Every square has two diagonals that are equal in length and cross at the center of the square.
Diagonals are important in geometry because they help us understand the properties of shapes. For squares, the diagonals have special relationships with the sides and angles.
Key characteristics:
- Diagonals connect opposite vertices (corners)
- Each square has two diagonals
- Diagonals are longer than the sides
Key Concept
The diagonal is the longest straight line you can draw inside a square, connecting two opposite corners.
Properties of Square Diagonals
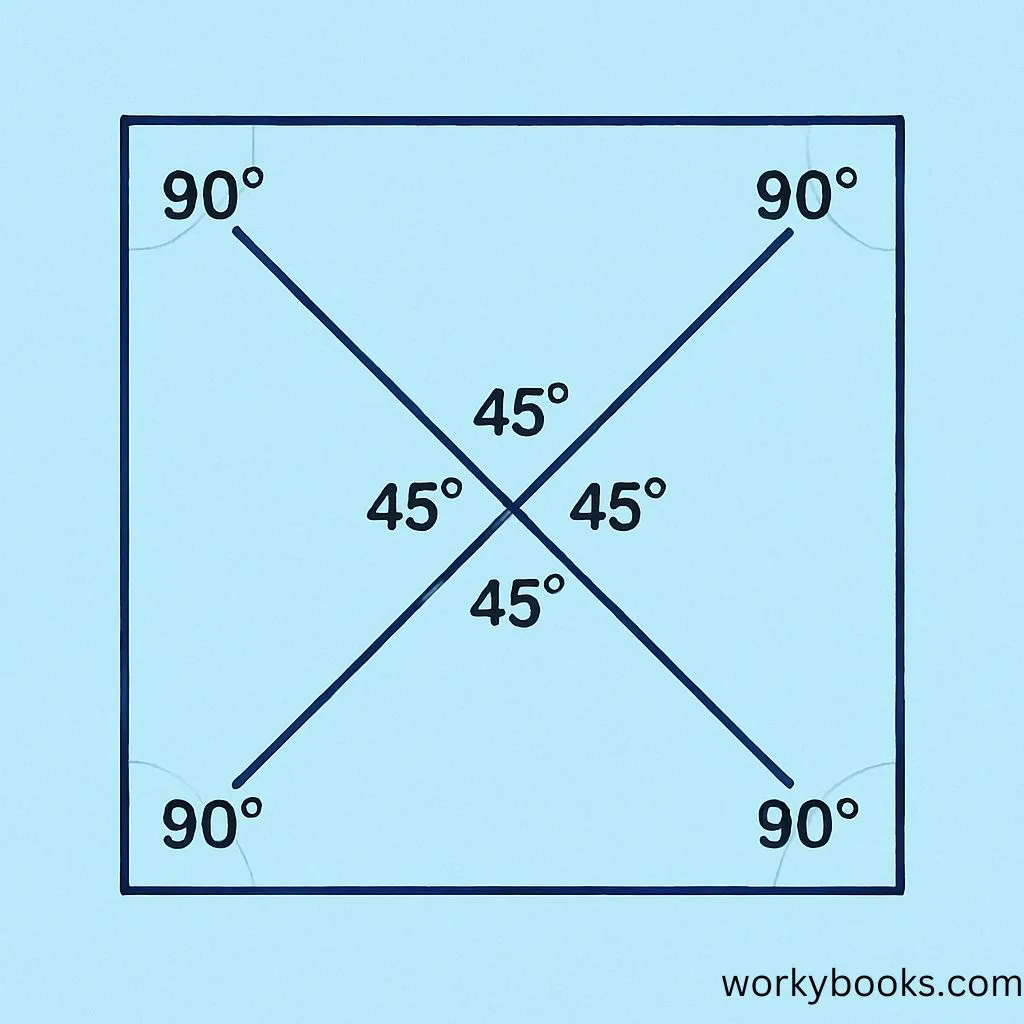
Square diagonals have several important properties that make them special:
1. Equal Length: Both diagonals are always the same length
2. Perpendicular: They cross at right angles (90 degrees)
3. Bisect Each Other: Each diagonal cuts the other into two equal parts at the center
4. Bisect Angles: Each diagonal divides the corner angles into two equal 45-degree angles
These properties are unique to squares and help us solve geometry problems.
Remember
In a square, diagonals are always longer than the sides and always meet at the exact center.
Diagonal Formula
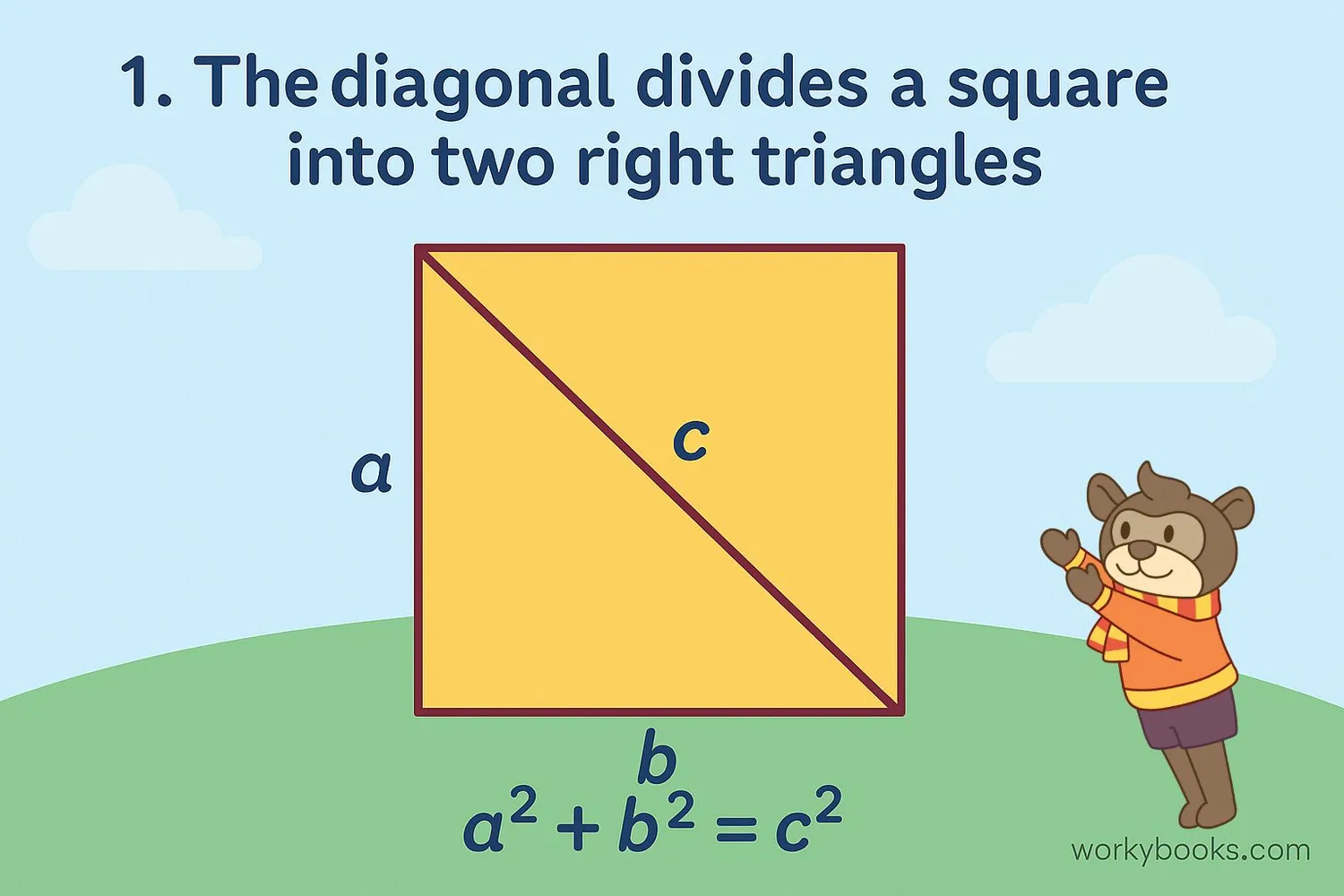
We can calculate the length of a diagonal using a simple formula based on the Pythagorean theorem:
Diagonal Formula
Where d is the diagonal length and s is the side length
When you draw a diagonal in a square, it creates two right triangles. Each triangle has:
- Two sides equal to the square's side length (s)
- A hypotenuse equal to the diagonal (d)
Formula Tip
To find the diagonal length, multiply the side length by the square root of 2 (about 1.414).
Examples
Let's practice using the diagonal formula with some examples:
Example 1: A square has sides of 5 cm. What is its diagonal length?
Solution: d = s × √2 = 5 × 1.414 ≈ 7.07 cm
Example 2: A square chessboard has a diagonal of 50 cm. How long are its sides?
Solution: d = s × √2 → 50 = s × 1.414 → s = 50 ÷ 1.414 ≈ 35.36 cm
Example 3: A square picture frame has sides of 30 cm. What diagonal measurement would fit it?
Solution: d = 30 × √2 ≈ 30 × 1.414 = 42.42 cm
Example 4: A square tile has a diagonal of 14.14 cm. What is its side length?
Solution: Since d = s × √2, then s = d ÷ √2 = 14.14 ÷ 1.414 = 10 cm
Practice Tip
Notice that when side length doubles, diagonal length also doubles. The ratio always stays the same: d/s = √2
Practice Quiz
Test your knowledge about square diagonals with these questions:
Frequently Asked Questions
Here are answers to common questions about square diagonals:
Geometry Trivia
Discover interesting facts about squares and diagonals:
Ancient Knowledge
The Babylonians understood the relationship between a square's side and diagonal around 1800 BCE. Their clay tablets show calculations equivalent to √2 accurate to six decimal places!
Irrational Discovery
The diagonal of a square led to the discovery of irrational numbers. Ancient Greek mathematicians proved that √2 cannot be expressed as a fraction, revolutionizing mathematics.
Architectural Use
Builders use square diagonals to ensure perfect right angles. If both diagonals of a rectangular frame are equal, all corners are exactly 90 degrees - a technique used since ancient times.
Crystal Structures
Square patterns with diagonals appear in crystal structures. Salt crystals form cubic shapes where diagonals connect atoms in a repeating pattern found throughout nature.





