Diagonals of a Parallelogram - Definition, Examples, Quiz, FAQ, Trivia
Learn about the special properties of parallelogram diagonals with visual examples and practice activities
What is a Diagonal?
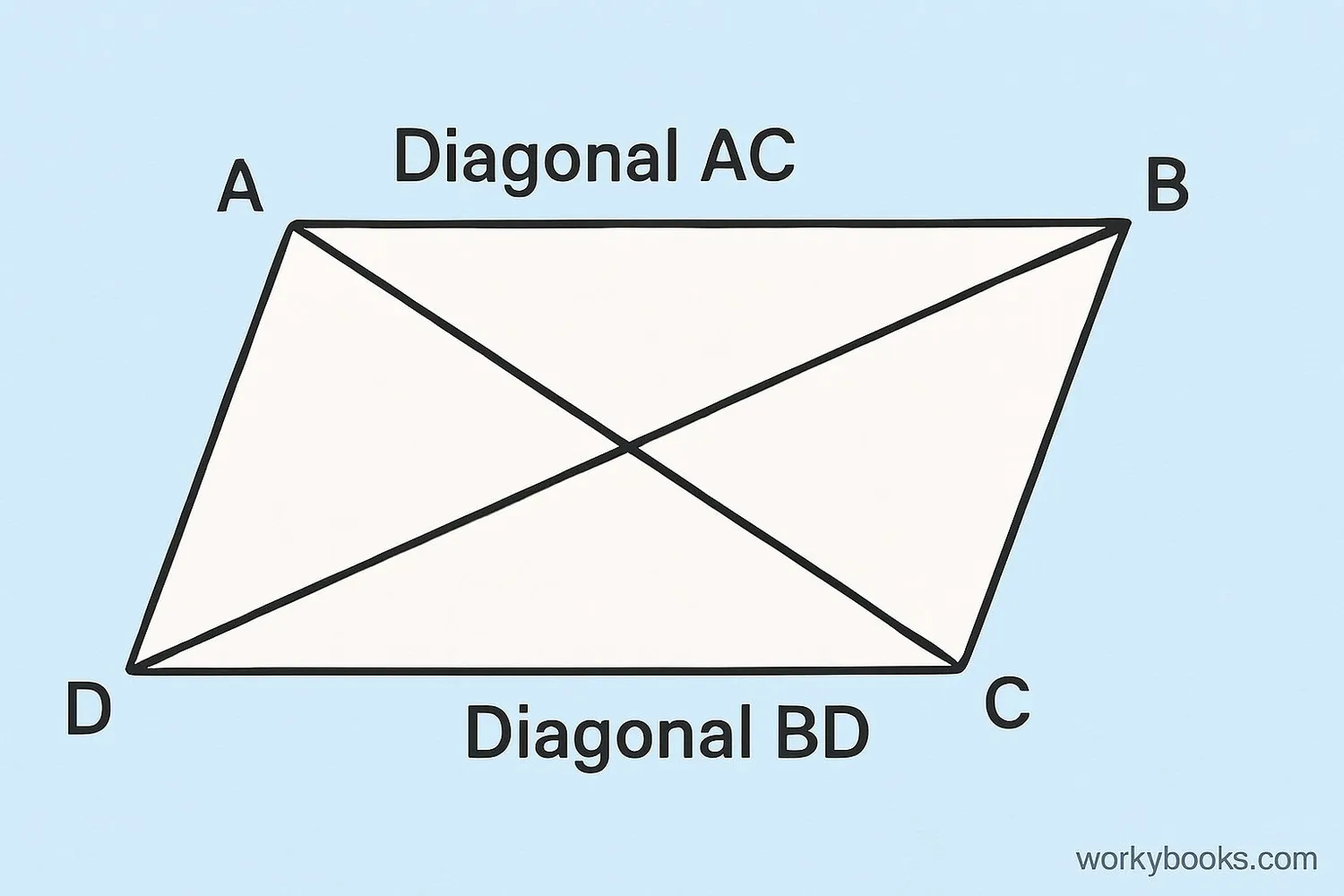
A diagonal is a line segment that connects two opposite corners (vertices) of a shape. In a parallelogram, which is a four-sided shape with opposite sides that are parallel and equal in length, there are two diagonals.
Diagonals are important because they reveal special properties about the parallelogram. When you draw both diagonals in a parallelogram, they create interesting patterns and have special relationships with each other.
Unlike regular quadrilaterals, parallelograms have diagonals that behave in predictable ways. Understanding these diagonals helps us solve geometry problems and recognize special types of parallelograms.
Key Concept
Every parallelogram has two diagonals that cross each other at a single point.
Properties of Diagonals
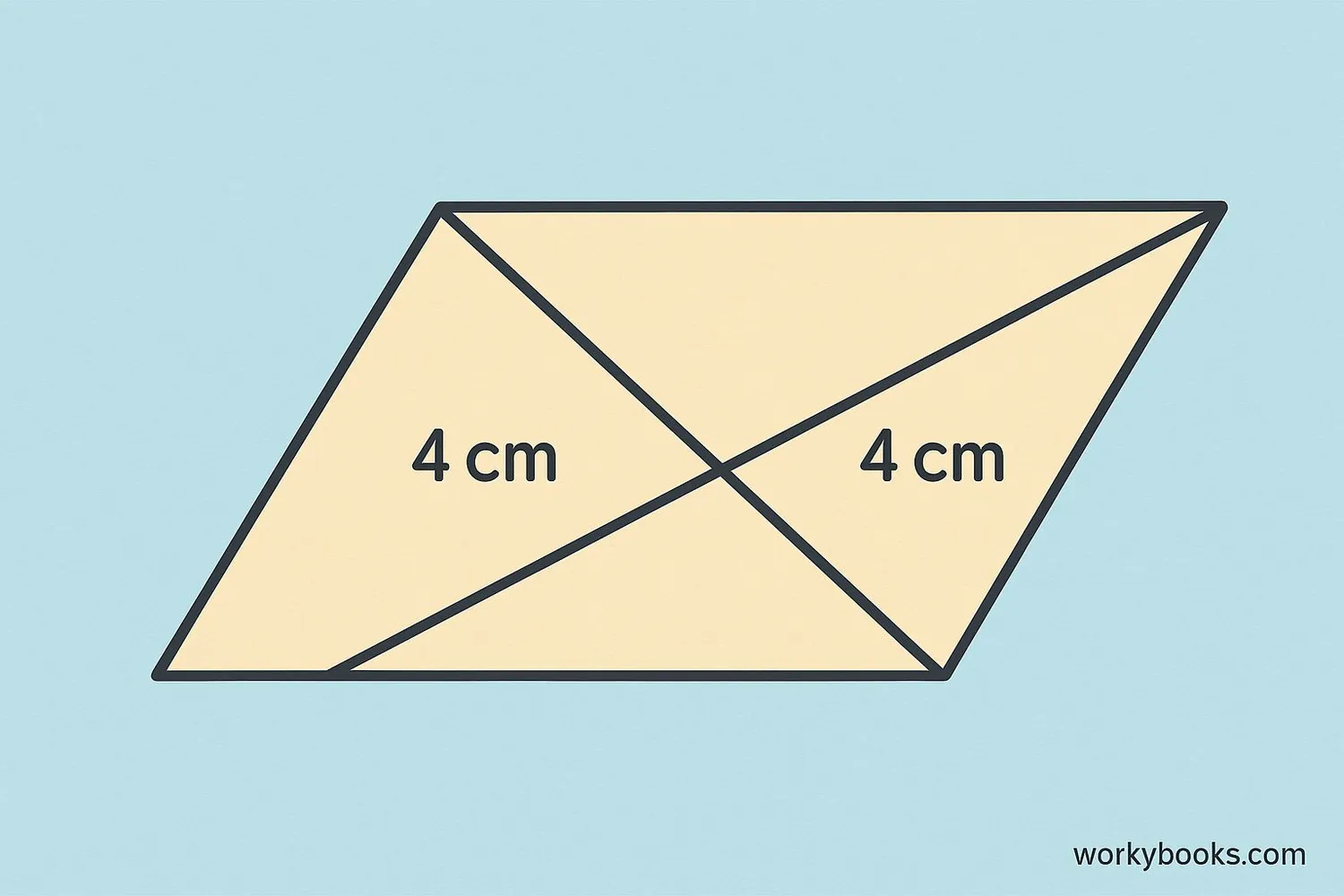
The diagonals of a parallelogram have two important properties:
Bisecting Property
The diagonals of a parallelogram bisect each other. This means they cut each other exactly in half at the point where they cross.
Division Property
Each diagonal divides the parallelogram into two congruent triangles. This means the two triangles are exactly the same size and shape.
In a rectangle, the diagonals have an additional property: they are equal in length. This is what gives rectangles their distinctive shape.
Remember
In any parallelogram, the diagonals always bisect each other, but they are only equal in rectangles and squares.
Special Parallelograms
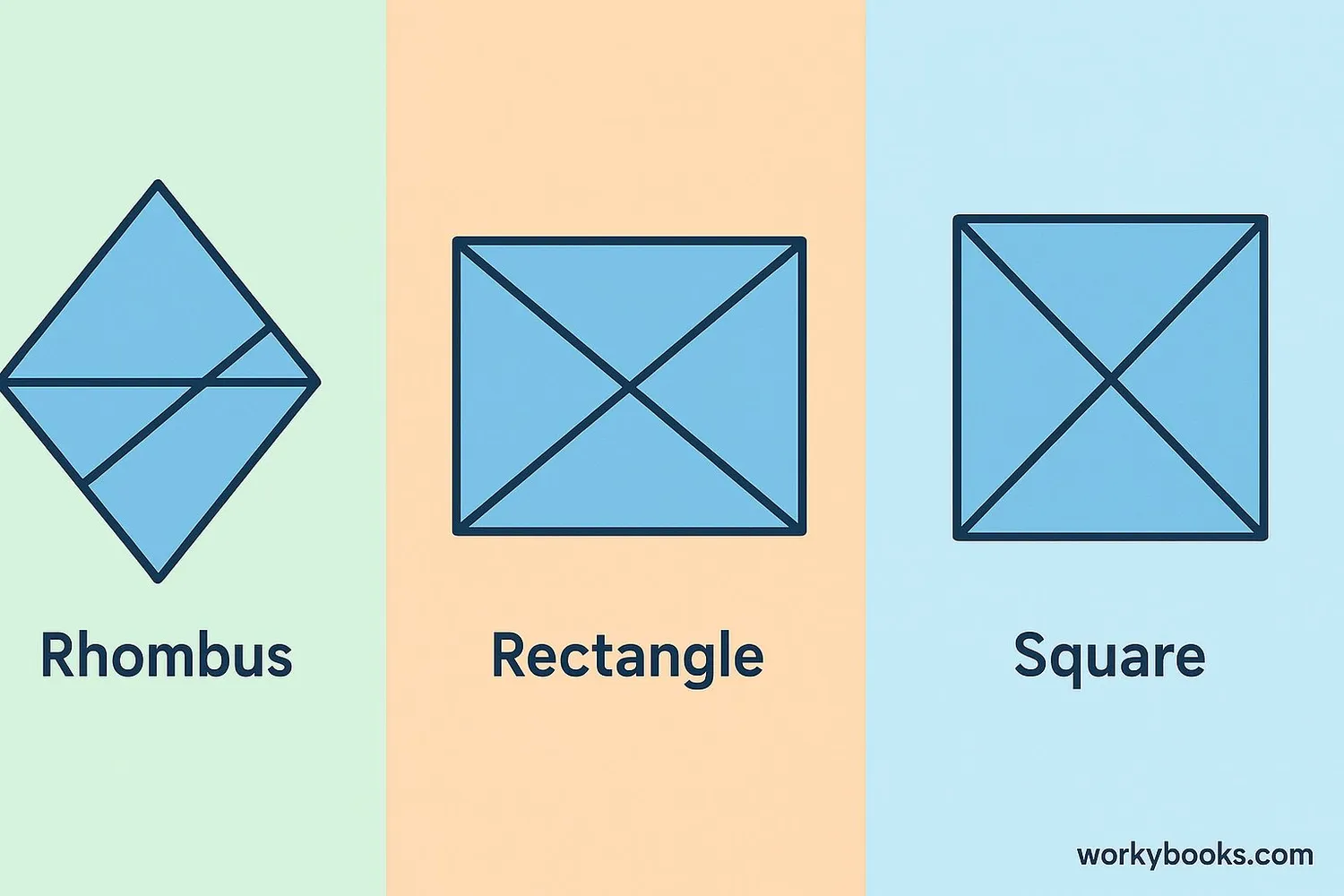
Some parallelograms have extra special diagonal properties:
Rhombus
In a rhombus (all sides equal), the diagonals are perpendicular to each other and bisect the vertex angles. They are not equal in length.
Rectangle
In a rectangle (all angles 90°), the diagonals are equal in length but not necessarily perpendicular to each other.
Square
In a square (all sides equal and all angles 90°), the diagonals are equal in length and perpendicular to each other. They also bisect the vertex angles.
- If a parallelogram has perpendicular diagonals, it must be a rhombus or a square.
- If a parallelogram has equal diagonals, it must be a rectangle or a square.
This is why squares have all the properties of both rhombuses and rectangles!
Pattern
The more special properties a parallelogram has, the more special diagonal properties it will have too!
Real-World Examples
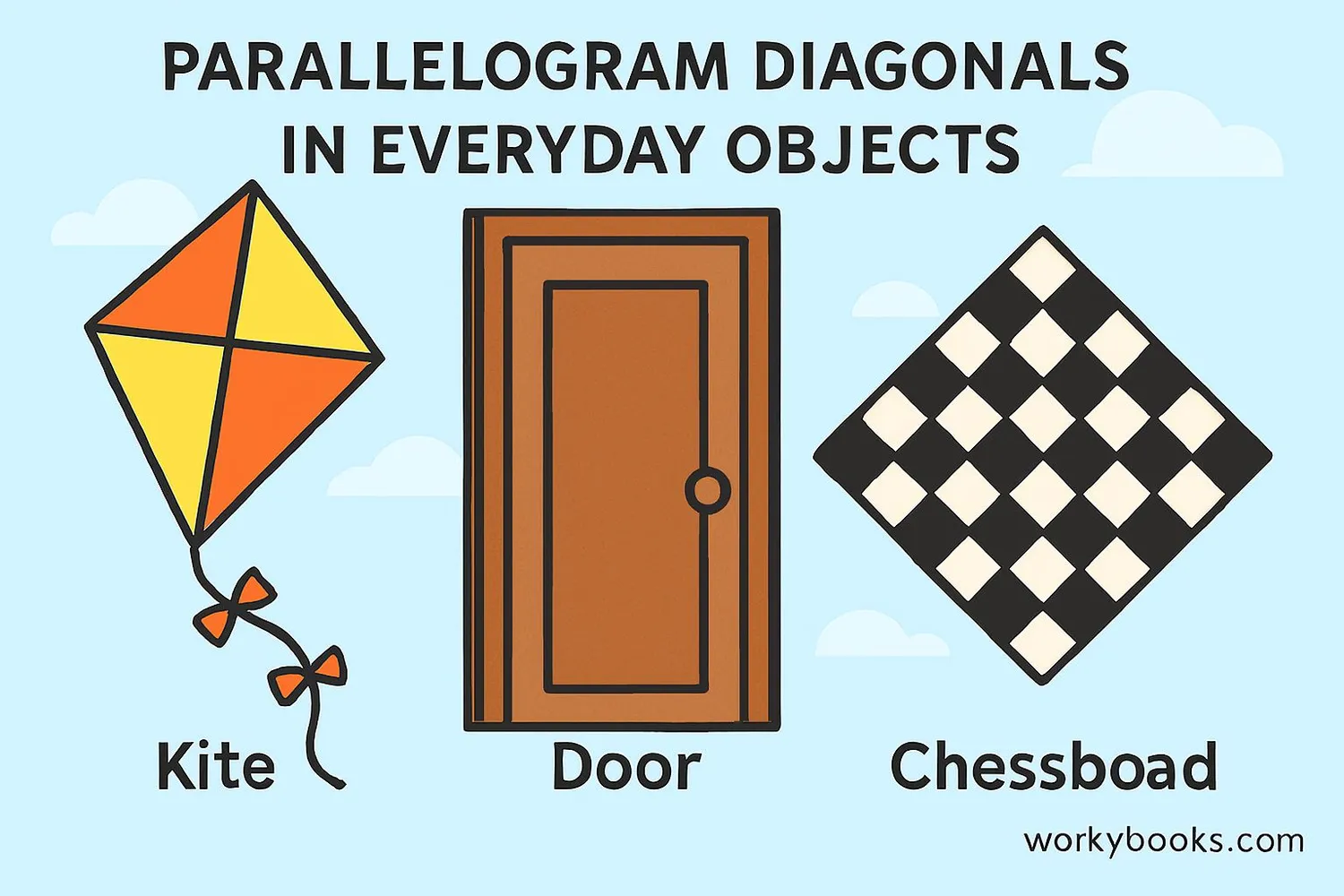
Let's see how parallelogram diagonals appear in the real world:
Example 1: Kite (Rhombus)
A kite shaped like a rhombus has two perpendicular diagonals. The longer diagonal bisects the shorter one at a 90° angle.
Example 2: Door Frame (Rectangle)
The diagonals of a door frame are equal in length. If you measure from top-left to bottom-right and top-right to bottom-left, the measurements will be equal.
Example 3: Chess Board (Square)
A chess board has diagonals that are equal in length and cross at 90° angles. Each diagonal also bisects the corners of the squares.
Example 4: Picture Frame
When you add a diagonal brace to a picture frame, you're using the property that triangles are rigid. Each diagonal divides the frame into two triangles.
Practice finding parallelograms around you - tiles, windows, book covers, and more!
Application
Carpenters use the property that rectangle diagonals are equal to check if a frame is perfectly rectangular.
Practice Quiz
Test your knowledge about parallelogram diagonals with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about parallelogram diagonals:
Geometry Trivia
Discover interesting facts about parallelograms and diagonals:
Ancient Discovery
The properties of parallelogram diagonals were first described by Greek mathematician Euclid around 300 BCE in his work "Elements".
Engineering Applications
Parallelogram properties are used in engineering for structures like bridges and cranes, where diagonal braces add stability.
3D Shapes
In 3D geometry, the concept of diagonals extends to parallelepipeds (3D parallelograms), which have space diagonals connecting opposite vertices.
Measurement Standard
The property that rectangle diagonals are equal is used by builders worldwide to ensure structures have perfect right angles.





