Dimensions - Definition, Examples, Quiz, FAQ, Trivia
Learn about zero-dimensional, one-dimensional, two-dimensional and three-dimensional concepts
What is Dimension in Math?
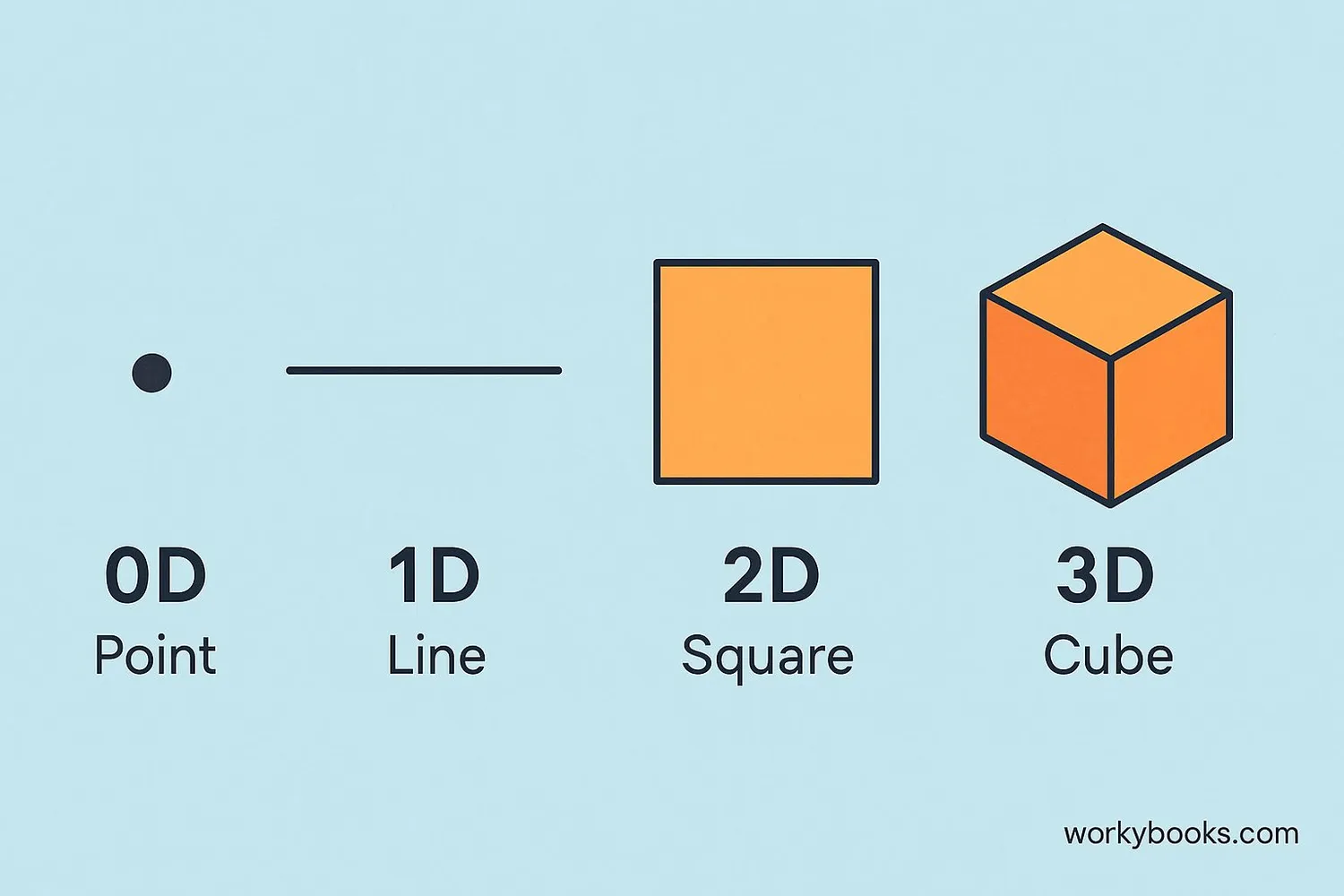
In math, dimension refers to the number of coordinates needed to specify any point within a space. It tells us how many directions we can move in that space. For example:
0D (Zero-dimensional): A single point with no size or direction. You can't move anywhere from a point.
1D (One-dimensional): A straight line where you can move only forward or backward.
2D (Two-dimensional): A flat surface like paper where you can move up/down and left/right.
3D (Three-dimensional): The space we live in where you can move up/down, left/right, and forward/backward.
Dimensions help us understand the world around us and solve problems in mathematics, science, and engineering.
Key Concept
The dimension of a space is the number of independent directions needed to move within that space.
Types of Dimensions
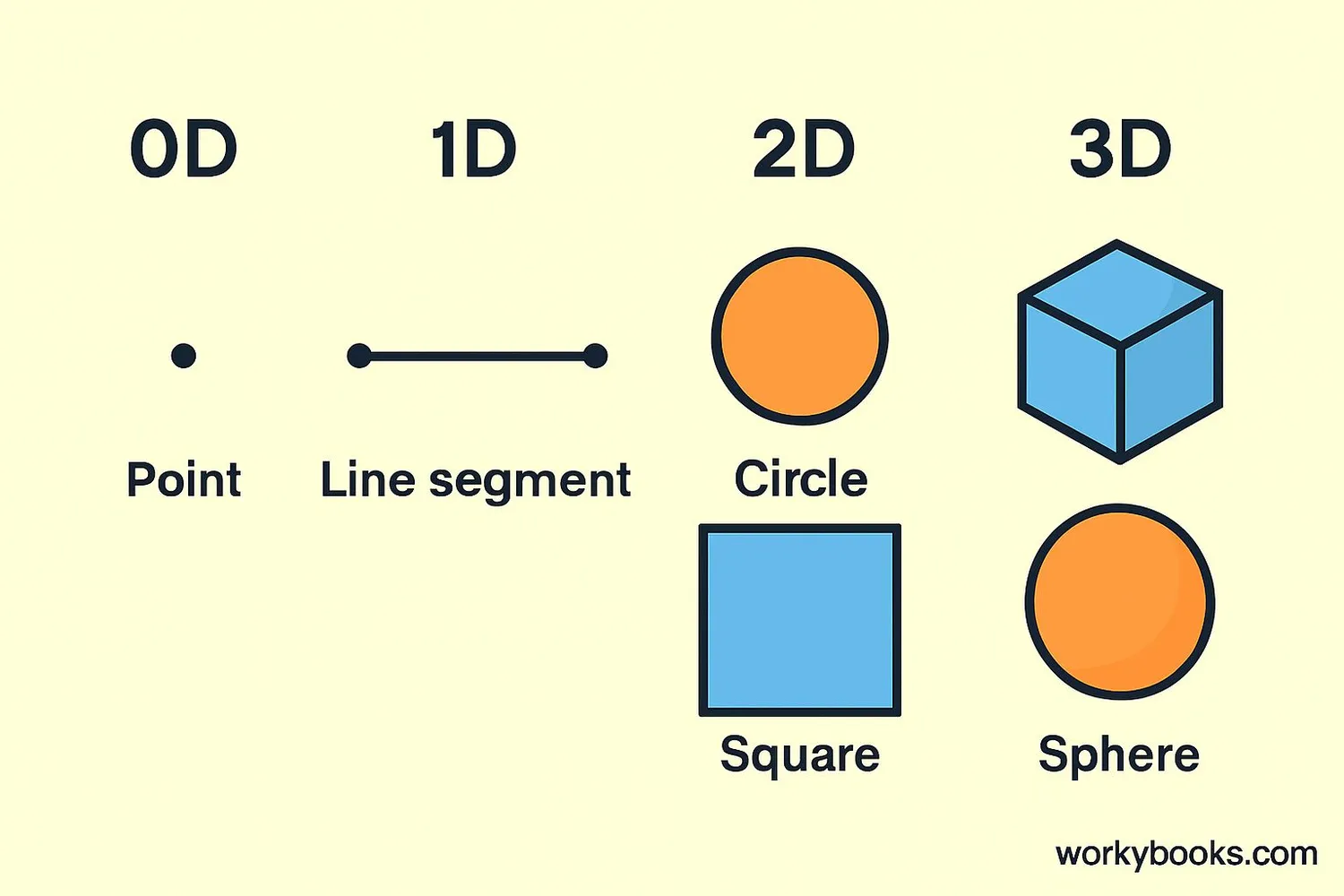
Zero-Dimensional (0D)
A point with no length, width, or height. It only has a position.
- Example: A dot on paper
- Has no size or direction
- Represented by coordinates (x,y,z)
One-Dimensional (1D)
A straight line with length but no width or height.
- Example: A straight line segment
- Has length but no area
- Can be measured in one direction
Two-Dimensional (2D)
Flat shapes with length and width but no height.
- Examples: Circle, square, triangle
- Have area but no volume
- Can be measured in two directions
Three-Dimensional (3D)
Solid objects with length, width, and height.
- Examples: Cube, sphere, pyramid
- Have volume and surface area
- Can be measured in three directions
Remember
Dimensions build on each other: A point (0D) can create a line (1D), which can create a surface (2D), which can create a solid (3D).
Two-Dimensional Shapes (2D)
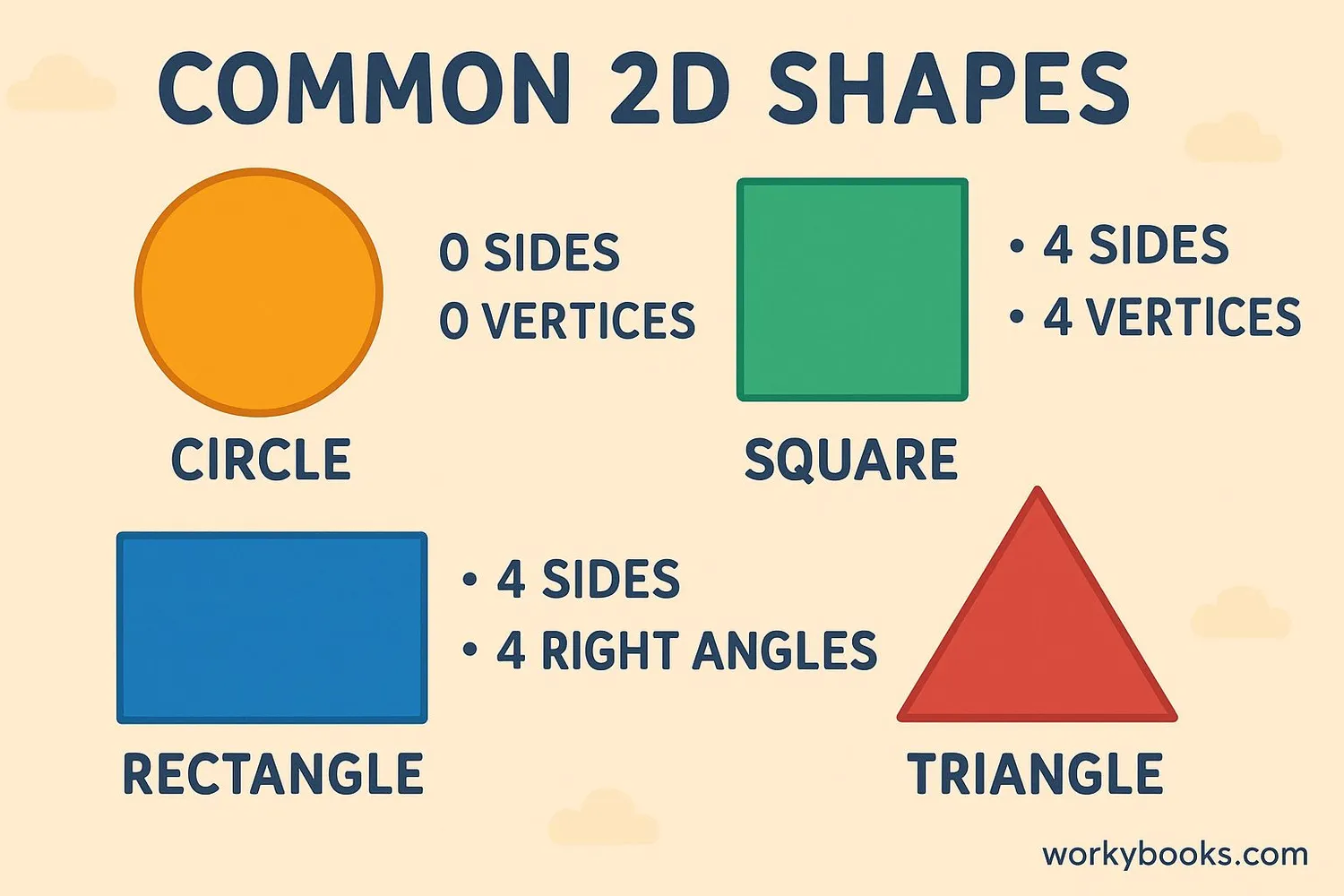
Two-dimensional shapes are flat figures that have length and width but no height. They are also called plane shapes. We can measure two important properties of 2D shapes:
Perimeter: The total distance around the shape. It's like walking around the edge of the shape.
Area: The amount of space inside the shape. It's like painting the inside of the shape.
Here are some common 2D shapes:
Circle
A round shape with no corners. All points are the same distance from the center.
Square
Has four equal sides and four right angles (90°).
Rectangle
Has four sides with opposite sides equal and four right angles.
Triangle
Has three sides and three angles. The sum of angles is always 180°.
Real-World Connection
2D shapes are everywhere! Paper, screens, paintings, and maps are all two-dimensional surfaces.
Three-Dimensional Shapes (3D)

Three-dimensional shapes are solid objects that have length, width, and height. They are also called solid shapes. We can measure two important properties of 3D shapes:
Volume: The amount of space inside the shape. Measured in cubic units (like cubic centimeters or cubic meters).
Surface Area: The total area of all the faces of the shape. Measured in square units.
Here are some common 3D shapes:
Cube
Has 6 square faces, 12 edges, and 8 vertices. All faces are equal.
Sphere
A perfectly round ball with no edges or vertices. All points are the same distance from the center.
Cylinder
Has two circular faces and one curved surface. Like a can of soup.
Cone
Has one circular base and one curved surface that tapers to a point.
Real-World Connection
3D shapes are all around us! Books are cuboids, balls are spheres, and ice cream cones are... well, cones!
Key Concepts
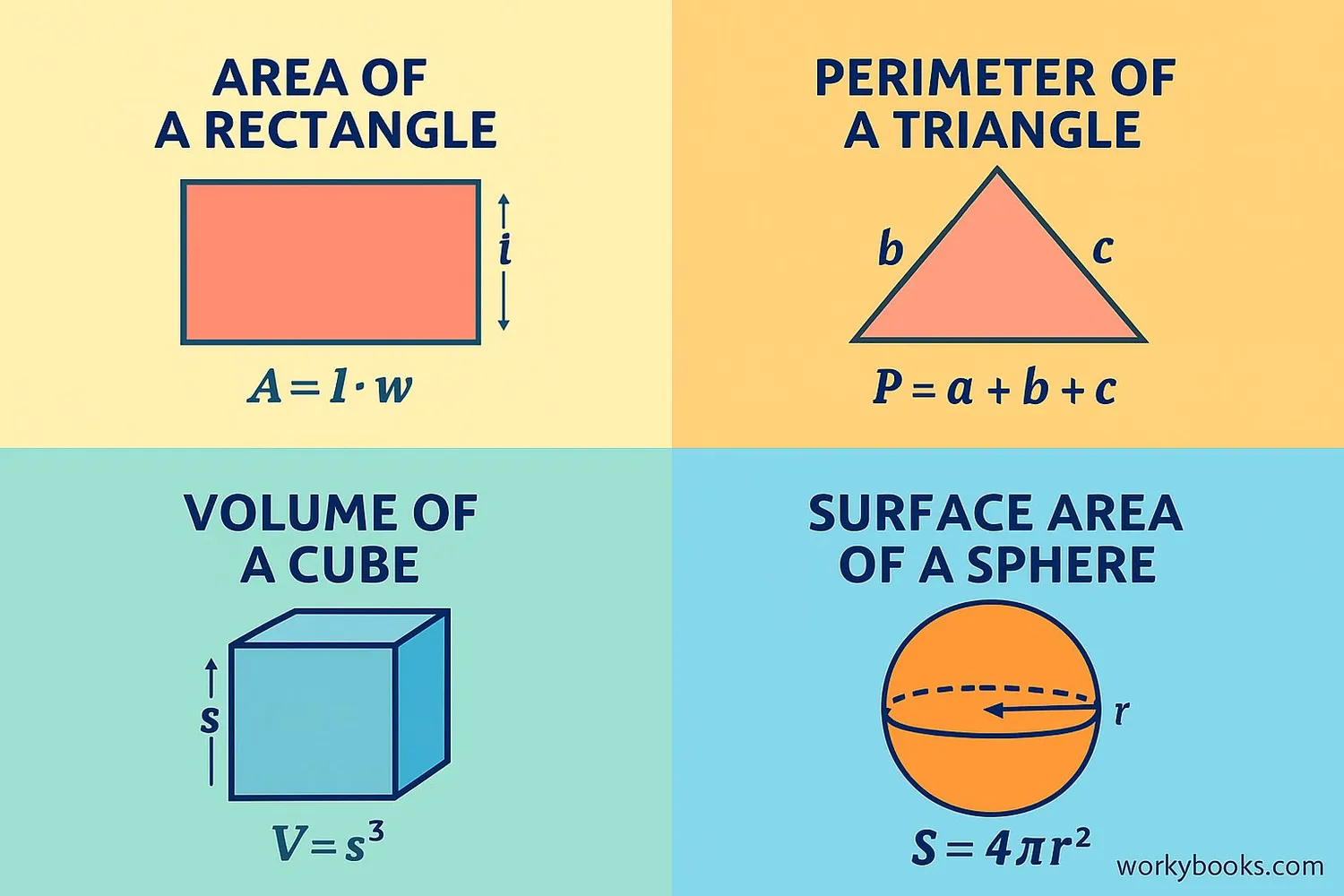
Understanding dimensions involves knowing these important mathematical concepts:
Perimeter
The distance around a 2D shape. For a rectangle: P = 2 × (length + width)
Area
The space inside a 2D shape. For a rectangle: A = length × width
Volume
The space inside a 3D shape. For a cube: V = side × side × side
Surface Area
The total area of all faces of a 3D shape. For a cube: SA = 6 × side²
Remember
Perimeter and area are for 2D shapes, while volume and surface area are for 3D shapes.
Dimensions Quiz
Test your knowledge about dimensions with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about dimensions in math:
Math Dimensions Trivia
Discover interesting facts about dimensions in mathematics:
Ancient Dimensions
Ancient Egyptians were using two-dimensional geometry as early as 3000 BC to measure land areas after Nile River floods. Their understanding helped develop early geometry.
Fourth Dimension
Albert Einstein's theory of relativity treats time as the fourth dimension. This concept helps explain how space and time are connected in our universe.
String Theory
Some physicists believe our universe might have more than three dimensions. String theory suggests there could be 10 or 11 dimensions!
Largest 3D Model
The largest 3D-printed structure is a 25-foot, 3D-printed rocket made in 2023. It shows how we use 3D concepts in modern technology.





