Dividing Mixed Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn to divide mixed numbers with step-by-step instructions, visual examples, and practice activities
What are Mixed Numbers?
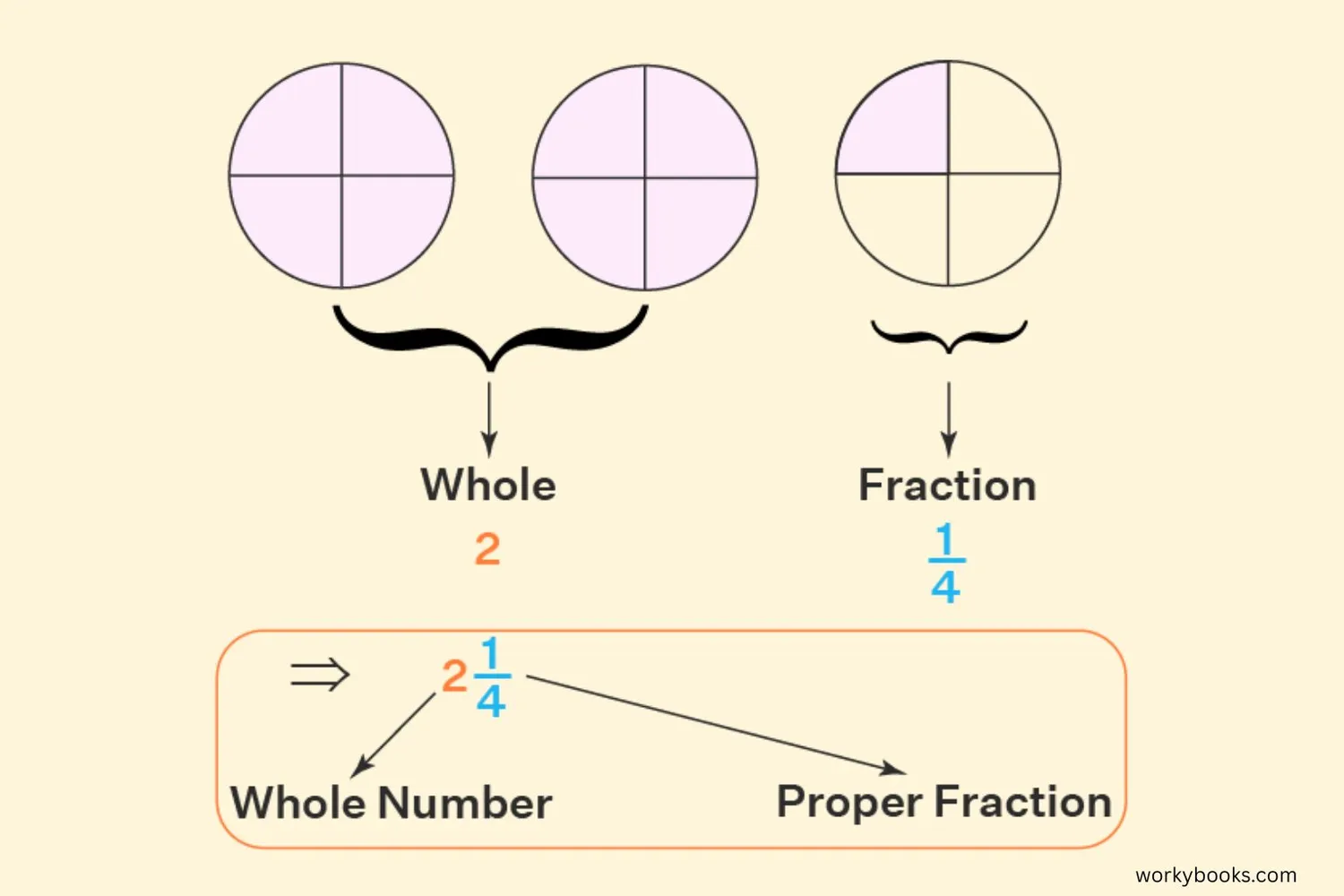
A mixed number is a combination of a whole number and a proper fraction. For example, 2½ (two and one-half) is a mixed number. The whole number part is 2, and the fractional part is ½.
Mixed numbers represent quantities that are more than a whole but not a complete set of wholes. We encounter mixed numbers in daily life when measuring ingredients, describing lengths, or talking about time.
Before we can divide mixed numbers, we need to convert them to improper fractions. An improper fraction has a numerator that is larger than its denominator, like 5/4.
Key Concept
Mixed numbers combine whole numbers and fractions. To work with them in division, we first convert them to improper fractions.
How to Divide Mixed Numbers

Dividing mixed numbers might seem tricky, but it becomes easy when you follow these steps:
Convert to Improper Fractions
Change each mixed number to an improper fraction. Multiply the whole number by the denominator, then add the numerator. Keep the same denominator.
Keep, Change, Flip
Keep the first fraction, change the division sign to multiplication, and flip the second fraction (find its reciprocal).
Multiply the Fractions
Multiply the numerators together and the denominators together.
Simplify
Simplify your answer by reducing the fraction to lowest terms. If it's an improper fraction, you may convert it back to a mixed number.
Remember
Division of fractions is the same as multiplying by the reciprocal. The reciprocal of a fraction is created by flipping its numerator and denominator.
Examples
Let's practice dividing mixed numbers with some examples:
Step 1: Convert to improper fractions:
2½ = (2×2 + 1)/2 = 5/2
1¼ = (1×4 + 1)/4 = 5/4
Step 2: Keep, change, flip:
5/2 ÷ 5/4 becomes 5/2 × 4/5
Step 3: Multiply numerators and denominators:
(5×4)/(2×5) = 20/10
Step 4: Simplify:
20/10 = 2
Answer: 2½ ÷ 1¼ = 2
Step 1: Convert to improper fractions:
3⅓ = (3×3 + 1)/3 = 10/3
2¼ = (2×4 + 1)/4 = 9/4
Step 2: Keep, change, flip:
10/3 ÷ 9/4 becomes 10/3 × 4/9
Step 3: Multiply numerators and denominators:
(10×4)/(3×9) = 40/27
Step 4: Simplify and convert to mixed number:
40/27 = 1¹³⁄₂₇
Answer: 3⅓ ÷ 2¼ = 1¹³⁄₂₇
Step 1: Convert mixed number to improper fraction and write whole number as fraction:
4¾ = (4×4 + 3)/4 = 19/4
2 = 2/1
Step 2: Keep, change, flip:
19/4 ÷ 2/1 becomes 19/4 × 1/2
Step 3: Multiply numerators and denominators:
(19×1)/(4×2) = 19/8
Step 4: Simplify and convert to mixed number:
19/8 = 2⅜
Answer: 4¾ ÷ 2 = 2⅜
Practice Tip
Always double-check that you've converted mixed numbers to improper fractions correctly before proceeding with division.
Practice Quiz
Test your understanding of dividing mixed numbers with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about dividing mixed numbers:
Math Trivia
Discover interesting facts about fractions and mathematics:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they primarily used unit fractions (fractions with 1 as the numerator). They would express other fractions as sums of unit fractions.
Fraction Origins
The word "fraction" comes from the Latin word "fractus" which means "broken." This makes sense because fractions represent parts of a whole—like a broken piece of something.
Fractions in Nature
Fractions appear throughout nature! The patterns of sunflower seeds, pinecones, and even the branching of trees often follow the Fibonacci sequence, which creates fractional relationships.
Musical Fractions
Musical notes are based on fractions. A whole note can be divided into half notes, quarter notes, eighth notes, and so on. The time signature in music is actually a fraction!





