Divisible - Definition, Examples, Quiz, FAQ, Trivia
Learn about divisibility with easy explanations, rules, examples, and practice activities
What Does Divisible Mean?
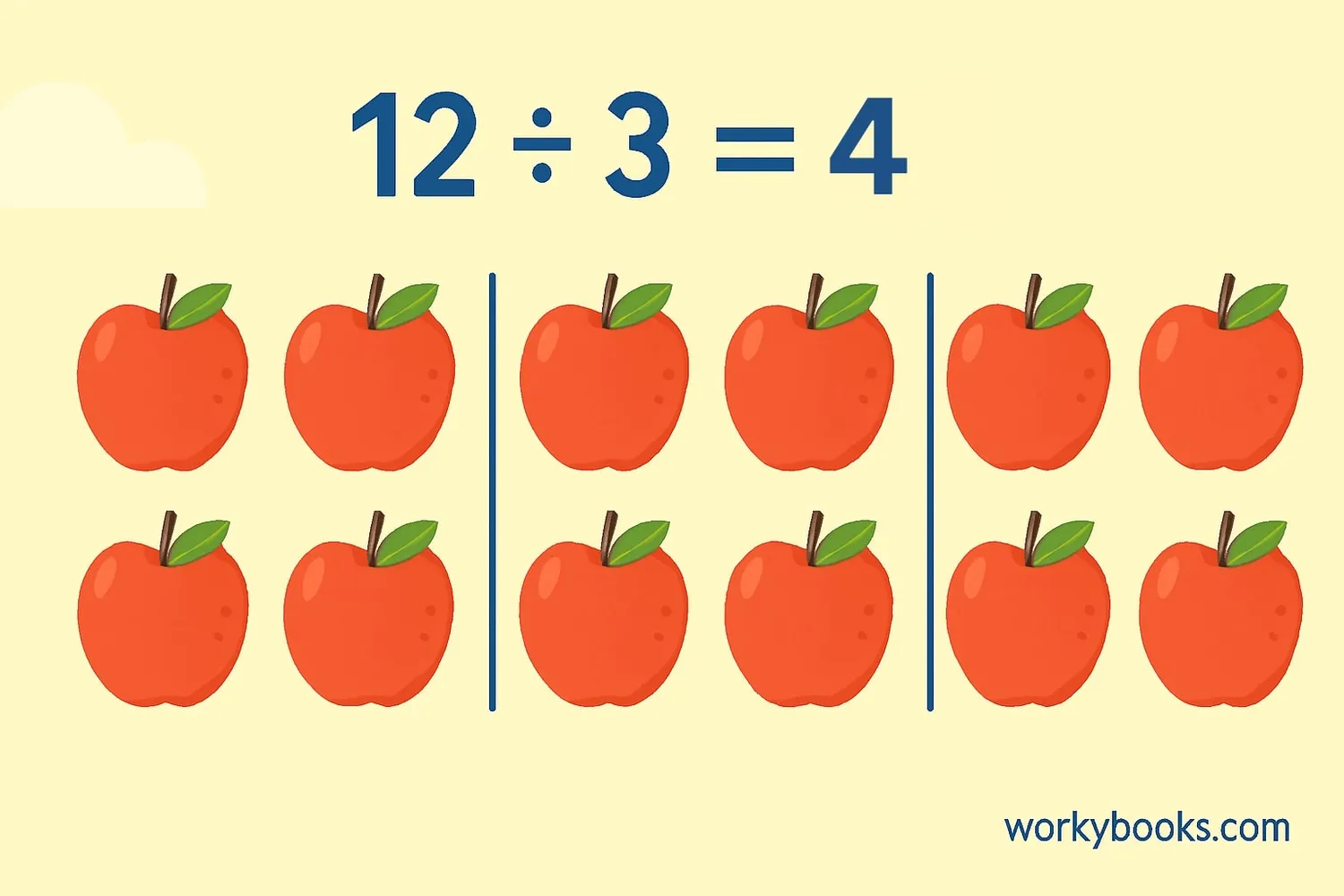
In math, when we say a number is divisible by another number, it means it can be divided exactly with no remainder.
For example, 12 is divisible by 3 because 12 ÷ 3 = 4 exactly. There's nothing left over. But 12 is not divisible by 5 because 12 ÷ 5 = 2 with a remainder of 2.
Think of it like sharing cookies fairly with friends. If you have 12 cookies and 3 friends, each friend gets exactly 4 cookies. But if you have 12 cookies and 5 friends, you can't share them equally without breaking cookies or having some left over.
Key Definition
If a number (a) can be divided by another number (b) to give a whole number (c) with no remainder, then a is divisible by b.
Key Concept
Divisible means a number can be divided exactly by another number with no remainder left over.
Divisibility Rules

Divisibility rules are shortcuts that help us quickly determine if one number is divisible by another without doing the full division. Here are the most important rules:
Divisible by 2
A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
Example: 34, 76, 90, and 102 are all divisible by 2.
Divisible by 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
Example: 123 (1+2+3=6, which is divisible by 3).
Divisible by 4
A number is divisible by 4 if its last two digits form a number divisible by 4.
Example: 312 (12 is divisible by 4).
Divisible by 5
A number is divisible by 5 if its last digit is 0 or 5.
Example: 75, 90, and 105 are all divisible by 5.
Divisible by 6
A number is divisible by 6 if it is divisible by both 2 and 3.
Example: 48 (even and 4+8=12, divisible by 3).
Divisible by 9
A number is divisible by 9 if the sum of its digits is divisible by 9.
Example: 918 (9+1+8=18, divisible by 9).
Divisible by 10
A number is divisible by 10 if it ends with a 0.
Example: 70, 120, and 350 are all divisible by 10.
Remember
These rules are helpful shortcuts, but you can always check divisibility by doing the actual division to see if there's a remainder.
Examples of Divisibility
Let's practice identifying divisible numbers with some examples:
Example 1: Is 48 divisible by 4?
Solution: Check the last two digits - 48. Since 48 ÷ 4 = 12 with no remainder, yes, 48 is divisible by 4.
Example 2: Is 135 divisible by 3?
Solution: Add the digits: 1 + 3 + 5 = 9. Since 9 is divisible by 3, yes, 135 is divisible by 3.
Example 3: Is 250 divisible by 10?
Solution: Check the last digit - it's 0, so yes, 250 is divisible by 10.
Example 4: Is 72 divisible by 6?
Solution: Check if it's divisible by both 2 and 3. 72 is even (divisible by 2) and 7+2=9 (divisible by 3), so yes, 72 is divisible by 6.
Example 5: Is 91 divisible by 7?
Solution: 91 ÷ 7 = 13 exactly, with no remainder, so yes, 91 is divisible by 7.
Practice Tip
Try testing divisibility with numbers you encounter in daily life - page numbers, your age, the number of students in your class!
Divisibility Practice Quiz
Test your divisibility knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about divisibility:
Math Trivia
Discover interesting facts about numbers and divisibility:
Ancient Divisibility
The ancient Babylonians were using divisibility rules as early as 2000 BCE! They had a base-60 number system (sexagesimal) which is why we have 60 seconds in a minute and 60 minutes in an hour.
Perfect Numbers
A perfect number is a number that equals the sum of its proper divisors (numbers that divide it exactly). The smallest perfect number is 6, because its divisors are 1, 2, and 3, and 1 + 2 + 3 = 6.
Divisibility in Nature
Many patterns in nature follow divisibility rules. For example, the number of petals on flowers often follows numbers in the Fibonacci sequence, which has interesting divisibility properties.
Largest Prime
The largest known prime number has over 24 million digits! Prime numbers are only divisible by 1 and themselves, making them the building blocks of all numbers.





