Dodecagon - Definition, Examples, Quiz, FAQ, Trivia
Learn about polygons with twelve sides, their properties, and where we see them in the world
What is a Dodecagon?
A dodecagon is a polygon with 12 sides and 12 angles. The word comes from Greek words: "dodeka" meaning twelve and "gonia" meaning angle.
All dodecagons have:
- 12 straight sides
- 12 vertices (corners where sides meet)
- 12 interior angles
- 12 exterior angles
Dodecagons are found in nature, architecture, and everyday objects. They belong to the family of polygons that includes triangles (3 sides), quadrilaterals (4 sides), pentagons (5 sides), and so on.
Key Concept
All polygons with 12 sides are dodecagons, but they can have different shapes depending on their angles and side lengths.
Types of Dodecagons

Dodecagons come in different forms based on their sides and angles:
Regular Dodecagon: All 12 sides are equal length, and all 12 angles are equal (150° each). This is the most symmetrical type.
Irregular Dodecagon: Sides and angles are not all equal. This is the most common type in real life.
Convex Dodecagon: All interior angles are less than 180°, and all vertices point outward.
Concave Dodecagon: At least one interior angle is greater than 180°, creating a "caved-in" appearance.
Skew Dodecagon: A 3D version where the sides are not all in the same plane.
Remember
Regular dodecagons are perfectly symmetrical, while irregular ones can have sides and angles of different lengths and measures.
Properties of a Dodecagon
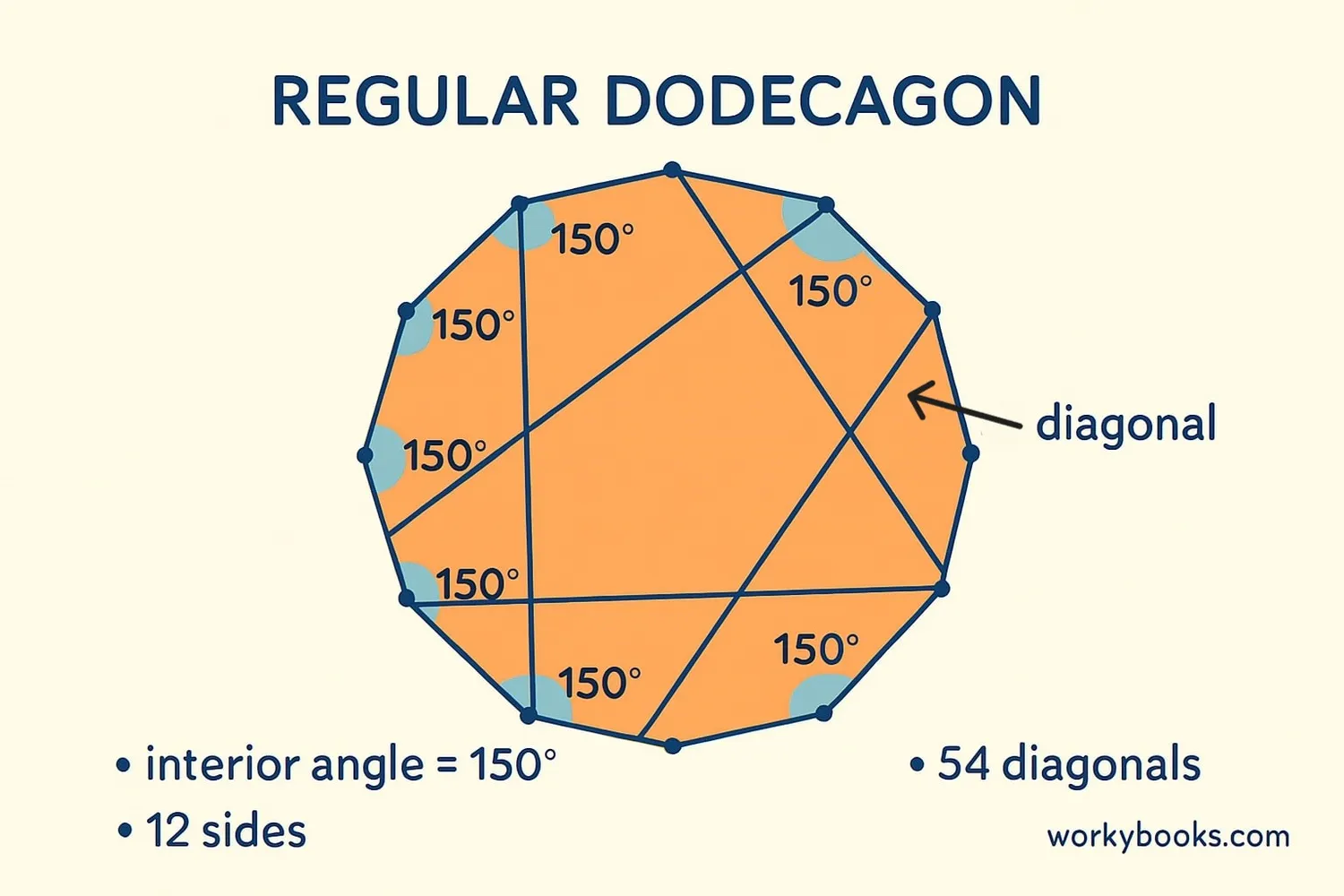
Sides
All dodecagons have twelve straight sides
Vertices
Points where sides meet
Interior Angles
Each angle in a regular dodecagon
Exterior Angles
Each exterior angle in a regular dodecagon
Diagonals
Total diagonals in a convex dodecagon
Sum of Interior Angles
Total degrees inside a dodecagon
Key Formulas:
Sum of Interior Angles: (n-2) × 180° = (12-2) × 180° = 10 × 180° = 1800°
Each Interior Angle (Regular): Sum ÷ n = 1800° ÷ 12 = 150°
Each Exterior Angle (Regular): 360° ÷ n = 360° ÷ 12 = 30°
Number of Diagonals: n(n-3)/2 = 12(12-3)/2 = (12×9)/2 = 54
Area & Perimeter
For regular dodecagons (where all sides are equal), we can calculate area and perimeter:
Perimeter Formula
Where s is the length of one side
Area Formula
Where s is the length of one side
For a regular dodecagon with side length 5 cm:
Perimeter: 12 × 5 = 60 cm
Area: 3 × (2 + √3) × 5² ≈ 3 × (2 + 1.732) × 25 ≈ 3 × 3.732 × 25 ≈ 279.9 cm²
Remember
These formulas only work for regular dodecagons. For irregular dodecagons, we divide them into smaller shapes to calculate area.
Real-World Examples

Dodecagons appear in many places around us:
Coins: Some coins like the British One Pound coin have 12 sides
Clock Faces: Traditional clocks often show 12 hours
Architecture: Some buildings and windows have dodecagonal shapes
Games: Dice with 12 sides (dodecahedrons)
Nature: Certain crystals and rock formations have 12-sided shapes
Art: Patterns in quilts, tiles, and mosaics often use dodecagons
Did You Know?
The dodecahedron is a 3D shape with 12 pentagonal faces. Plato associated it with the universe!
Practice Quiz
Test your knowledge about dodecagons with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about dodecagons:
Dodecagon Trivia
Discover interesting facts about dodecagons:
Ancient Geometry
The regular dodecagon was studied by ancient Greek mathematicians. Euclid described how to construct one using only a compass and straightedge in his book "Elements".
Carbon Molecules
Some carbon molecules form dodecahedral structures. The C20 molecule is shaped like a dodecahedron, with carbon atoms at each vertex.
Role-Playing Games
In tabletop role-playing games like Dungeons & Dragons, 12-sided dice (dodecahedrons) are used to generate random numbers between 1 and 12.
Coins Around the World
Several countries have issued 12-sided coins, including the British One Pound coin, Australian 50-cent coin, and the Cook Islands 5-dollar coin.




