Equation of a Line - Definition, Examples, Quiz, FAQ, Trivia
Learn about different forms of linear equations with easy explanations and practice activities
What is a Linear Equation?
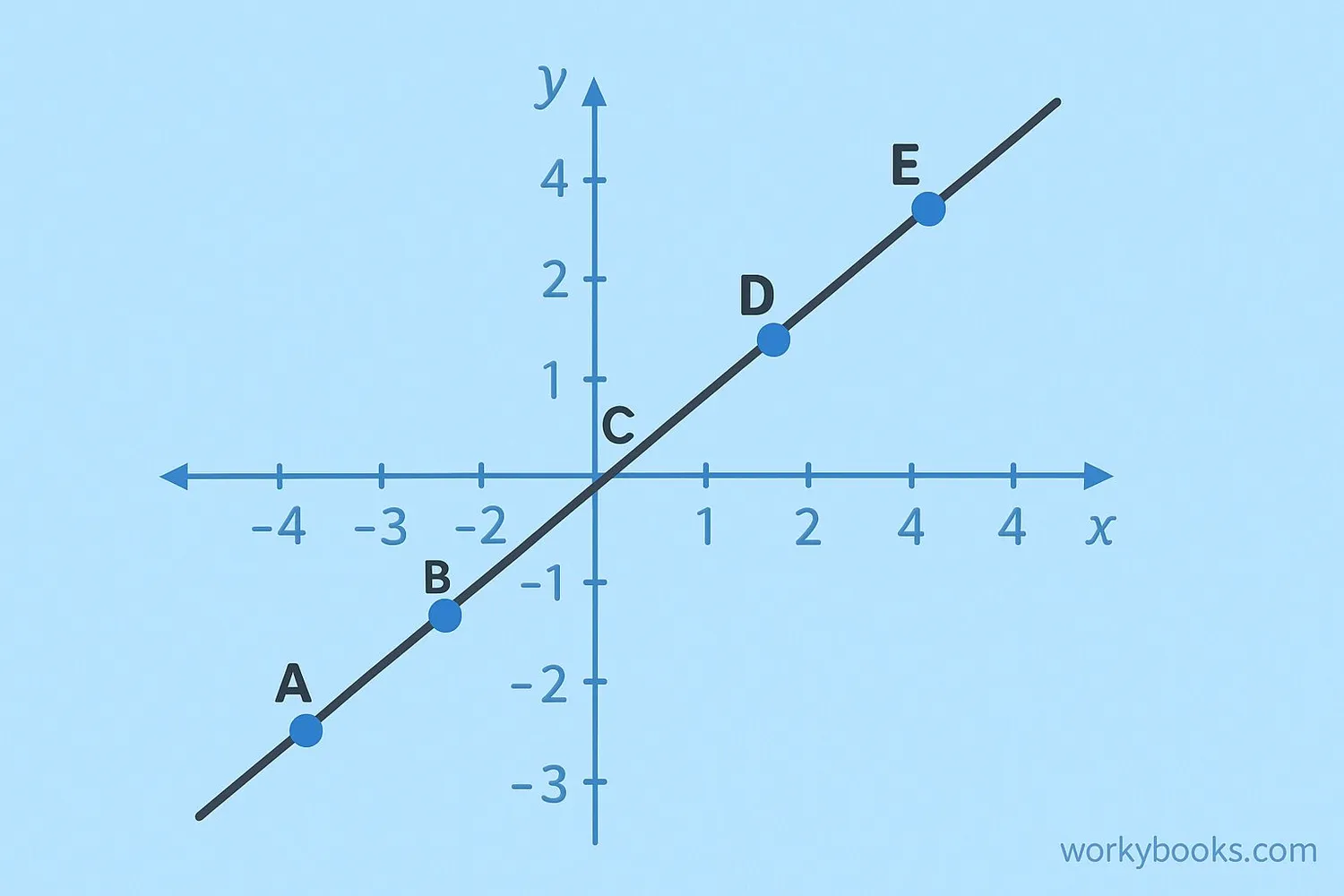
A linear equation is a mathematical statement that shows the relationship between two variables (usually x and y) that creates a straight line when graphed on a coordinate plane.
Linear equations are powerful tools that help us describe relationships between quantities. For example, they can show how the cost of apples relates to how many pounds you buy, or how the temperature changes over time.
All linear equations follow this general pattern: y = mx + b, where m represents the slope (steepness) of the line and b represents the y-intercept (where the line crosses the y-axis).
Key Concept
A linear equation always graphs to a straight line and has variables that are only to the first power (no x² or y³ terms).
Slope-Intercept Form
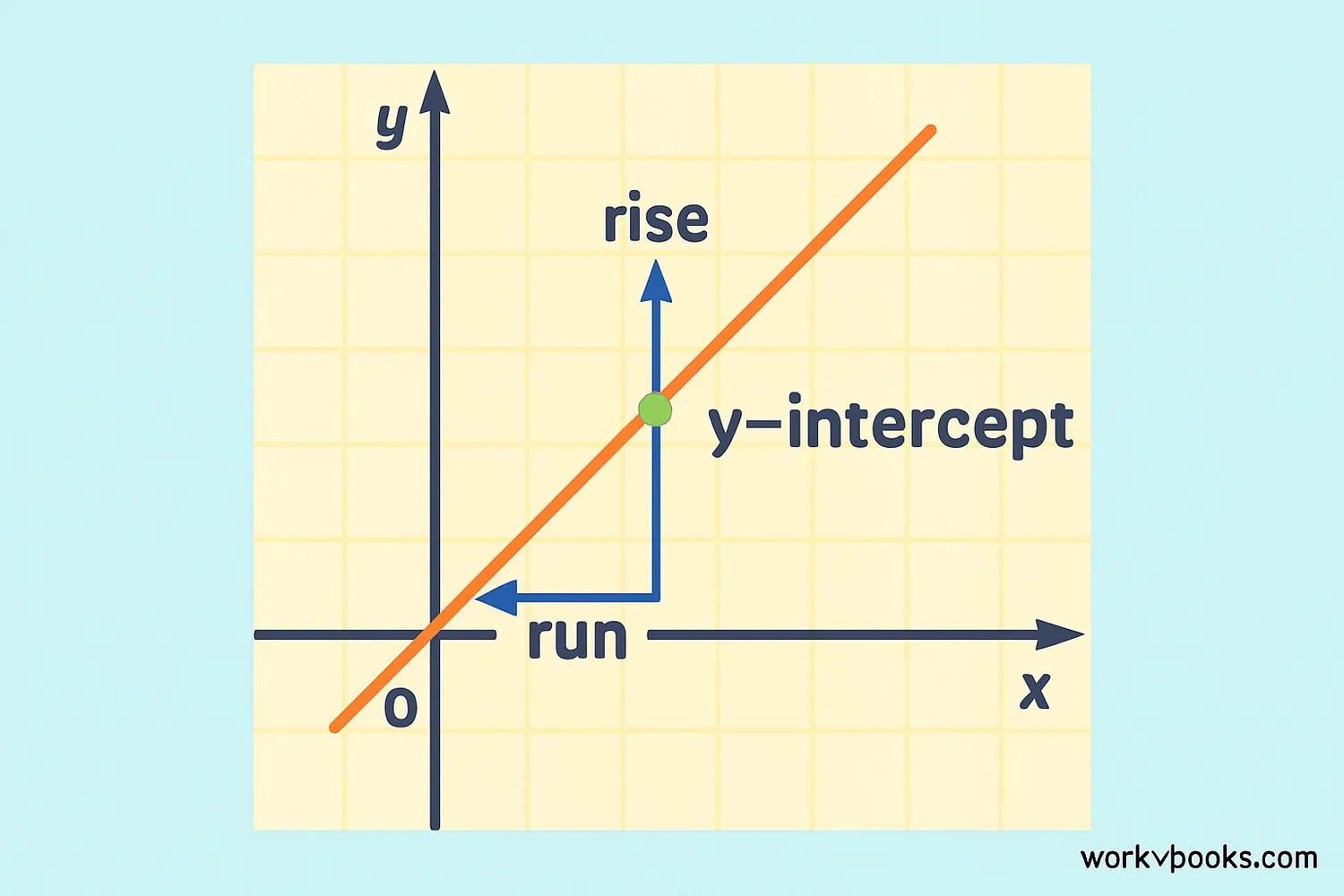
The slope-intercept form is the most common way to write a linear equation. It looks like this:
Slope-Intercept Formula
Where m is the slope and b is the y-intercept
Slope (m): This tells us how steep the line is. It's calculated as "rise over run" - how much the line goes up or down divided by how much it goes left or right.
Y-intercept (b): This is the point where the line crosses the y-axis. It tells us the value of y when x is zero.
Example: In the equation y = 2x + 3, the slope is 2 and the y-intercept is 3. This means the line crosses the y-axis at (0, 3) and for every 1 unit you move right, you move 2 units up.
Remember
Positive slope means the line goes upward from left to right. Negative slope means it goes downward.
Point-Slope Form
Sometimes we know one point on the line and the slope, but not the y-intercept. In these cases, we use the point-slope form:
Point-Slope Formula
Where m is the slope and (x₁, y₁) is a point on the line
Example: If we know a line has slope 4 and passes through the point (1, 2), we can write the equation as: y - 2 = 4(x - 1)
We can then simplify this to slope-intercept form: y - 2 = 4x - 4 → y = 4x - 2
Conversion Tip
You can always convert from point-slope form to slope-intercept form by solving for y.
General Form of a Line
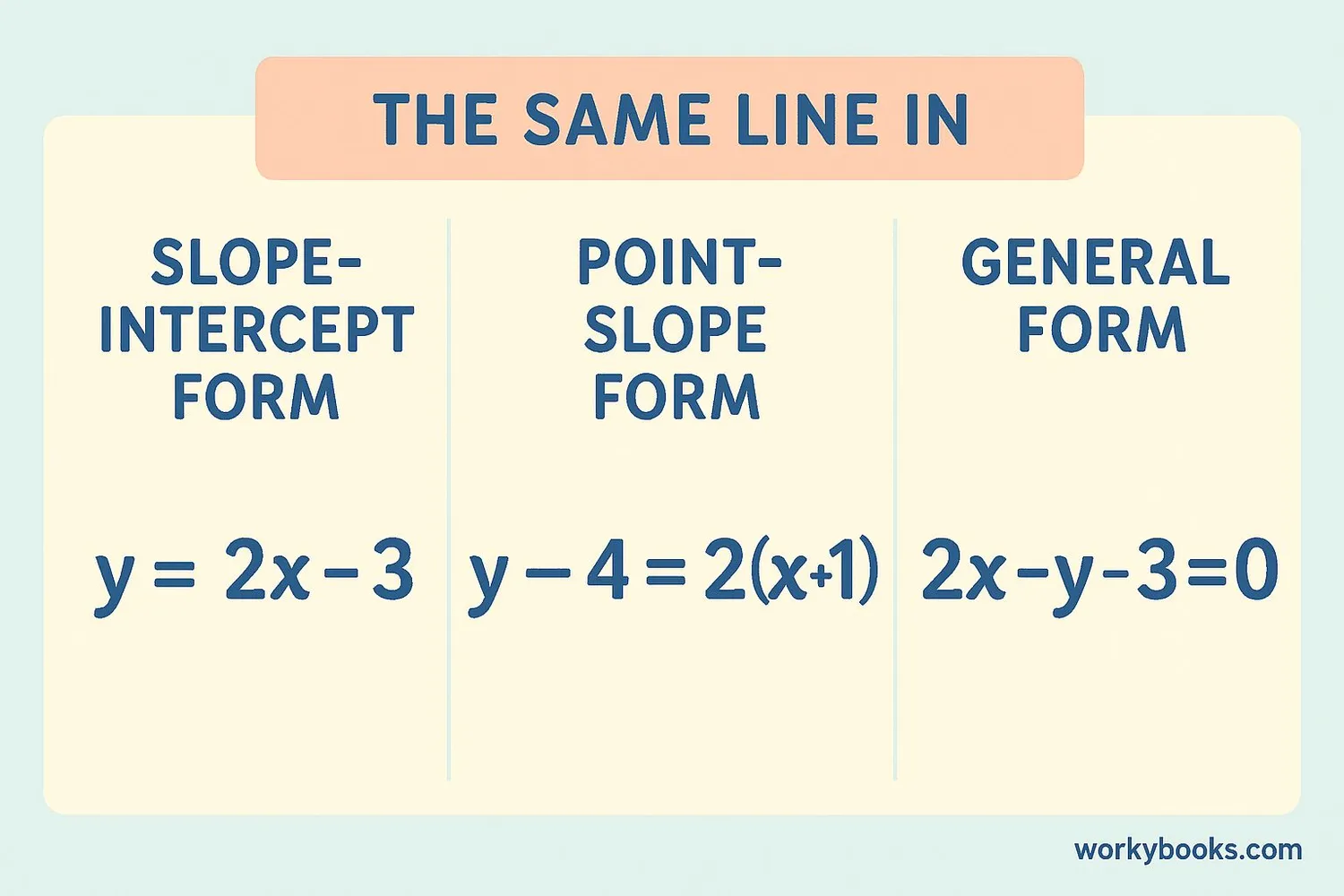
The general form of a linear equation is another way to write linear equations. It looks like this:
General Form
Where A, B, and C are integers, and A should be positive
Example: The equation y = 2x + 3 can be rewritten in general form as: 2x - y = -3
To convert from slope-intercept form to general form:
1. Move all terms to one side: y = 2x + 3 → 2x - y + 3 = 0
2. If necessary, multiply through to eliminate fractions: 2x - y = -3
The general form is useful for certain calculations and for comparing equations.
Remember
In general form, we usually want A to be positive and all coefficients to be integers with no common factors.
X and Y Intercepts
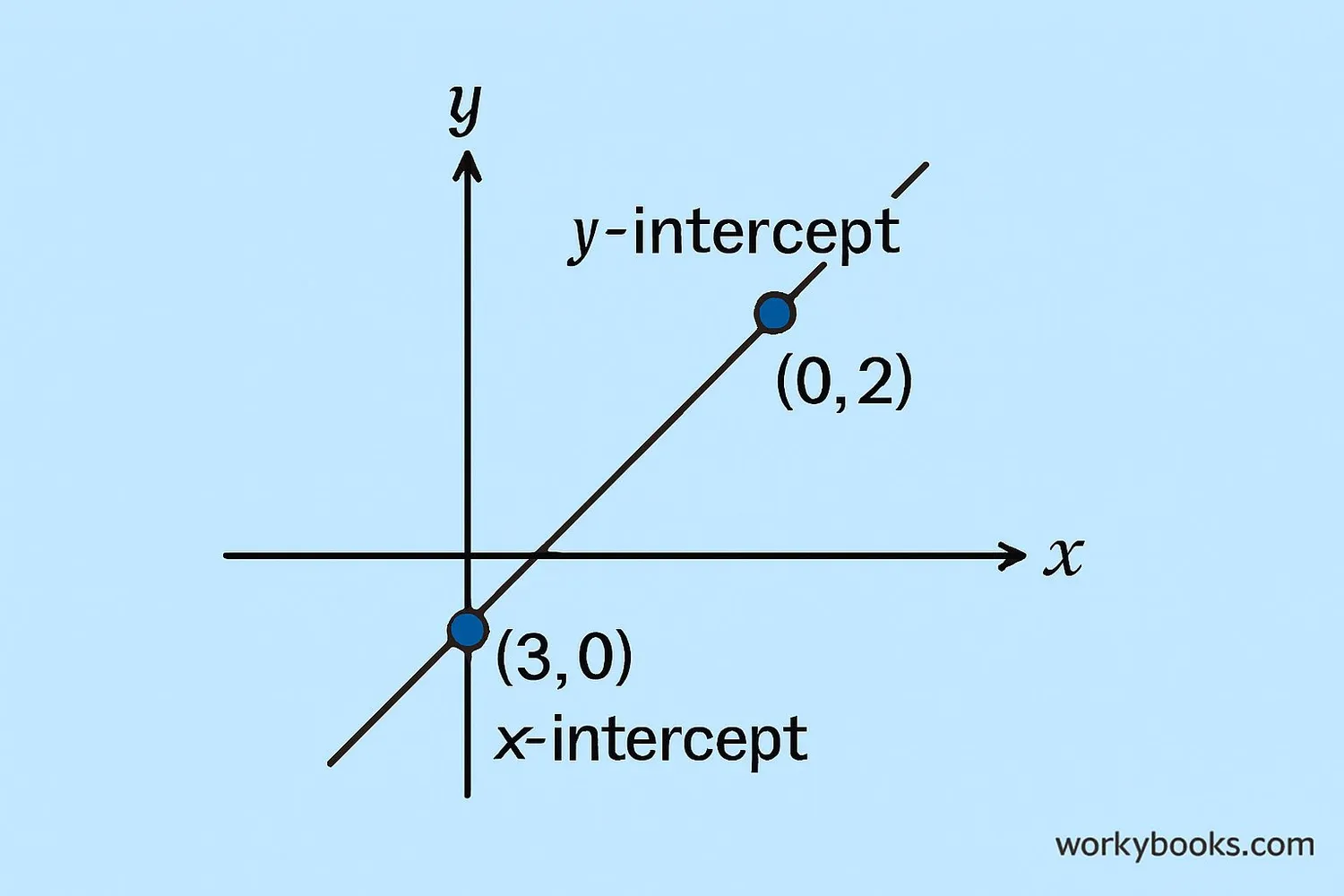
Intercepts are important points where a line crosses the axes. There are two types:
Y-intercept: This is where the line crosses the y-axis. At this point, x = 0. In the slope-intercept form y = mx + b, the y-intercept is b.
X-intercept: This is where the line crosses the x-axis. At this point, y = 0. To find the x-intercept, set y = 0 in the equation and solve for x.
Example: For the equation y = 2x + 6:
Y-intercept: When x = 0, y = 2(0) + 6 = 6 → (0, 6)
X-intercept: When y = 0, 0 = 2x + 6 → 2x = -6 → x = -3 → (-3, 0)
Intercepts are helpful for graphing lines quickly. If you know both intercepts, you can plot them and draw the line through them.
Graphing Tip
To graph a line quickly, find both intercepts, plot them, and draw a line through them.
Equation of a Line Quiz
Test your understanding of linear equations with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about linear equations:
Math Trivia
Discover interesting facts about linear equations and mathematics:
Ancient Equations
The concept of linear equations dates back to ancient Egyptian and Babylonian mathematics around 1800 BC. They used these equations to solve practical problems like distributing goods and calculating land areas.
Real-World Applications
Linear equations are used in countless real-world situations including predicting profits in business, calculating dosages in medicine, determining speed in physics, and even in video game programming.
Space Exploration
NASA engineers use linear equations to calculate rocket trajectories, plan orbital paths, and determine fuel requirements. The Mars rovers' paths are planned using systems of linear equations.
Graphing Record
The longest straight line ever drawn was 107.7 miles long, created in the desert of Oman in 2019. If graphed, this would create a linear equation with a slope of zero!


