Straight Line - Definition, Examples, Quiz, FAQ, Trivia
Learn about linear equations, different forms, graphing lines, and solving problems
What is a Linear Equation?
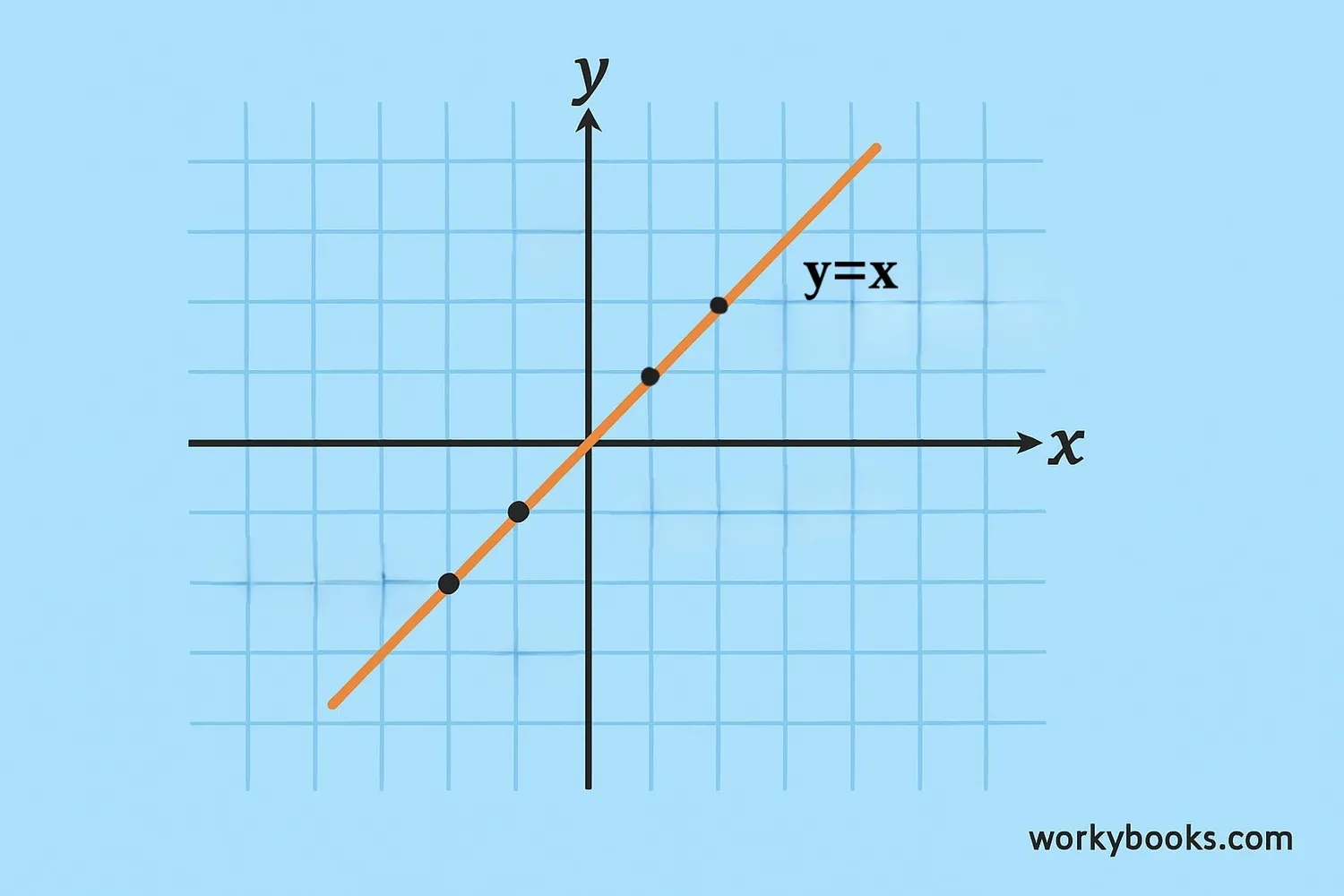
A linear equation is an equation that creates a straight line when graphed on a coordinate plane. It shows the relationship between two variables, usually x and y.
The general form of a linear equation is: Ax + By = C, where A, B, and C are numbers.
Linear equations are used to model real-world situations where there is a constant rate of change. For example, if you earn $10 per hour, your earnings can be represented by the equation y = 10x, where x is hours worked and y is money earned.
Key Concept
All linear equations graph as straight lines. The steepness and position of the line depend on the numbers in the equation.
Slope-Intercept Form
The slope-intercept form is the most common way to write a linear equation. It looks like this:
Slope-Intercept Form
Where m is the slope and b is the y-intercept
Y-intercept (b): The point where the line crosses the y-axis. This happens when x = 0.
Let's look at an example: y = 2x + 3
The slope (m) is 2, which means the line rises 2 units for every 1 unit it moves right.
The y-intercept (b) is 3, so the line crosses the y-axis at point (0, 3).
Remember
Positive slope means the line goes upward from left to right. Negative slope means it goes downward.
Point-Slope Form
The point-slope form is useful when you know one point on the line and the slope. The formula is:
Point-Slope Form
Where m is the slope and (x₁, y₁) is a point on the line
Example: Write the equation of a line with slope 3 that passes through point (2, 5)
Step 1: Identify m, x₁, and y₁ → m = 3, x₁ = 2, y₁ = 5
Step 2: Plug into the formula → y - 5 = 3(x - 2)
Step 3: Simplify if needed → y - 5 = 3x - 6 → y = 3x - 1
So the equation of the line is y = 3x - 1.
Conversion Tip
You can convert between different forms of linear equations by simplifying and rearranging the terms.
Graphing Lines
Graphing a linear equation helps us visualize the relationship between variables. Here's how to graph a line from the slope-intercept form (y = mx + b):
Step 1: Plot the y-intercept (b) on the y-axis.
Step 2: Use the slope (m) to find another point. Remember, slope = rise/run.
Step 3: Draw a line through the two points, extending it in both directions.
Let's practice with an example: Graph y = 2x + 1
Step 1: The y-intercept is 1, so plot point (0, 1)
Step 2: The slope is 2 (which is 2/1), so from (0, 1), go up 2 units and right 1 unit to point (1, 3)
Step 3: Draw a line through (0, 1) and (1, 3)
You've now graphed the line! You can find more points to check your work.
Graphing Tip
Always find at least two points to draw your line. A third point can help verify your line is correct.
Real-World Examples
Linear equations are used in many real-world situations. Let's look at some examples:
Example 1: Taxi Fare
A taxi charges $3.50 plus $2.25 per mile. The equation is: y = 2.25x + 3.50, where x is miles and y is total cost.
Example 2: Phone Plan
A phone plan costs $20 per month plus $0.10 per text message. The equation is: y = 0.10x + 20, where x is texts and y is monthly cost.
Example 3: Baking Cookies
A recipe calls for 2 cups of flour plus 1.5 cups per batch. The equation is: y = 1.5x + 2, where x is batches and y is total flour.
Example 4: Temperature Conversion
To convert Celsius to Fahrenheit: F = 1.8C + 32. This is a linear equation!
Can you think of other examples from your daily life?
Application Tip
Look for situations with a constant rate of change (slope) and a starting value (y-intercept) to identify linear relationships.
Linear Equations Practice Quiz
Test your understanding of linear equations with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about linear equations:
Math Trivia
Discover interesting facts about linear equations and mathematics:
Ancient Origins
The concept of linear equations dates back to ancient Egyptian and Babylonian mathematics around 1800 BC. The Rhind Mathematical Papyrus from ancient Egypt contains problems that we would now solve using linear equations.
Real-World Applications
Linear equations are used in countless real-world applications including economics (supply and demand curves), physics (motion at constant speed), engineering (structural analysis), and even video game design (character movement).
Space Exploration
NASA uses linear equations in rocket trajectory calculations. The path of a rocket during certain phases of flight can be approximated using linear equations, helping scientists plan missions to other planets.
Mathematical Foundation
Linear algebra, which extends the concept of linear equations to multiple dimensions, is considered one of the most important areas of mathematics. It's essential for computer graphics, artificial intelligence, and quantum mechanics.


