Exponents - Definition, Examples, Quiz, FAQ, Trivia
Learn about powers, exponential notation, and exponent rules with simple explanations and practice activities
What are Exponents?

Exponents are a special way to show repeated multiplication. Instead of writing 2 × 2 × 2 × 2, we can write 24. The small number (4) is called the exponent or power, and the big number (2) is called the base.
In the expression 53:
- 5 is the base (the number being multiplied)
- 3 is the exponent (how many times to multiply the base)
- 53 = 5 × 5 × 5 = 125
Exponents help us write very large numbers and very small numbers in a simpler way. For example, 106 is much easier to write than 1,000,000!
= 3 × 3 × 3 × 3 = 81
Key Concept
The exponent tells us how many times to multiply the base by itself. 23 means 2 × 2 × 2, not 2 × 3!
Laws of Exponents
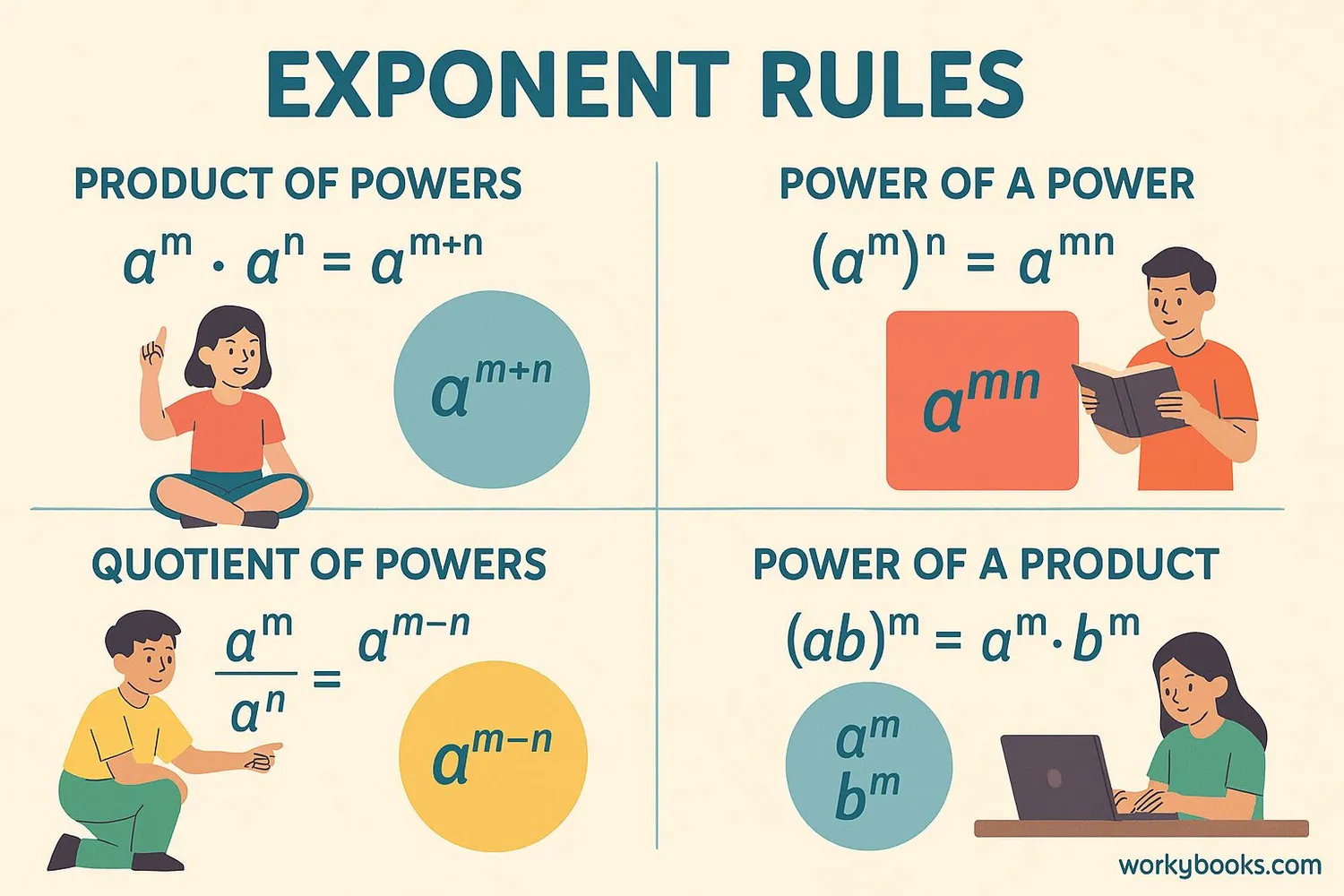
There are special rules that make working with exponents easier. These laws help us simplify expressions with exponents:
Product Rule
When multiplying powers with the same base, add the exponents.
Example: 23 × 24 = 23+4 = 27 = 128
Quotient Rule
When dividing powers with the same base, subtract the exponents.
Example: 56 ÷ 52 = 56-2 = 54 = 625
Power of a Power
When raising a power to another power, multiply the exponents.
Example: (32)3 = 32×3 = 36 = 729
Zero Exponent Rule
Any base (except zero) raised to the power of zero equals 1.
Example: 70 = 1
Negative Exponent Rule
A negative exponent means to take the reciprocal of the base and make the exponent positive.
Example: 4-2 = 1/42 = 1/16
Fractional Exponent
A fractional exponent represents a root.
Example: 81/3 = ∛8 = 2
Remember
These rules only work when the bases are the same! You can't combine exponents with different bases using these rules.
Exponent Examples
Example 1: Simple Calculation
Problem: Simplify 24
Solution: 24 = 2 × 2 × 2 × 2 = 16
Example 2: Product Rule
Problem: Simplify 32 × 35
Solution: 32+5 = 37 = 2187
Example 3: Quotient Rule
Problem: Simplify 108 ÷ 103
Solution: 108-3 = 105 = 100,000
Example 4: Power of Power
Problem: Simplify (52)3
Solution: 52×3 = 56 = 15,625
Example 5: Zero Exponent
Problem: Simplify 90
Solution: Any number (except 0) to the power of 0 is 1. Answer: 1
Example 6: Negative Exponent
Problem: Simplify 4-2
Solution: 4-2 = 1/42 = 1/16
Practice Tip
Start with small numbers when practicing exponents. Try calculating 2n for n from 0 to 10 - you'll see a pattern!
Exponent Practice Quiz
Test your understanding of exponents with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about exponents:
Math Trivia
Discover interesting facts about exponents and powers:
Ancient Exponents
The concept of exponents dates back to ancient Egypt around 2000 BC. Egyptian mathematicians used a form of exponential notation in their calculations, particularly for area and volume measurements.
Really Big Numbers
A googol is 10100 (1 followed by 100 zeros). Google's name is a play on this term. But there's an even bigger number called a googolplex, which is 10googol!
Paper Folding Challenge
If you could fold a piece of paper in half 42 times, it would reach the moon! This demonstrates exponential growth - each fold doubles the thickness: 242 is about 439,804 kilometers.
Computer Exponents
Computers use exponents in binary (base-2) system. A kilobyte is 210 = 1024 bytes, a megabyte is 220 = 1,048,576 bytes, and a gigabyte is 230 = 1,073,741,824 bytes!





