Exterior Angle Theorem - Definition, Examples, Quiz, FAQ, Trivia
Learn about triangle angles with easy explanations and practice activities
What is the Exterior Angle Theorem?
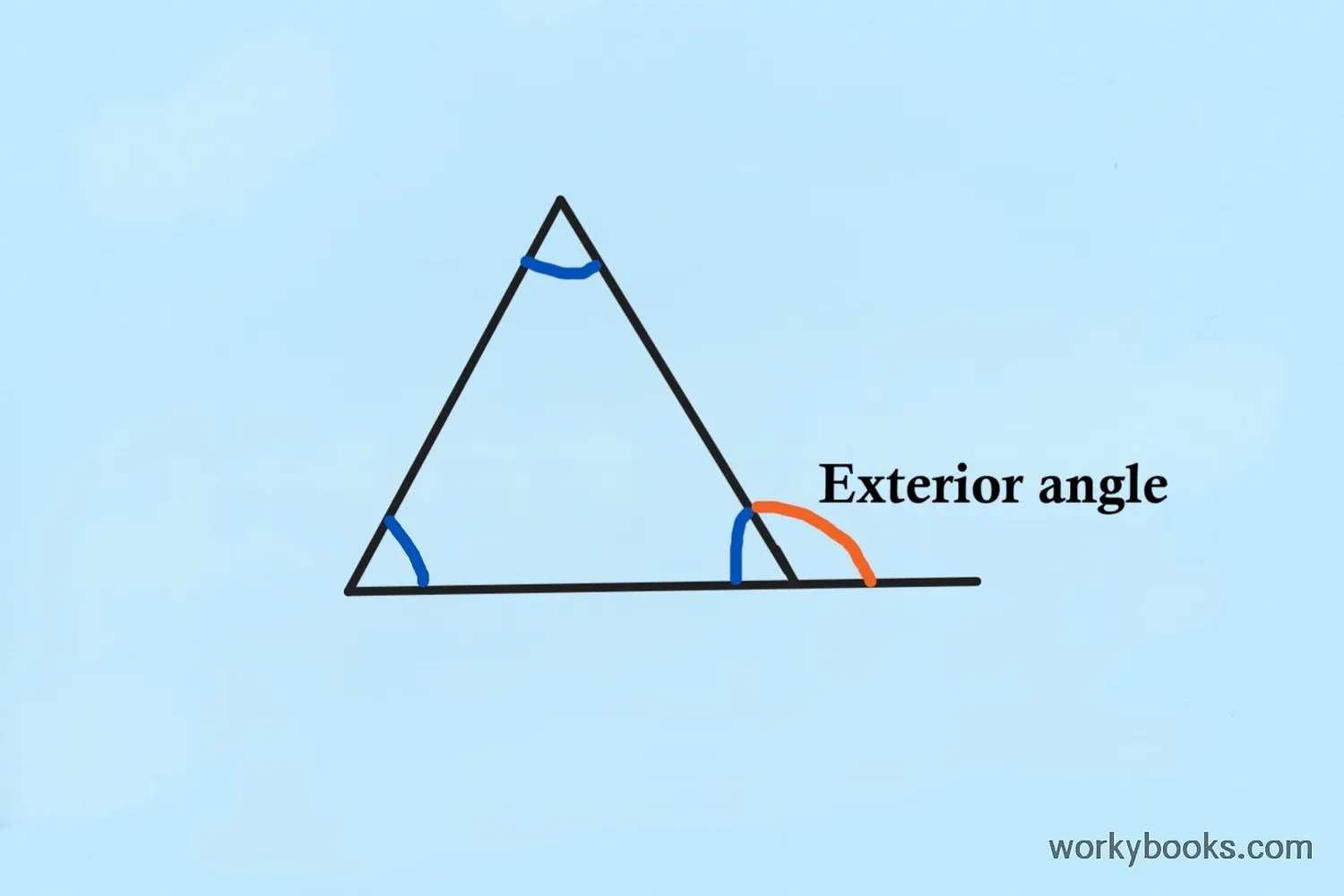
The Exterior Angle Theorem is an important rule in geometry that helps us understand the relationship between the angles inside and outside a triangle.
An exterior angle is formed when one side of a triangle is extended outward. This creates an angle outside the triangle that sits next to one of the interior angles.
The theorem tells us that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles. These are the two angles inside the triangle that are not adjacent to the exterior angle.
Understanding this theorem helps us solve many geometry problems involving triangles and their angles.
Key Concept
Exterior Angle = Sum of Two Remote Interior Angles. This relationship helps us find missing angle measurements in triangles.
Understanding Exterior and Interior Angles
To understand the Exterior Angle Theorem, we first need to know about different types of angles in a triangle:
Interior Angles: These are the three angles inside the triangle. The sum of all interior angles in any triangle is always 180 degrees.
Exterior Angle: This is formed when we extend one side of the triangle. Each triangle has three possible exterior angles, one at each vertex.
Adjacent Interior Angle: This is the interior angle that is right next to the exterior angle. Together, they form a straight line (180 degrees).
Remote Interior Angles: These are the two interior angles that are not adjacent to the exterior angle. They are "remote" because they are farther away from the exterior angle.
Angle Relationships
The exterior angle equals the sum of the two non-adjacent interior angles.
The Exterior Angle Theorem Explained
Let's break down why the Exterior Angle Theorem works:
Step 1: We know that the sum of all three interior angles in a triangle is always 180°.
Step 2: We also know that an exterior angle and its adjacent interior angle form a straight line, which measures 180°.
Step 3: This means the exterior angle equals 180° minus the adjacent interior angle.
Step 4: But the sum of the two remote interior angles also equals 180° minus the adjacent interior angle (because all three interior angles add to 180°).
Step 5: Therefore, the exterior angle must equal the sum of the two remote interior angles.
Remember
Each exterior angle of a triangle equals the sum of the two interior angles that are not next to it. This is true for all three exterior angles.
Examples of the Exterior Angle Theorem
Let's see how the Exterior Angle Theorem works with some examples:
Example 1: In a triangle, the two remote interior angles measure 40° and 60°. What is the measure of the exterior angle?
Solution: Exterior angle = 40° + 60° = 100°
Example 2: An exterior angle of a triangle measures 120°. If one remote interior angle measures 50°, what is the measure of the other remote interior angle?
Solution: Other remote interior angle = 120° - 50° = 70°
Example 3: In triangle ABC, angle A = 30° and angle B = 40°. What is the measure of the exterior angle at vertex C?
Solution: Exterior angle at C = angle A + angle B = 30° + 40° = 70°
Example 4: The exterior angle at vertex A of a triangle measures 110°. If the remote interior angles are equal, what is the measure of each?
Solution: Each remote interior angle = 110° ÷ 2 = 55°
Practice Tip
When solving problems, always identify which angles are the remote interior angles relative to the exterior angle you're working with.
Practice Quiz
Test your understanding of the Exterior Angle Theorem with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the Exterior Angle Theorem:
Geometry Trivia
Discover interesting facts about triangles and geometry:
Ancient Geometry
The study of triangles dates back to ancient civilizations. The Egyptians used triangles in the construction of pyramids as early as 2700 BCE, applying geometric principles without formal theorems.
Strong Shapes
Triangles are the strongest geometric shape because their fixed angles distribute force evenly. This is why you see triangles in bridges, towers, and other structures that need to be strong and stable.
Triangles in Space
NASA engineers use triangular shapes in spacecraft design because of their strength and stability. The Exterior Angle Theorem helps in calculating precise angles for various components.
Largest Triangle
The largest man-made triangle is the Bermuda Triangle, covering about 500,000 square miles of ocean. However, the "triangle" in nature that most interests mathematicians is the Great Triangle on the celestial sphere used in astronomy.





