Factor Tree Method - Definition, Examples, Quiz, FAQ, Trivia
Learn to break down numbers into prime factors with visual diagrams and practice activities
What is a Factor Tree?
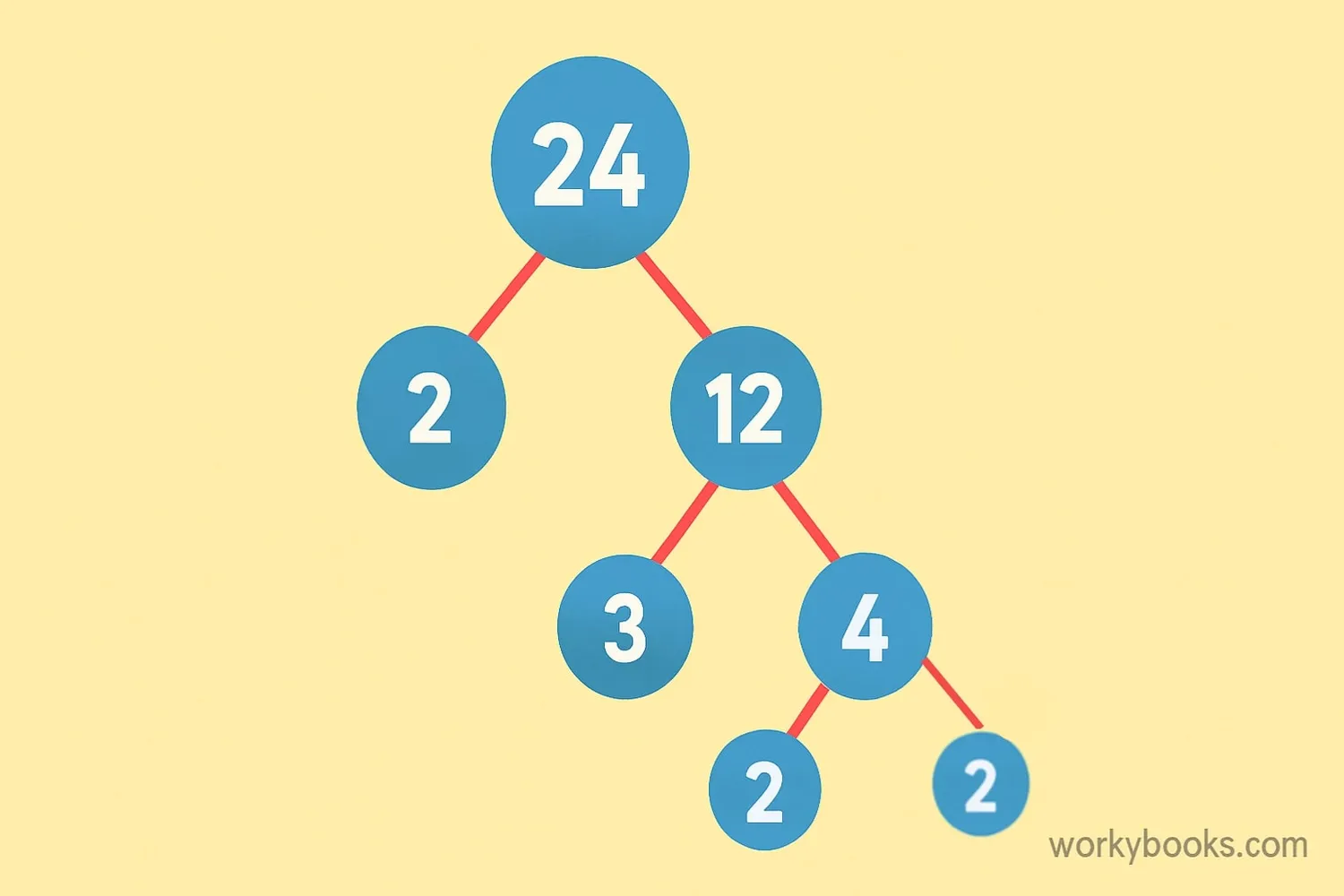
A factor tree is a diagram that helps us break down a number into its prime factors. We start with the original number at the top, then draw branches to show which numbers multiply together to make it. We continue breaking down the numbers until we're left with only prime numbers at the bottom.
Factor trees help us understand how numbers are built from smaller numbers, just like a real tree has branches that get smaller as they extend from the trunk. This method is especially useful for finding the prime factorization of a number, which means writing it as a product of prime numbers.
The prime factorization is like a number's DNA—it shows the unique combination of prime numbers that multiply together to create the original number.
Key Concept
Every composite number can be expressed as a product of prime factors. This is called the Fundamental Theorem of Arithmetic.
Prime and Composite Numbers

Before we can understand factor trees, we need to know about two important types of numbers:
Prime numbers are numbers greater than 1 that have exactly two factors: 1 and themselves. Examples include 2, 3, 5, 7, 11, and 13. Prime numbers are like the atoms of mathematics—they can't be broken down into smaller whole number factors.
Composite numbers are numbers that have more than two factors. These numbers can be broken down into smaller factors. Examples include 4, 6, 8, 9, 10, and 12. All composite numbers can be written as products of prime numbers.
The number 1 is special—it's neither prime nor composite. It's called a unit.
Remember
2 is the only even prime number. All other even numbers are composite because they can be divided by 2.
How to Make a Factor Tree

Creating a factor tree is like solving a puzzle. Let's break it down into simple steps:
Steps to Create a Factor Tree
There's often more than one way to build a factor tree, but you'll always end up with the same prime factors. For example, you could start with different factor pairs, but the final prime factorization will be identical.
Pro Tip
Start with the smallest prime factor whenever possible to create the most organized factor tree.
GCF and LCM with Factor Trees
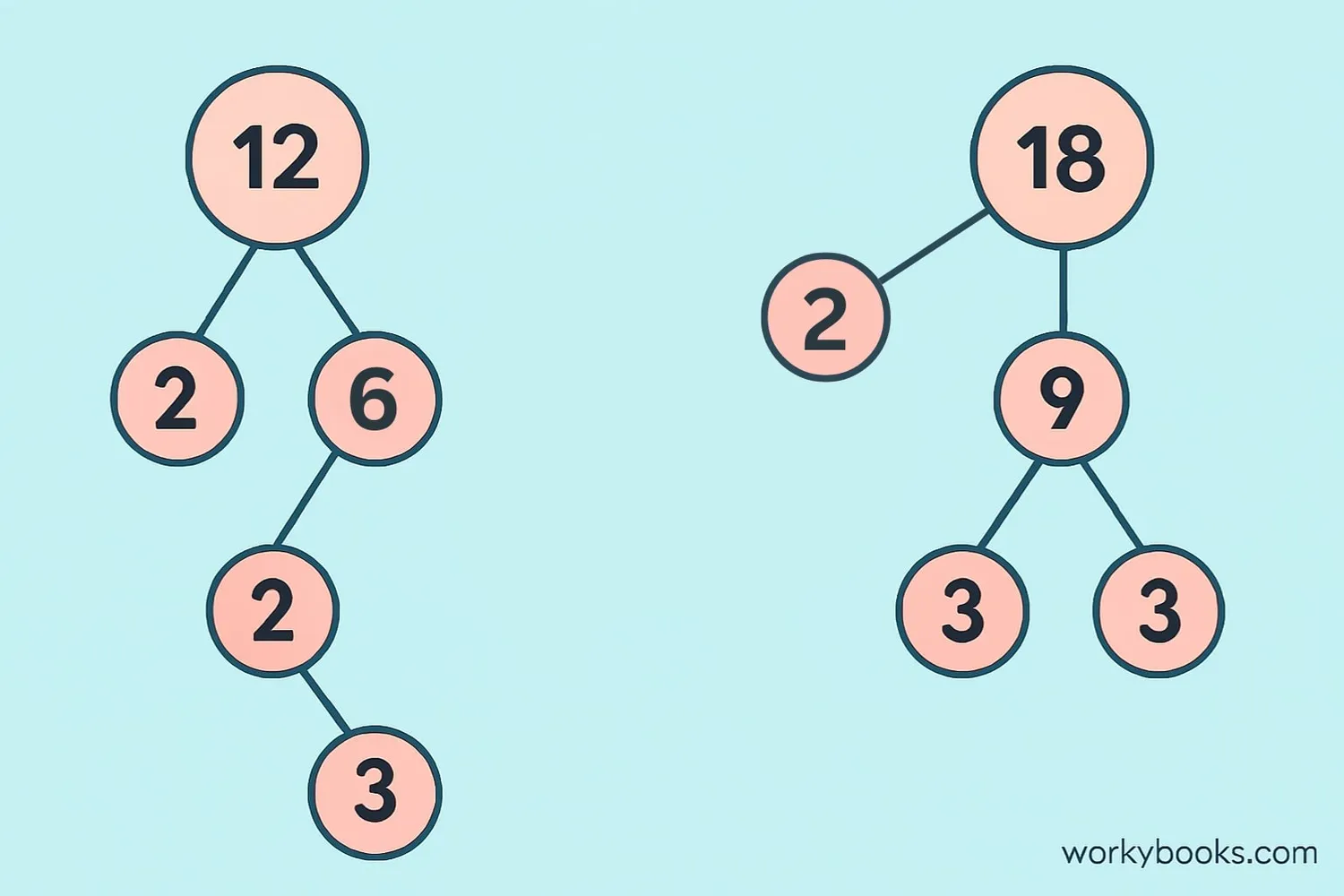
Factor trees are especially helpful for finding the Greatest Common Factor (GCF) and Least Common Multiple (LCM) of two or more numbers.
The GCF is the largest number that divides evenly into two or more numbers. To find it using factor trees:
- Create factor trees for each number
- Identify the common prime factors
- Multiply these common factors together
The LCM is the smallest number that is a multiple of two or more numbers. To find it using factor trees:
- Create factor trees for each number
- Take all the prime factors from each number
- Use the highest power of each prime that appears
- Multiply these together
Example: GCF and LCM of 12 and 18
12 = 2 × 2 × 3 = 2² × 3
18 = 2 × 3 × 3 = 2 × 3²
GCF = common factors = 2 × 3 = 6
LCM = all factors (highest power) = 2² × 3² = 4 × 9 = 36
Remember
For any two numbers, GCF × LCM = Product of the two numbers. For 12 and 18: 6 × 36 = 216, and 12 × 18 = 216.
Factor Tree Examples
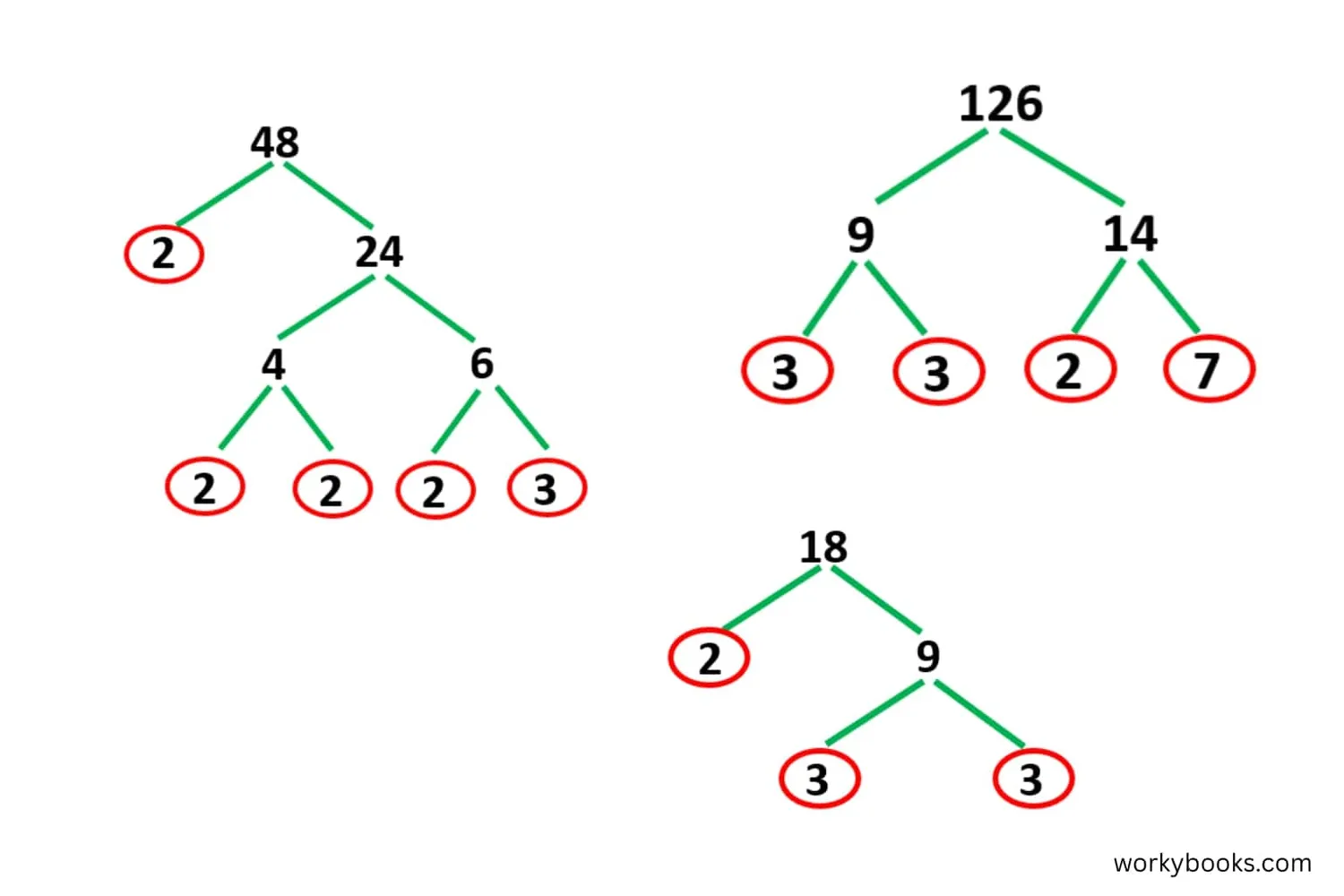
Let's look at some examples to see factor trees in action:
Example 1: Factor Tree for 48
Prime factorization: 2 × 2 × 2 × 2 × 3 = 2⁴ × 3
Example 2: Factor Tree for 60
Prime factorization: 2 × 2 × 3 × 5 = 2² × 3 × 5
Example 3: Factor Tree for 100
Prime factorization: 2 × 2 × 5 × 5 = 2² × 5²
Practice Tip
Try creating factor trees for numbers you encounter in daily life, like your age, the number of students in your class, or pages in your book.
Factor Tree Practice Quiz
Test your understanding of factor trees with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about factor trees:
Math Trivia
Discover interesting facts about numbers and factorization:
Ancient Factorization
The ancient Greeks were among the first to study prime numbers over 2,000 years ago. Euclid proved that there are infinitely many prime numbers around 300 BCE.
Prime Numbers in Nature
Some insects like cicadas use prime numbers in their life cycles. The North American cicada emerges every 13 or 17 years—both prime numbers—which helps avoid synchronization with predators.
Prime Numbers and Security
Prime factorization is used in cryptography to secure online communications. It's easy to multiply two large primes together, but very difficult to factor the result back into the original primes.
Largest Known Prime
The largest known prime number (as of 2023) is 2⁸²⁵⁸⁹⁹³³ − 1, a number with 24,862,048 digits! It was found by Patrick Laroche as part of the Great Internet Mersenne Prime Search.





