Fraction to Decimal - Definition, Examples, Quiz, FAQ, Trivia
Learn to convert between fractions and decimals with easy explanations and practice activities
What is Fraction to Decimal Conversion?

Converting a fraction to a decimal means changing it from a fraction form (like 12) to a decimal form (like 0.5). This is useful because decimals are often easier to work with in calculations and measurements.
Every fraction represents a division problem: the numerator divided by the denominator. For example, 34 means 3 divided by 4, which equals 0.75.
Why do we need to convert? Decimals are commonly used in money, measurements, and calculators. Being able to switch between fractions and decimals helps us understand math in different ways.
Key Concept
A fraction is just division: numerator ÷ denominator = decimal. This relationship is the foundation for all fraction-to-decimal conversions.
How to Convert Fractions to Decimals
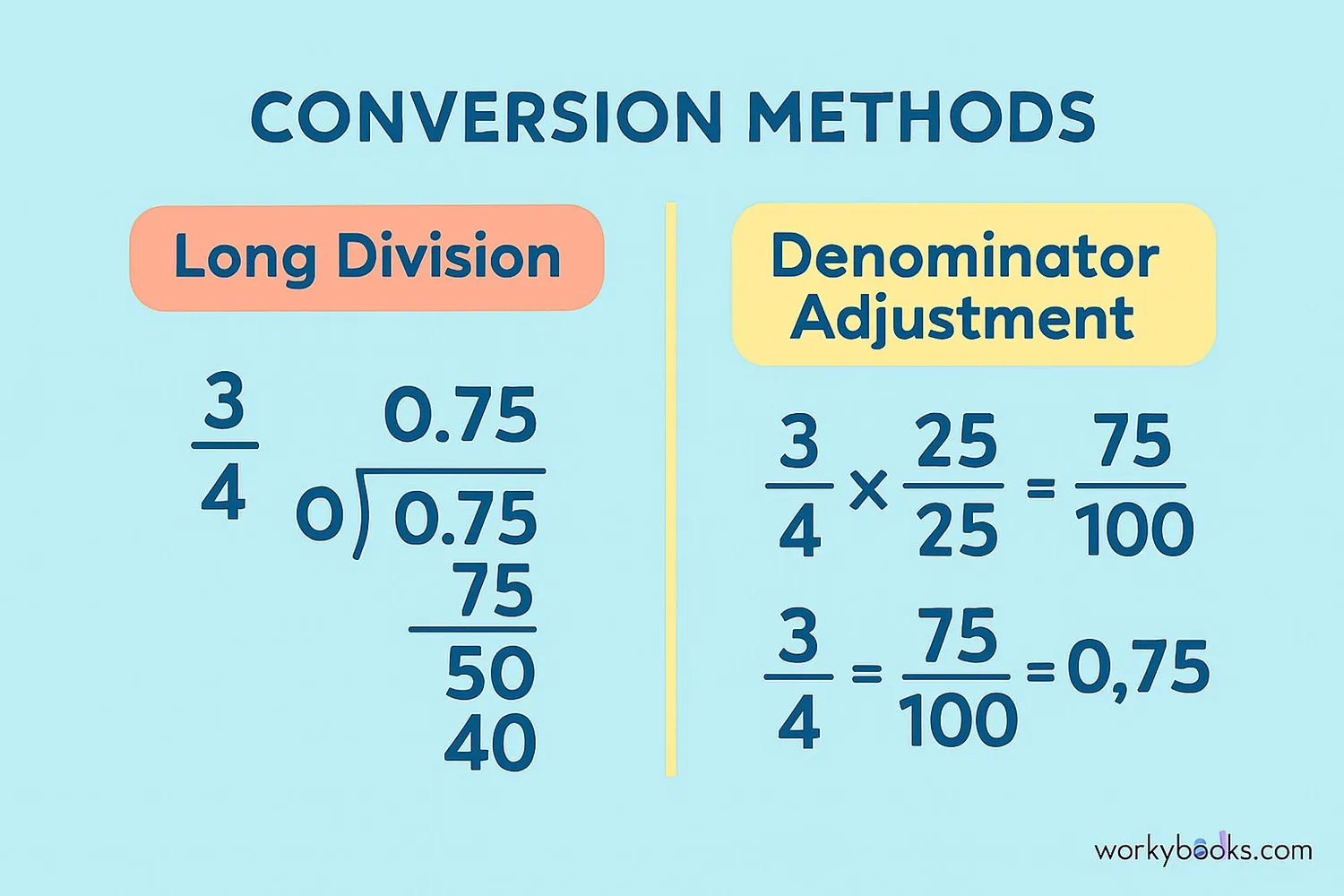
There are two main ways to convert fractions to decimals. Let's look at both methods:
Method 1: Long Division
Divide the numerator by the denominator. This works for any fraction.
Example: Convert 38 to a decimal
Step 1: Divide 3 by 8 → 3 ÷ 8
Step 2: 8 goes into 3.0 how many times? 0.375
Step 3: So 38 = 0.375
Method 2: Denominator Adjustment
Make the denominator 10, 100, 1000, etc. by multiplying both numerator and denominator by the same number.
Example: Convert 14 to a decimal
Step 1: Multiply numerator and denominator by 25: 1 × 254 × 25 = 25100
Step 2: 25100 = 0.25
Conversion Formula
To convert any fraction to a decimal, divide the numerator by the denominator.
Remember
Some fractions convert to repeating decimals. For example, 13 = 0.333... with the 3 repeating forever.
Fraction to Decimal Conversion Charts

Conversion charts help us quickly find decimal equivalents for common fractions. Here are two useful charts:
Common Fraction to Decimal Chart
| Fraction | Decimal |
|---|---|
| 1/2 | 0.5 |
| 1/3 | 0.333... |
| 2/3 | 0.666... |
| 1/4 | 0.25 |
| 3/4 | 0.75 |
| 1/5 | 0.2 |
| 2/5 | 0.4 |
| 3/5 | 0.6 |
| 4/5 | 0.8 |
| 1/8 | 0.125 |
| 3/8 | 0.375 |
| 5/8 | 0.625 |
| 7/8 | 0.875 |
| 1/10 | 0.1 |
| 1/100 | 0.01 |
Equivalent Fractions and Decimals
| Fraction | Decimal | Percentage |
|---|---|---|
| 1/1 | 1.0 | 100% |
| 1/2 | 0.5 | 50% |
| 1/4 | 0.25 | 25% |
| 3/4 | 0.75 | 75% |
| 1/5 | 0.2 | 20% |
| 1/10 | 0.1 | 10% |
| 1/100 | 0.01 | 1% |
Chart Tip
Notice how fractions with denominators that are factors of 10 (like 2, 4, 5, 10) have exact decimal equivalents? These are the easiest to convert!
Real-World Examples

Let's practice conversion with some real-world examples:
Example 1: A pizza is cut into 8 slices. You eat 3 slices. What fraction did you eat? What is this as a decimal?
Solution: 38 = 0.375
Example 2: You have $0.75. What fraction of a dollar is this?
Solution: $0.75 = 75100 = 34
Example 3: A recipe calls for 0.5 cups of sugar. What fraction of a cup is this?
Solution: 0.5 = 12
Example 4: Convert 25 to a decimal using both methods.
Long Division: 2 ÷ 5 = 0.4
Denominator Adjustment: 2 × 25 × 2 = 410 = 0.4
Practice converting fractions you see in recipes, measurements, and money!
Conversion Tip
To convert a decimal back to a fraction, write the decimal as the numerator and 1 as the denominator, then multiply numerator and denominator by 10 for each digit after the decimal point.
Conversion Practice Quiz
Test your conversion skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about fraction to decimal conversion:
Math Trivia
Discover interesting facts about fractions and decimals:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They mostly used unit fractions (fractions with numerator 1) and represented them with hieroglyphs.
Decimal Point Origin
The decimal point was introduced by John Napier in the early 17th century. Before that, mathematicians used various symbols or wrote decimals as fractions.
Calculator Precision
Most calculators can display only 8-10 decimal places, but mathematical constants like π have been calculated to over 50 trillion decimal places!
Golden Ratio
The golden ratio (approximately 1.618) is a special decimal that appears in nature, art, and architecture. It can be expressed as (1 + √5)/2.





