Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn about parts of a whole with visual models, fraction strips, examples, and practice activities
What is a Fraction?
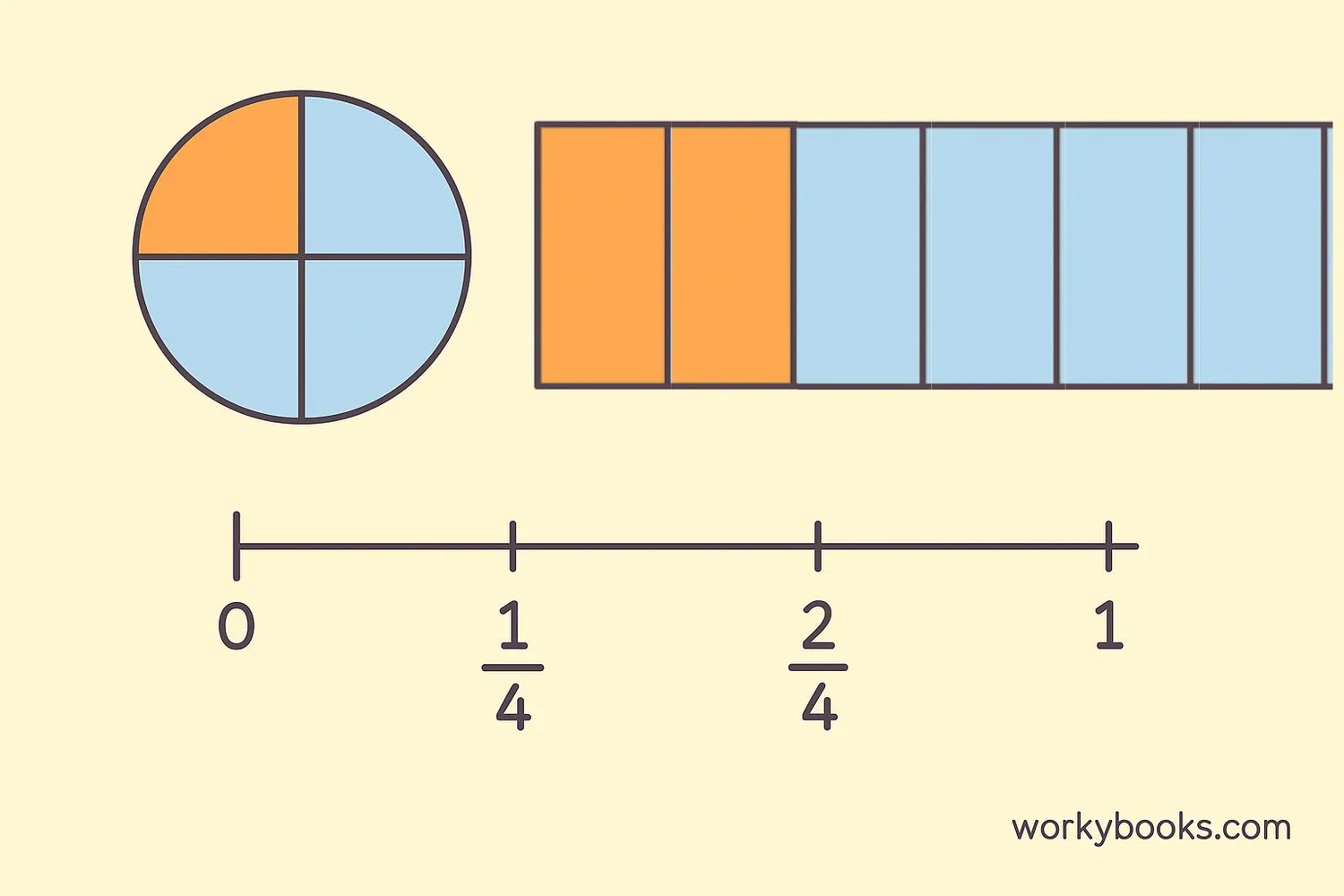
A fraction represents a part of a whole. When we divide something into equal parts, a fraction tells us how many of those parts we're talking about.
Think about a pizza. If you cut it into 8 equal slices and eat 3 slices, you've eaten 3/8 of the pizza. The fraction 3/8 tells us about the parts (3 slices) compared to the whole (8 slices).
Fractions are everywhere in our daily lives - when we share food, measure ingredients for recipes, or tell time ("quarter past three" means 15 minutes past 3, or 1/4 of an hour).
Key Concept
A fraction represents equal parts of a whole. The numerator (top number) tells how many parts we have, and the denominator (bottom number) tells how many equal parts make the whole.
Parts of a Fraction

Every fraction has two parts:
Numerator: The top number that tells how many parts we have.
Denominator: The bottom number that tells how many equal parts make the whole.
For example, in the fraction 2/5:
- The numerator is 2 (we have 2 parts)
- The denominator is 5 (the whole is divided into 5 equal parts)
The fraction bar between the numerator and denominator means "divided by." So 2/5 means 2 divided by 5.
Fraction Formula
The numerator counts the parts, the denominator names the size of the parts.
Remember
The denominator can never be zero because we cannot divide something into zero parts.
Types of Fractions
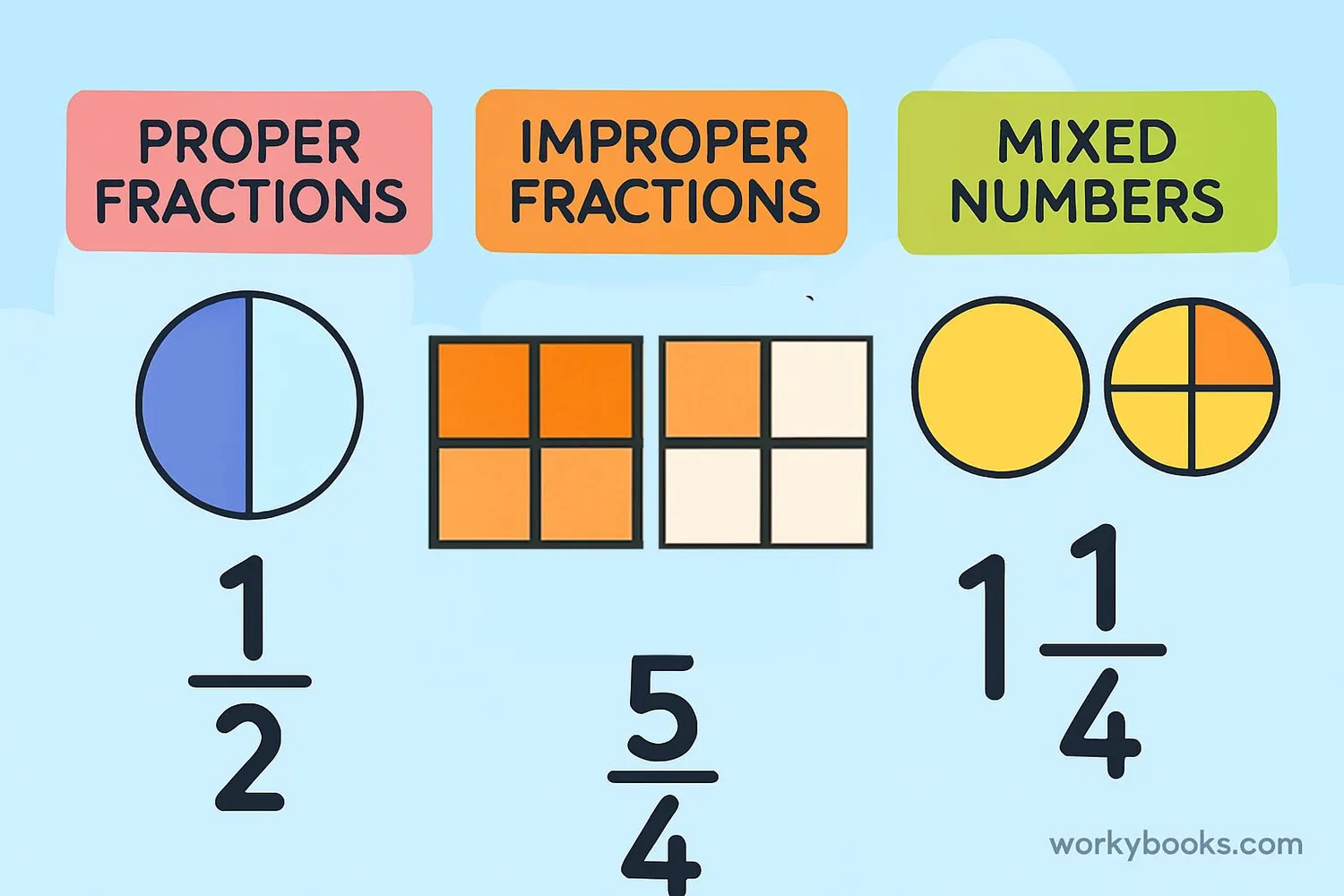
There are different types of fractions:
Proper Fractions: The numerator is smaller than the denominator (e.g., 2/3, 3/5). These represent less than a whole.
Improper Fractions: The numerator is equal to or larger than the denominator (e.g., 5/4, 7/7). These represent a whole or more than a whole.
Mixed Numbers: A whole number combined with a proper fraction (e.g., 1 1/2, 2 3/4). These also represent more than a whole.
We can convert between improper fractions and mixed numbers:
To convert 7/4 to a mixed number: 7 ÷ 4 = 1 with remainder 3, so 1 3/4.
To convert 2 1/3 to an improper fraction: (2 × 3) + 1 = 7, so 7/3.
| Type | Example | Meaning |
|---|---|---|
| Proper Fraction | 3/4 | Less than one whole |
| Improper Fraction | 5/4 | More than one whole |
| Mixed Number | 1 1/4 | One whole plus one quarter |
Conversion Tip
To convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient is the whole number, and the remainder becomes the numerator of the fraction part.
Equivalent Fractions
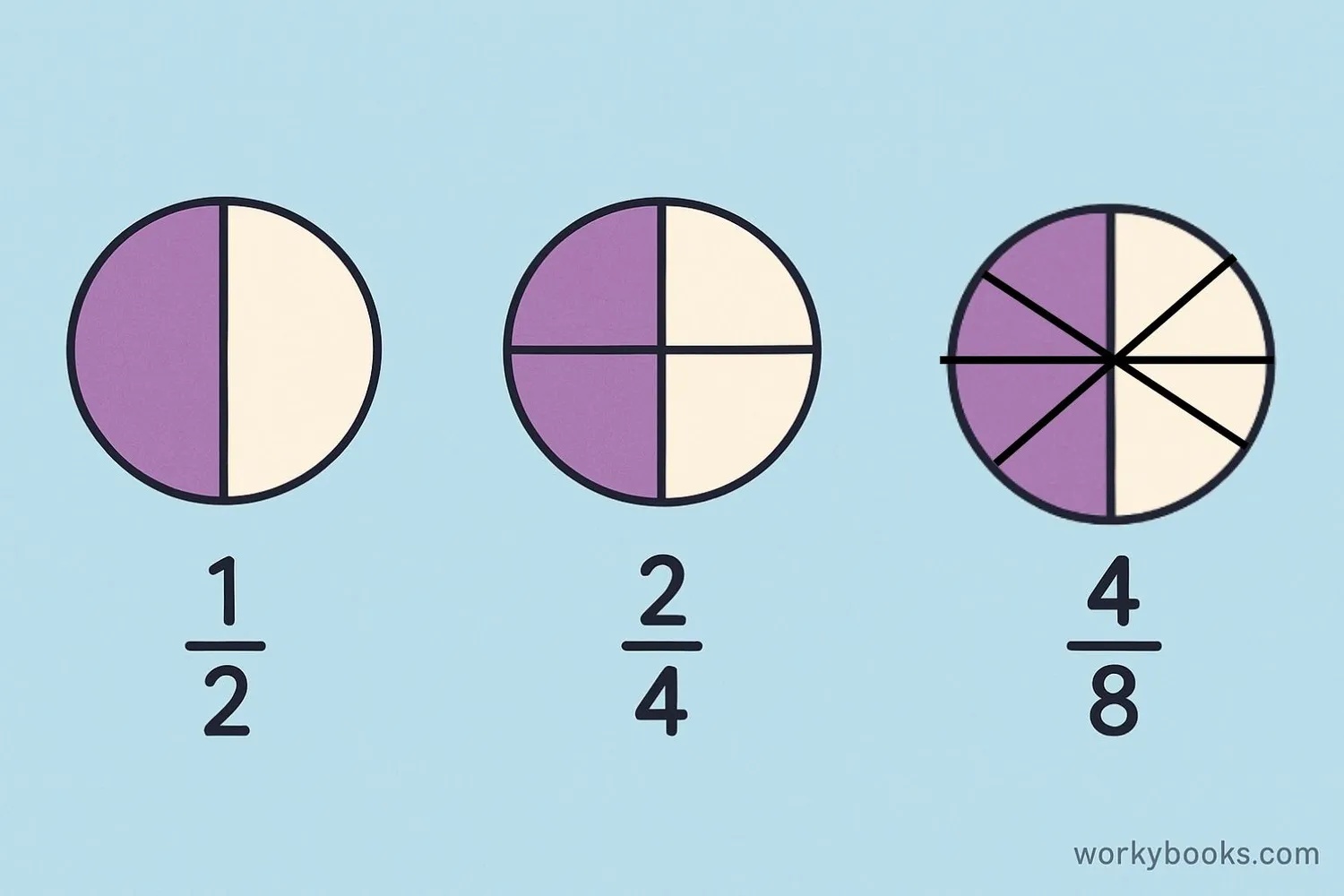
Equivalent fractions are different fractions that represent the same value or amount. For example, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent the same amount - half of a whole.
We can create equivalent fractions by multiplying or dividing both the numerator and denominator by the same number (but not zero!).
Example: To find fractions equivalent to 2/3:
2/3 = 4/6 (multiply numerator and denominator by 2)
2/3 = 6/9 (multiply numerator and denominator by 3)
2/3 = 8/12 (multiply numerator and denominator by 4)
Simplifying fractions means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. For example, 4/8 can be simplified to 1/2 by dividing both numerator and denominator by 4.
Key Concept
Equivalent fractions represent the same value even though they look different. You can create them by multiplying or dividing both the numerator and denominator by the same number.
Comparing Fractions
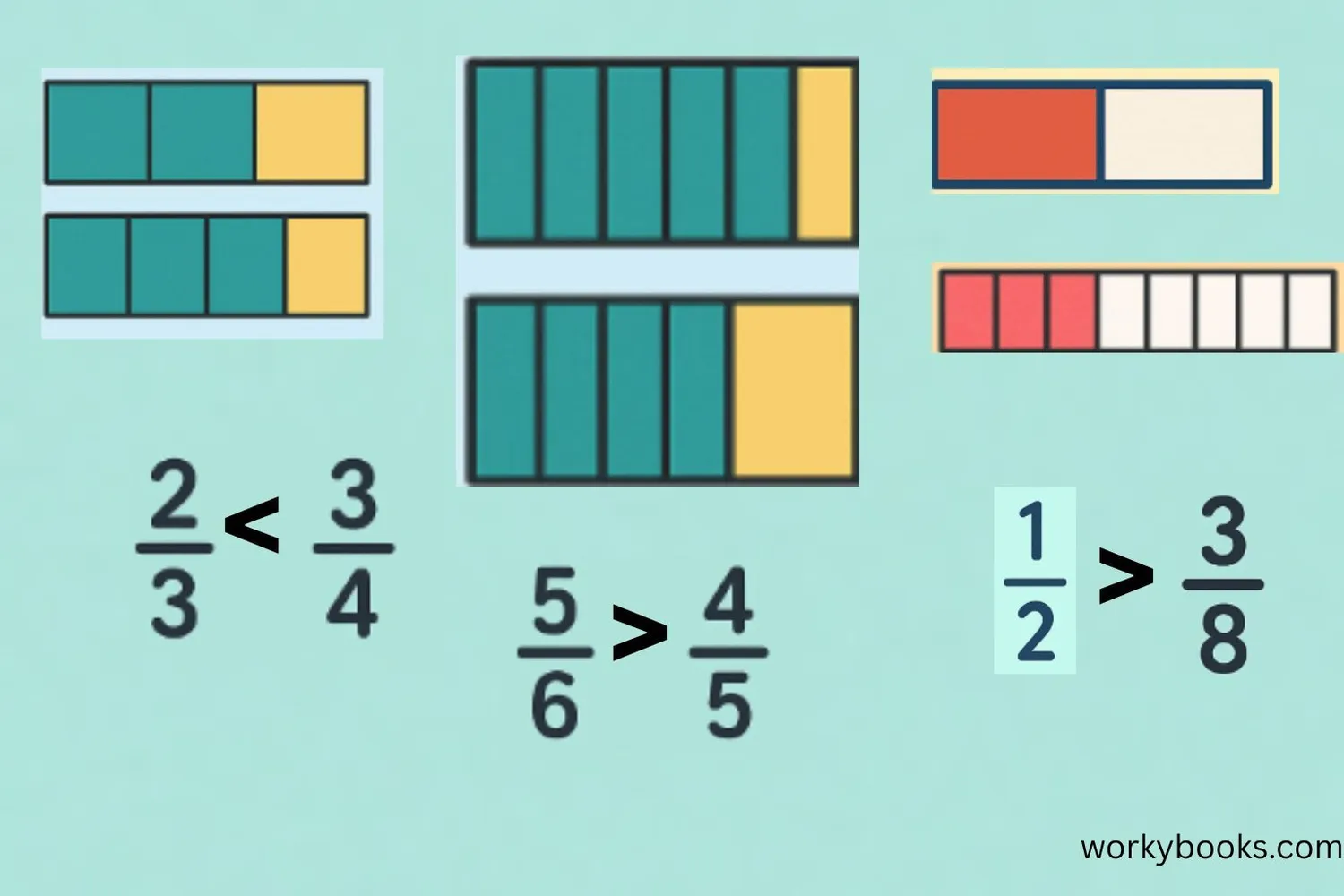
We can compare fractions to see which is larger, smaller, or if they are equal. There are several ways to compare fractions:
Same Denominator: When fractions have the same denominator, the fraction with the larger numerator is larger. For example, 3/5 > 2/5.
Same Numerator: When fractions have the same numerator, the fraction with the smaller denominator is larger. For example, 2/3 > 2/5.
Different Numerators and Denominators: Find a common denominator or use cross multiplication.
To compare 2/3 and 3/4:
Find a common denominator: The least common multiple of 3 and 4 is 12.
2/3 = 8/12 (multiply numerator and denominator by 4)
3/4 = 9/12 (multiply numerator and denominator by 3)
Since 9/12 > 8/12, we know that 3/4 > 2/3.
| Comparison | Method | Result |
|---|---|---|
| 2/5 vs 3/5 | Same denominator | 3/5 > 2/5 |
| 2/3 vs 2/5 | Same numerator | 2/3 > 2/5 |
| 1/2 vs 2/3 | Common denominator | 2/3 > 1/2 |
Comparison Tip
When comparing fractions with different numerators and denominators, finding a common denominator makes it easy to see which fraction is larger.
Fraction Practice Quiz
Test your fraction knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about fractions:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They mainly used unit fractions (fractions with 1 as the numerator) and would express other fractions as sums of unit fractions.
Decimal Connection
Fractions can be converted to decimals by dividing the numerator by the denominator. For example, 1/2 = 0.5, 1/4 = 0.25, and 3/4 = 0.75. This connection helps us understand both representations.
Word Origin
The word "fraction" comes from the Latin word "fractus" which means "broken." This makes sense because fractions represent broken or divided parts of a whole.
Fractions in Music
Fractions are used in music to represent note values. A whole note gets 4 beats, a half note gets 2 beats, a quarter note gets 1 beat, and an eighth note gets half a beat.


