Fractions Greater Than One - Definition, Examples, Quiz, FAQ, Trivia
Learn about improper fractions and mixed numbers with visual models and practice activities
What Are Fractions Greater Than One?
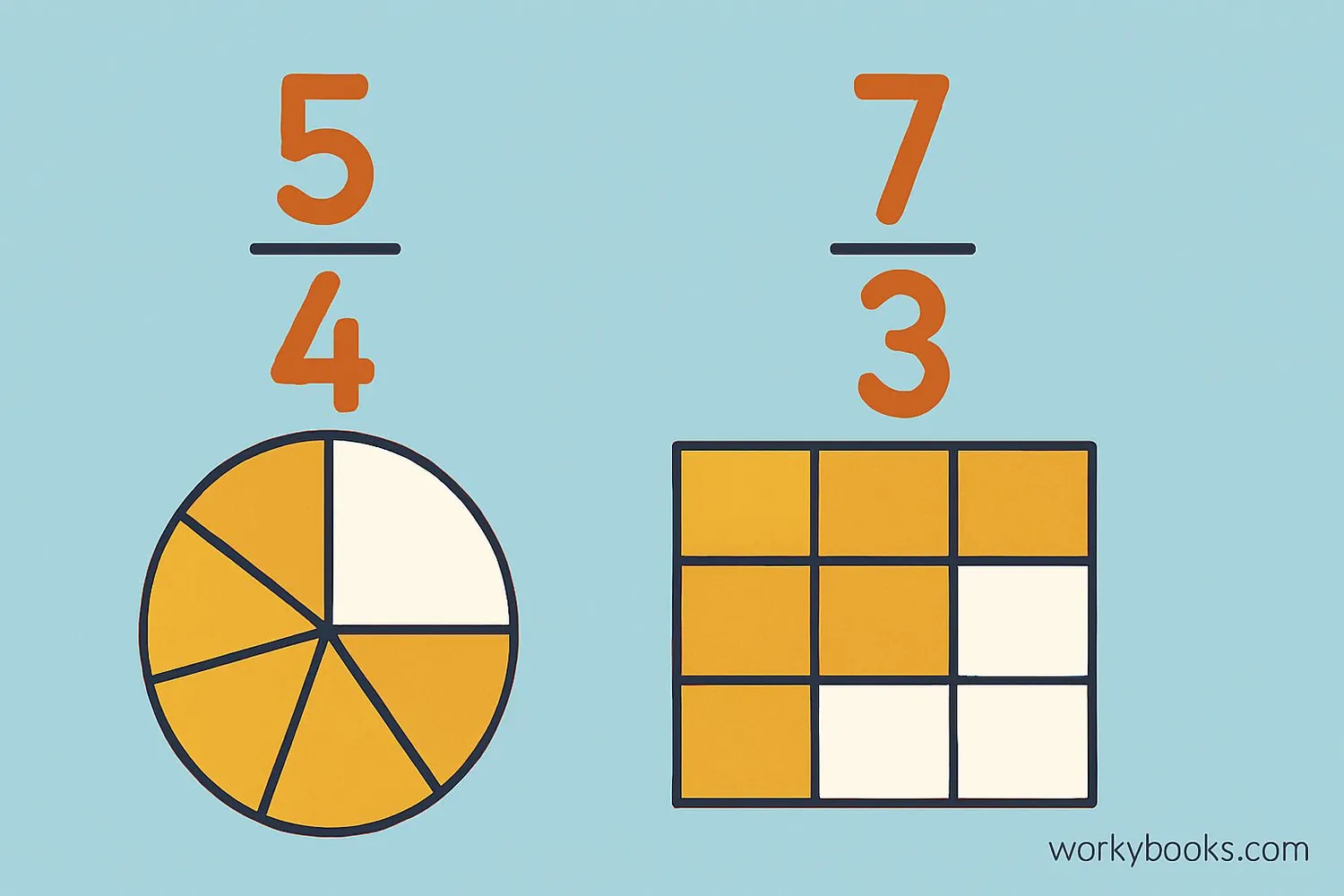
A fraction greater than one is when the numerator (top number) is larger than the denominator (bottom number). This means we have more than one whole!
For example, the fraction 54 is greater than one because 5 is larger than 4. This means we have 5 parts when we only need 4 to make a whole.
Fractions greater than one can be written as improper fractions or mixed numbers. An improper fraction has a numerator larger than the denominator, like 73. A mixed number has a whole number and a fraction, like 2 13.
Key Concept
A fraction is greater than one when its numerator is larger than its denominator. This means we have more than one whole.
Improper Fractions

An improper fraction is a fraction where the numerator is equal to or greater than the denominator. These fractions represent a value greater than or equal to one whole.
Examples of improper fractions:
• 54 (five-fourths) - This is greater than one because 5 > 4
• 73 (seven-thirds) - This is greater than one because 7 > 3
• 88 (eight-eighths) - This equals exactly one whole
Improper fractions are useful in mathematics because they're often easier to work with in calculations than mixed numbers.
Remember
In an improper fraction, the numerator is equal to or larger than the denominator. This doesn't mean the fraction is "wrong" - it's just another way to represent numbers greater than or equal to one.
Mixed Numbers

A mixed number combines a whole number and a proper fraction. Mixed numbers are another way to represent fractions greater than one.
Examples of mixed numbers:
• 1 12 (one and one-half) - This is greater than one
• 2 34 (two and three-quarters) - This is greater than one
• 3 25 (three and two-fifths) - This is greater than one
Mixed numbers are often used in everyday life. For example, when baking, you might need 2 12 cups of flour, which is a mixed number.
Mixed Number Formula
A mixed number combines a whole number with a fraction that is less than one.
Converting Between Improper Fractions and Mixed Numbers

We can convert between improper fractions and mixed numbers. Here's how:
Converting improper fractions to mixed numbers:
1. Divide the numerator by the denominator
2. The quotient becomes the whole number part
3. The remainder becomes the new numerator
4. The denominator stays the same
Example: Convert 73 to a mixed number
Step 1: 7 ÷ 3 = 2 with a remainder of 1
Step 2: Whole number is 2
Step 3: Fraction part is 13
Step 4: Mixed number is 2 13
Converting mixed numbers to improper fractions:
1. Multiply the whole number by the denominator
2. Add the numerator to this product
3. This sum becomes the new numerator
4. The denominator stays the same
Example: Convert 2 13 to an improper fraction
Step 1: 2 × 3 = 6
Step 2: 6 + 1 = 7
Step 3: Numerator is 7
Step 4: Denominator is 3
Improper fraction is 73
Conversion Tip
When converting mixed numbers to improper fractions, remember to multiply the whole number by the denominator before adding the numerator.
Fractions Greater Than One on a Number Line
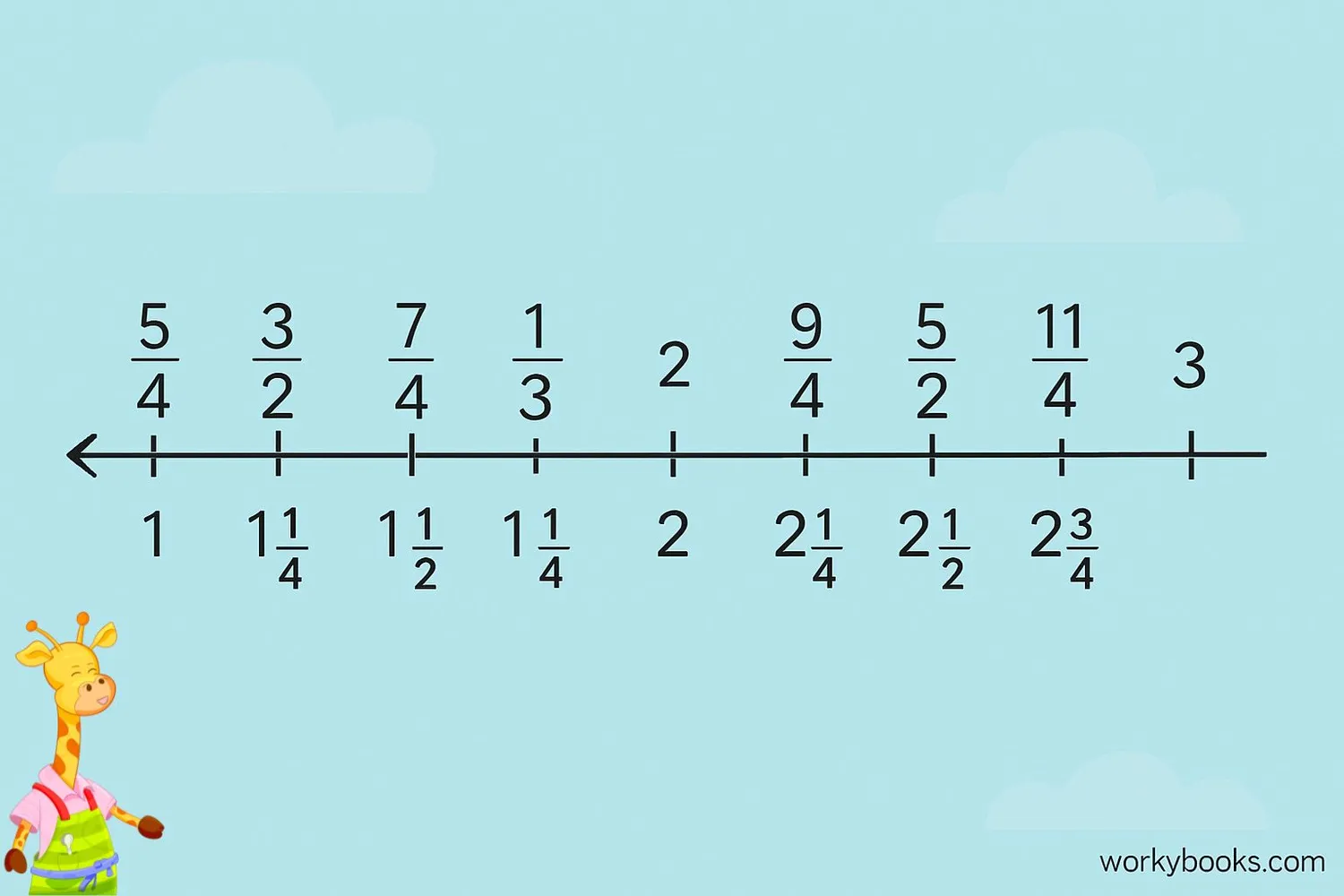
We can represent fractions greater than one on a number line. This helps us visualize their value and compare them to other numbers.
To place a fraction greater than one on a number line:
1. Identify the whole number part
2. Divide the space between that whole number and the next into equal parts based on the denominator
3. Count the appropriate number of parts beyond the whole number
Example: Placing 54 on a number line
Since 54 = 1 14, we find 1 on the number line, then go one-quarter of the way to 2.
Number lines help us see that fractions greater than one are located to the right of 1 on the number line. The further to the right, the larger the value.
Number Line Tip
Fractions greater than one will always be to the right of 1 on the number line. The larger the fraction, the further to the right it will be.
Fraction Practice Quiz
Test your understanding of fractions greater than one with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about fractions greater than one:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they primarily used unit fractions (fractions with 1 as the numerator). They would write other fractions as sums of unit fractions.
Fraction Notation
The horizontal line between numerator and denominator is called a vinculum. This notation was first used by Arabic mathematicians in the 12th century and was later adopted in Europe.
Fraction Words
The word "fraction" comes from the Latin word "fractus" which means "broken." This makes sense because fractions represent parts of a whole—something that has been broken into pieces.
Moon Fractions
Did you know that about 3/4 of the Moon's surface is visible from Earth at different times? This is because of the Moon's libration—a slight wobble in its orbit.


