Heron's Formula - Definition, Examples, Quiz, FAQ, Trivia
Learn to calculate triangle area using side lengths with easy explanations and practice activities
What is Heron's Formula?
Heron's formula is a special mathematical formula that helps us find the area of a triangle when we know the lengths of all three sides. Unlike the basic area formula (½ × base × height), Heron's formula doesn't require knowing the height of the triangle.
This formula is named after Heron of Alexandria, a Greek mathematician and engineer who lived nearly 2,000 years ago. He discovered this useful way to calculate triangle area.
Heron's formula uses the concept of the semi-perimeter (half of the perimeter) of the triangle. This makes the calculation easier and works for all types of triangles - scalene, isosceles, and equilateral.
Heron's Formula
Where s is the semi-perimeter: s = (a+b+c)/2
Key Concept
The semi-perimeter (s) is half the total distance around the triangle. It's the key to using Heron's formula.
How to Use Heron's Formula
Using Heron's formula involves a few simple steps. Let's break it down:
Step-by-Step Process
Let's practice with a simple example:
Example: A triangle has sides of length 5 cm, 6 cm, and 7 cm.
Step 1: a = 5, b = 6, c = 7
Step 2: s = (5 + 6 + 7) ÷ 2 = 18 ÷ 2 = 9
Step 3: s - a = 9 - 5 = 4, s - b = 9 - 6 = 3, s - c = 9 - 7 = 2
Step 4: Multiply: 9 × 4 × 3 × 2 = 216
Step 5: √216 ≈ 14.7
So the area is approximately 14.7 square centimeters.
Remember
Heron's formula works for all triangles, but all side lengths must be positive numbers, and the sum of any two sides must be greater than the third side.
Real-World Examples
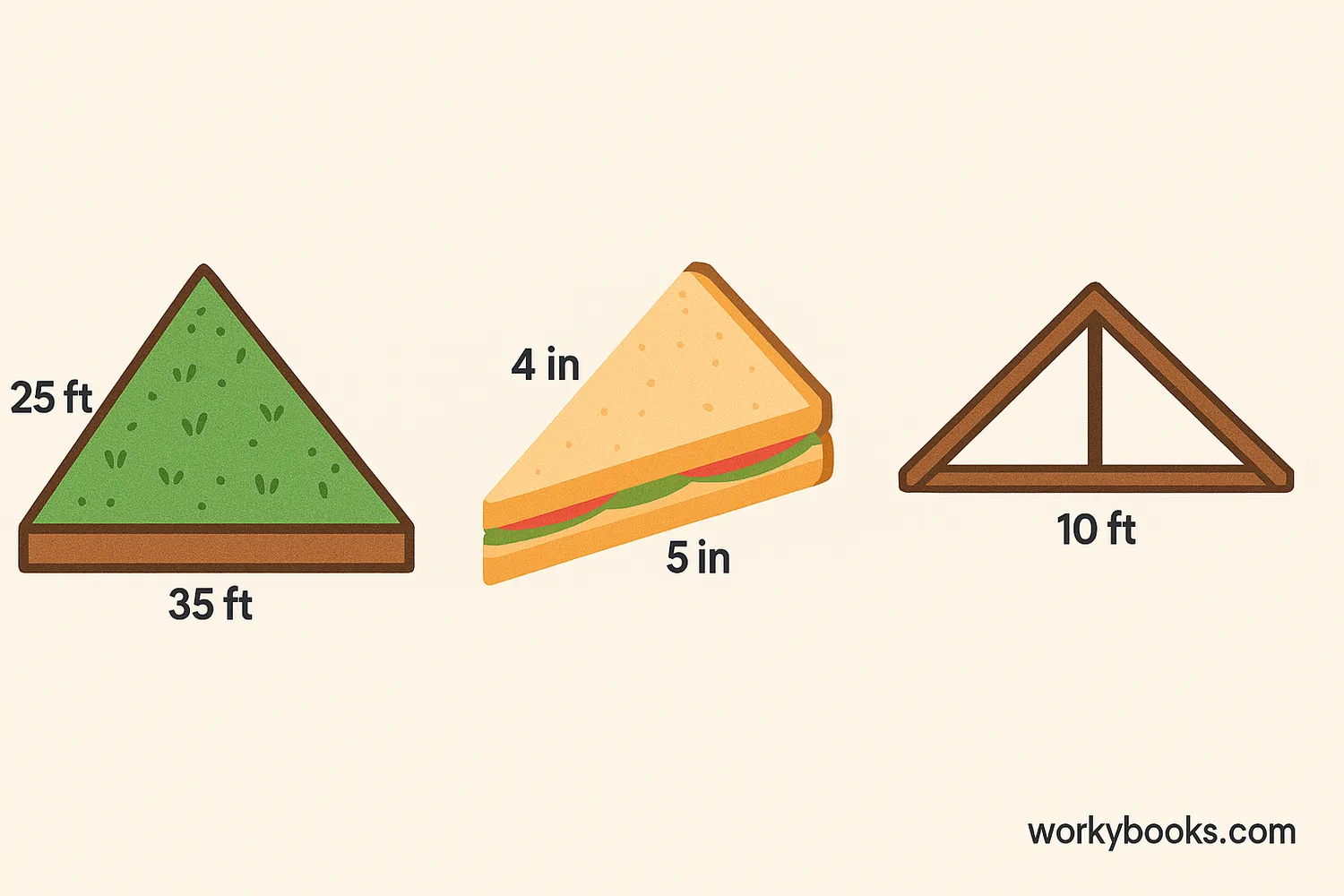
Let's practice using Heron's formula with some real-world examples:
Example 1: A triangular garden has sides measuring 8 m, 15 m, and 17 m. What is its area?
Solution:
s = (8 + 15 + 17) ÷ 2 = 40 ÷ 2 = 20
Area = √[20(20-8)(20-15)(20-17)] = √[20×12×5×3] = √3600 = 60 m²
Example 2: A triangular park has sides of 150 m, 200 m, and 250 m. Find its area.
Solution:
s = (150 + 200 + 250) ÷ 2 = 600 ÷ 2 = 300
Area = √[300(300-150)(300-200)(300-250)] = √[300×150×100×50] = √225,000,000 = 15,000 m²
Example 3: A triangular flag has sides 30 cm, 30 cm, and 40 cm. Calculate its area.
Solution:
s = (30 + 30 + 40) ÷ 2 = 100 ÷ 2 = 50
Area = √[50(50-30)(50-30)(50-40)] = √[50×20×20×10] = √200,000 ≈ 447.21 cm²
Practice finding triangular objects around you and estimating their side lengths to calculate area!
Common Triangles and Their Areas
| Side Lengths | Semi-perimeter (s) | Area |
|---|---|---|
| 3, 4, 5 | 6 | 6 |
| 5, 5, 6 | 8 | 12 |
| 5, 12, 13 | 15 | 30 |
| 7, 8, 9 | 12 | 26.83 |
| 6, 8, 10 | 12 | 24 |
| 9, 10, 11 | 15 | 42.43 |
Practice Tip
Notice how right triangles (like 3-4-5 and 5-12-13) have nice whole number areas? This is a special property of Pythagorean triples!
Practice Quiz
Test your understanding of Heron's formula with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about Heron's formula:
Math Trivia
Discover interesting facts about triangles and mathematics:
Ancient Discovery
Although named after Heron of Alexandria, evidence suggests that Archimedes may have known about this formula more than 200 years earlier. Heron documented it in his book "Metrica," which was lost for centuries until rediscovered in 1896.
Triangle Inequality
For three lengths to form a triangle, they must satisfy the triangle inequality theorem: the sum of any two sides must be greater than the third side. If this isn't true, the "triangle" wouldn't be able to close, and Heron's formula wouldn't work.
Calculation Shortcut
For equilateral triangles (where all sides are equal), Heron's formula simplifies to: Area = (√3/4) × side². This is much easier to calculate than the full Heron's formula for these special triangles.
Practical Applications
Heron's formula is used in computer graphics and CAD software to calculate surface areas of 3D models. It's also used in navigation and surveying to calculate areas of triangular plots of land when only side measurements are available.


