Hexadecimal to Decimal Conversion - Definition, Examples, Quiz, FAQ, Trivia
Learn to convert between hexadecimal and decimal number systems with easy explanations and practice activities
What is Hexadecimal?

Hexadecimal is a number system that uses 16 symbols instead of the 10 symbols used in the decimal system. The word "hexadecimal" comes from "hexa" meaning six and "decem" meaning ten.
The hexadecimal system uses these 16 symbols:
Why do we need hexadecimal? Computers use binary (0s and 1s) which can be very long and hard to read. Hexadecimal is a shorter way to represent binary numbers. Each hexadecimal digit represents 4 binary digits (bits).
Hexadecimal is often used in computer programming, web design (color codes), and memory addressing.
Key Concept
Hexadecimal uses 16 symbols: 0-9 and A-F, where A=10, B=11, C=12, D=13, E=14, F=15.
How to Convert Hexadecimal to Decimal
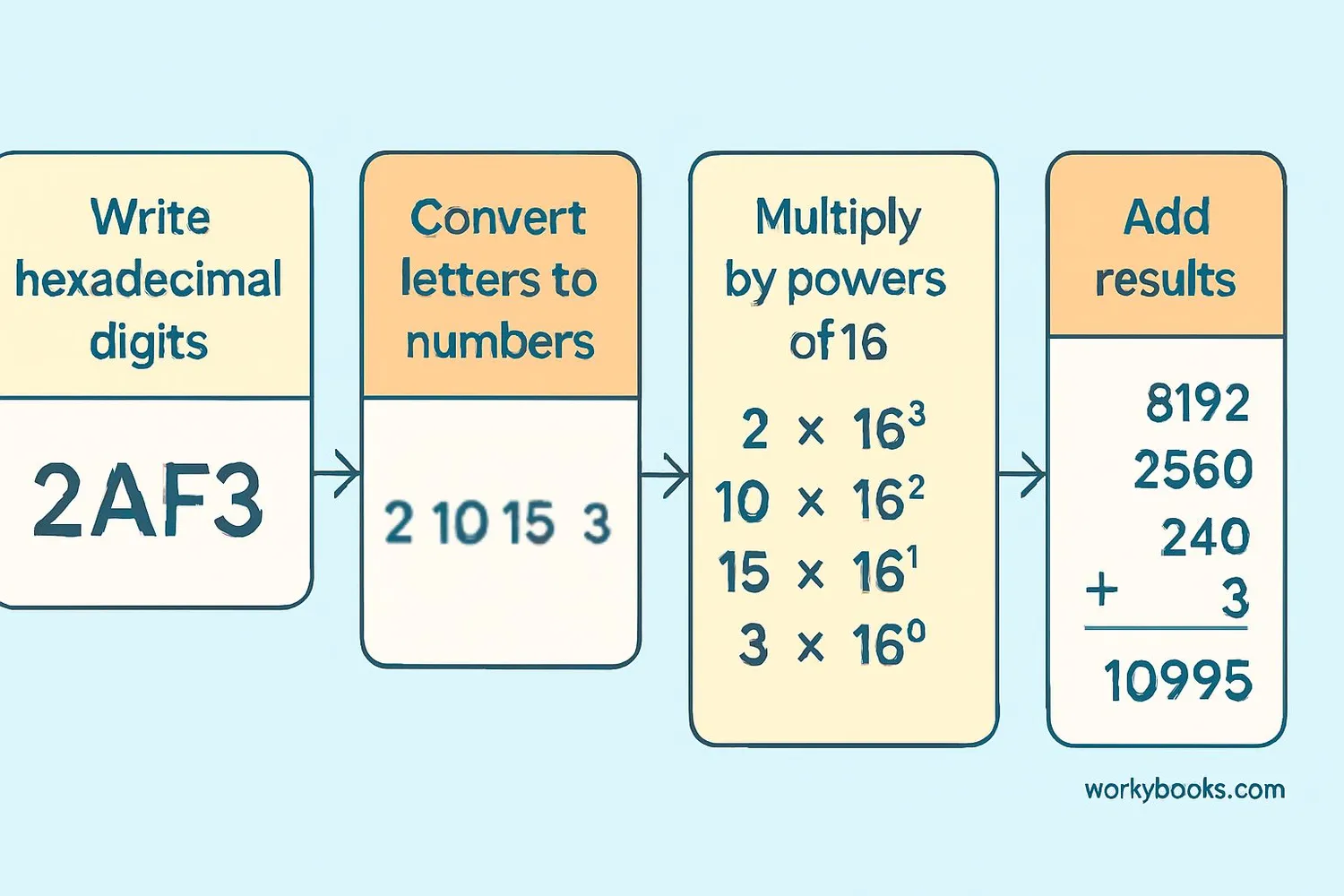
Converting hexadecimal to decimal follows a simple process using powers of 16. Each digit in a hexadecimal number represents a power of 16, starting from the right.
Conversion Formula
Multiply each digit by 16 raised to its position power (starting from 0 on the right), then sum all values.
Example: Convert 2A hexadecimal to decimal
Step 1: Write the digits → 2 and A
Step 2: Convert letters to numbers → A = 10
Step 3: Multiply by powers of 16 → 2×16¹ + 10×16⁰
Step 4: Calculate the result → 32 + 10 = 42
So 2A hexadecimal equals 42 decimal. It's that simple!
Remember
When converting hexadecimal to decimal, remember that the rightmost digit represents 16⁰ (which is 1), the next represents 16¹ (16), then 16² (256), and so on.
Hexadecimal to Decimal Conversion Charts

Conversion charts help us quickly find equivalent values without calculating each time. Here are useful charts for converting hexadecimal to decimal:
Single Digit Hexadecimal to Decimal Chart
| Hexadecimal | Decimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
Two-Digit Hexadecimal to Decimal Conversion Chart
| Hexadecimal | Decimal |
|---|---|
| 10 | 16 |
| 20 | 32 |
| 30 | 48 |
| 40 | 64 |
| 50 | 80 |
| 60 | 96 |
| 70 | 112 |
| 80 | 128 |
| 90 | 144 |
| A0 | 160 |
| B0 | 176 |
| C0 | 192 |
| D0 | 208 |
| E0 | 224 |
| F0 | 240 |
| FF | 255 |
Chart Tip
Notice how each increase of 1 in the left hexadecimal digit adds 16 to the decimal value? You can use this pattern to estimate conversions!
Real-World Examples
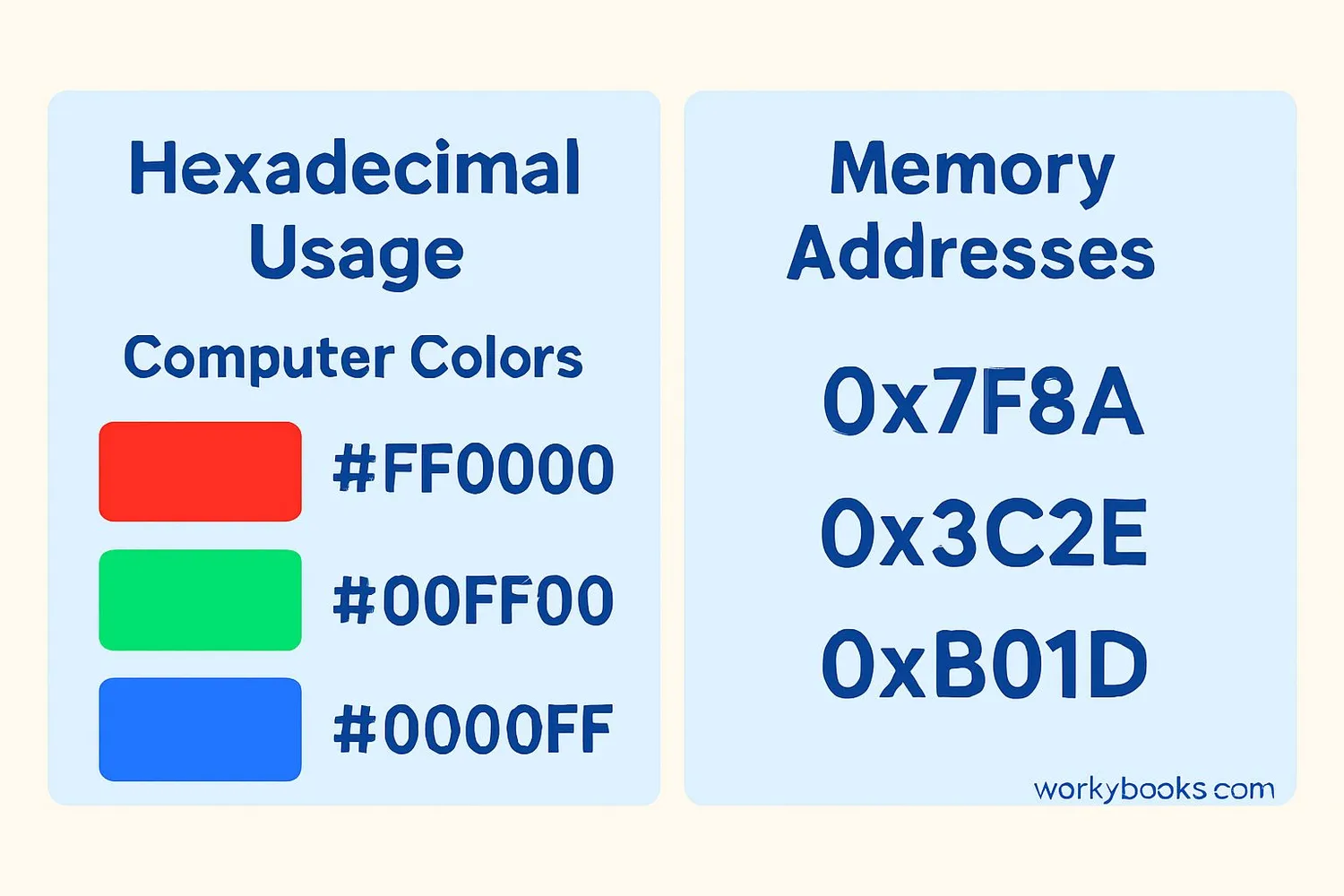
Let's practice conversion with some real-world examples:
Example 1: Convert the hexadecimal color code #FF0000 to decimal values
Solution: FF = 255, 00 = 0, 00 = 0 → RGB(255, 0, 0) which is red
Example 2: A memory address is given as 1F hexadecimal. What is its decimal value?
Solution: 1×16¹ + 15×16⁰ = 16 + 15 = 31
Example 3: Convert B4 hexadecimal to decimal
Solution: B = 11, 4 = 4 → 11×16¹ + 4×16⁰ = 176 + 4 = 180
Example 4: Convert the hexadecimal number 3E8 to decimal
Solution: 3×16² + 14×16¹ + 8×16⁰ = 3×256 + 14×16 + 8×1 = 768 + 224 + 8 = 1000
Practice converting hexadecimal values you might encounter in computer settings or color codes!
Conversion Tip
When converting larger hexadecimal numbers, break them down digit by digit and use the powers of 16 method.
Conversion Practice Quiz
Test your conversion skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about hexadecimal to decimal conversion:
Number System Trivia
Discover interesting facts about number systems:
Origin of Hexadecimal
The hexadecimal system was first introduced in the 1950s by computer scientists working on the IBM 704 system. They needed a more convenient way to represent binary numbers for debugging purposes.
Color Codes
Web colors use hexadecimal codes to represent RGB values. #RRGGBB where RR is red, GG is green, and BB is blue intensity. For example, #FF0000 is pure red, #00FF00 is pure green, and #0000FF is pure blue.
Memory Addressing
Computer memory addresses are often displayed in hexadecimal because it's more compact than binary. A 32-bit address in binary would have 32 digits, but in hexadecimal it only has 8 digits (each hex digit represents 4 bits).
Powers of 16
In hexadecimal, each position represents a power of 16, just like each position in decimal represents a power of 10. The rightmost digit is 16⁰ (1), next is 16¹ (16), then 16² (256), 16³ (4096), and so on.





