Hexagon - Definition, Examples, Quiz, FAQ, Trivia
Learn about hexagons with easy explanations, properties, examples, and interactive quizzes
What is a Hexagon?
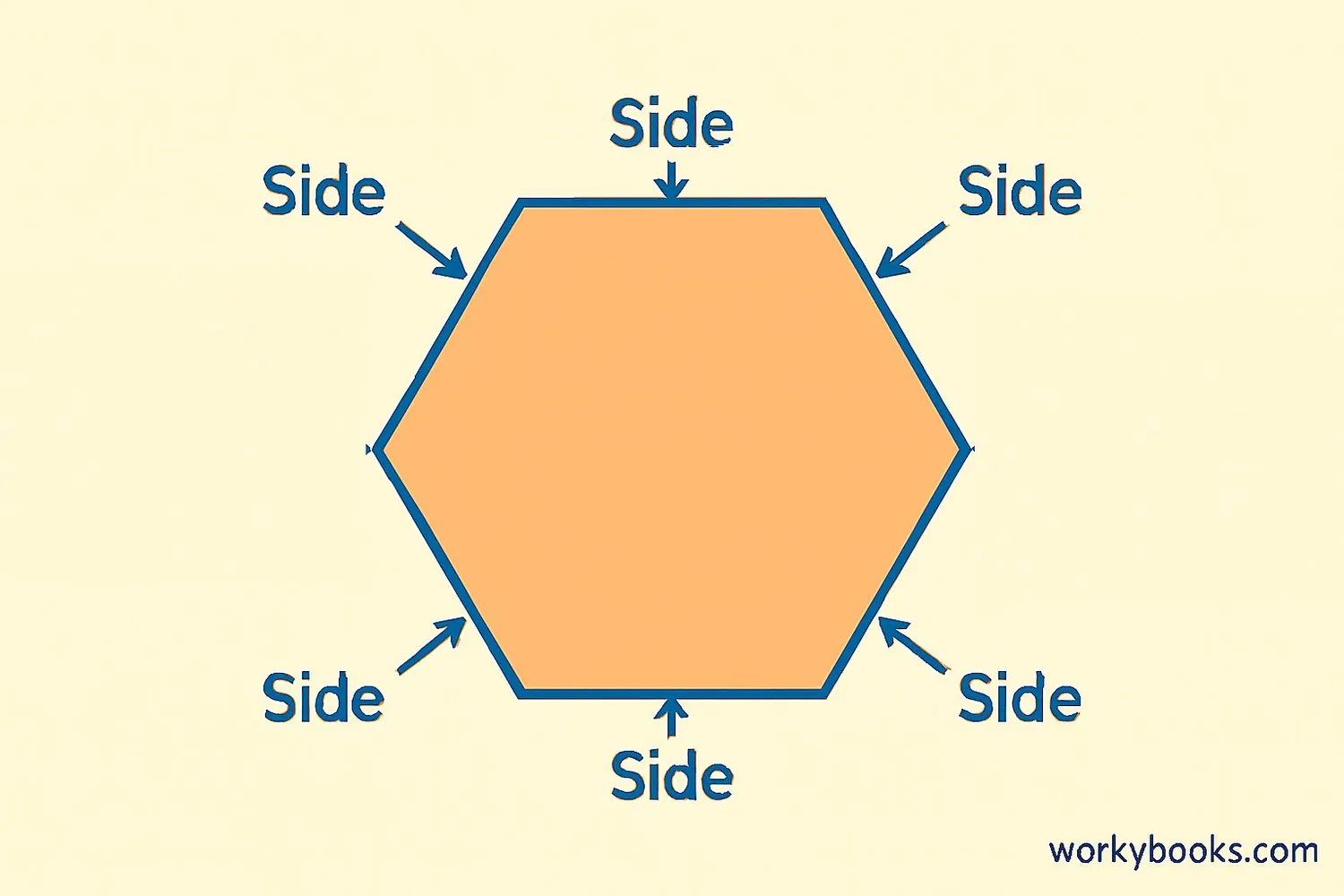
A hexagon is a six-sided polygon with six angles. The word "hexagon" comes from the Greek words "hex" meaning six and "gonia" meaning angle.
Hexagons are fascinating shapes that appear frequently in nature, from honeycombs to snowflakes. They're also used in human-made designs like tiles and bolts.
All hexagons have six straight sides that connect to form a closed shape. The sides can be equal or different lengths, and the angles can be equal or different sizes.
Key Concept
Hexagon = "hexa" (six) + "gon" (angle/side). All hexagons have exactly six sides and six angles.
Properties of a Hexagon
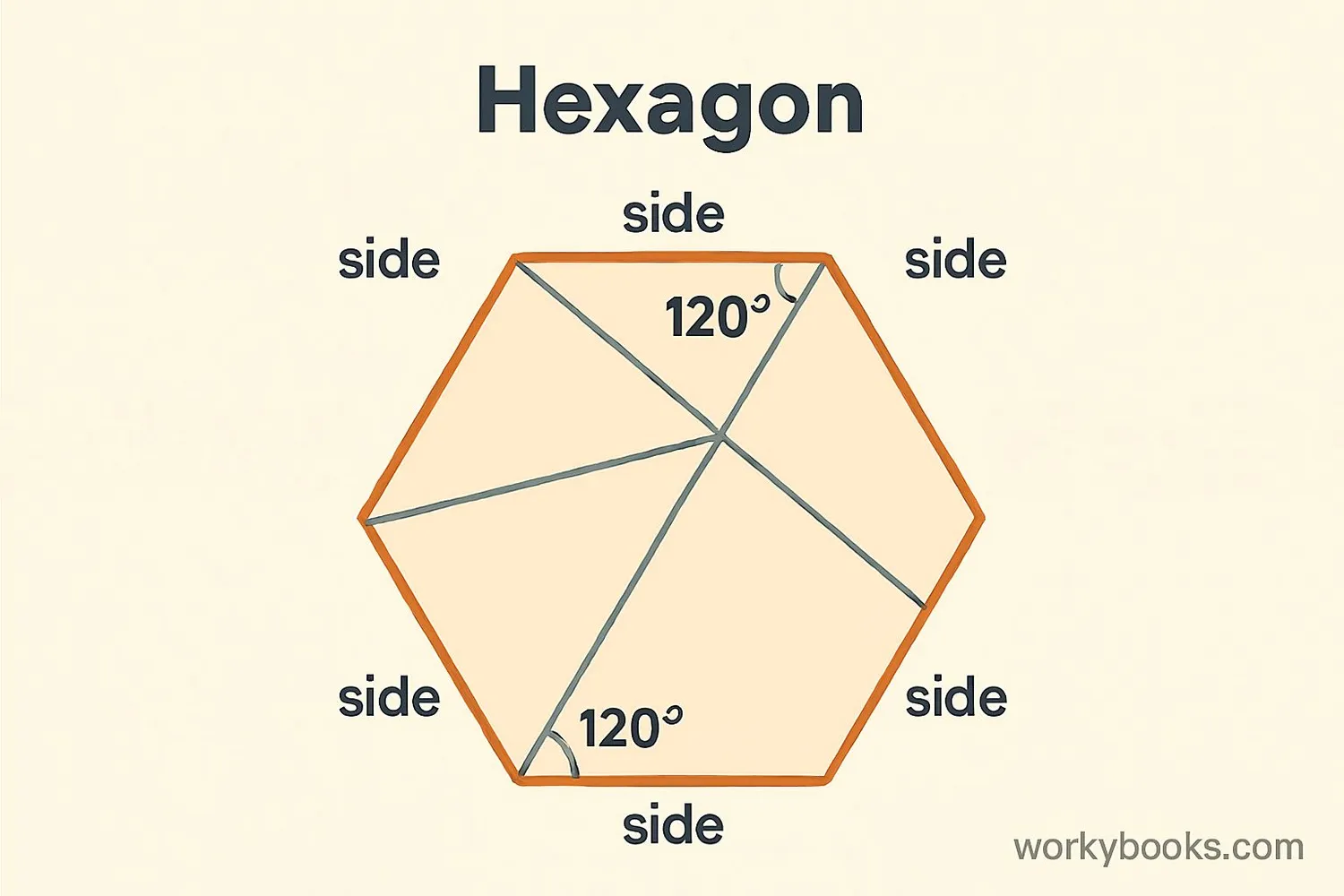
Hexagons have special properties that make them unique among shapes:
- Six sides: All hexagons have exactly six straight sides
- Six angles: Every hexagon has six interior angles
- Sum of interior angles: The angles inside any hexagon always add up to 720 degrees
- Sum of exterior angles: The angles outside a hexagon always add up to 360 degrees
- Nine diagonals: A hexagon has nine diagonals (lines connecting non-adjacent vertices)
Remember
You can find the sum of interior angles for any polygon using the formula: (n-2) × 180°, where n is the number of sides. For a hexagon: (6-2) × 180° = 4 × 180° = 720°.
Regular vs Irregular Hexagons
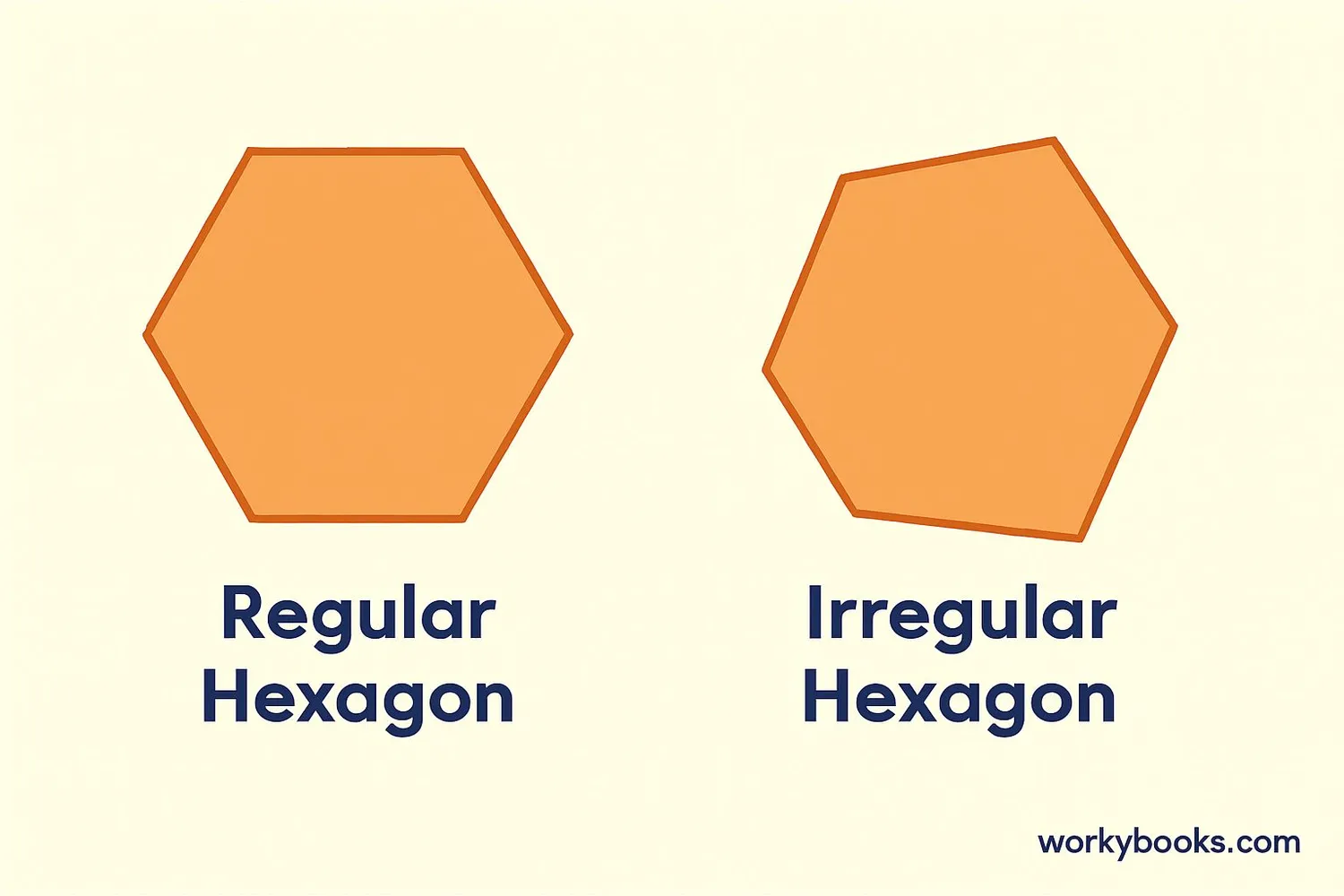
There are two main types of hexagons:
Regular Hexagons: All six sides are equal in length, and all six interior angles are equal (each measuring 120 degrees). Regular hexagons have rotational symmetry and reflection symmetry.
Irregular Hexagons: The sides are not all equal, and the angles are not all equal. Irregular hexagons can take many different forms as long as they have six straight sides.
Real World Example
Honeycombs are made of regular hexagons, while a stop sign is an octagon (8 sides), not a hexagon!
Area and Perimeter of a Hexagon
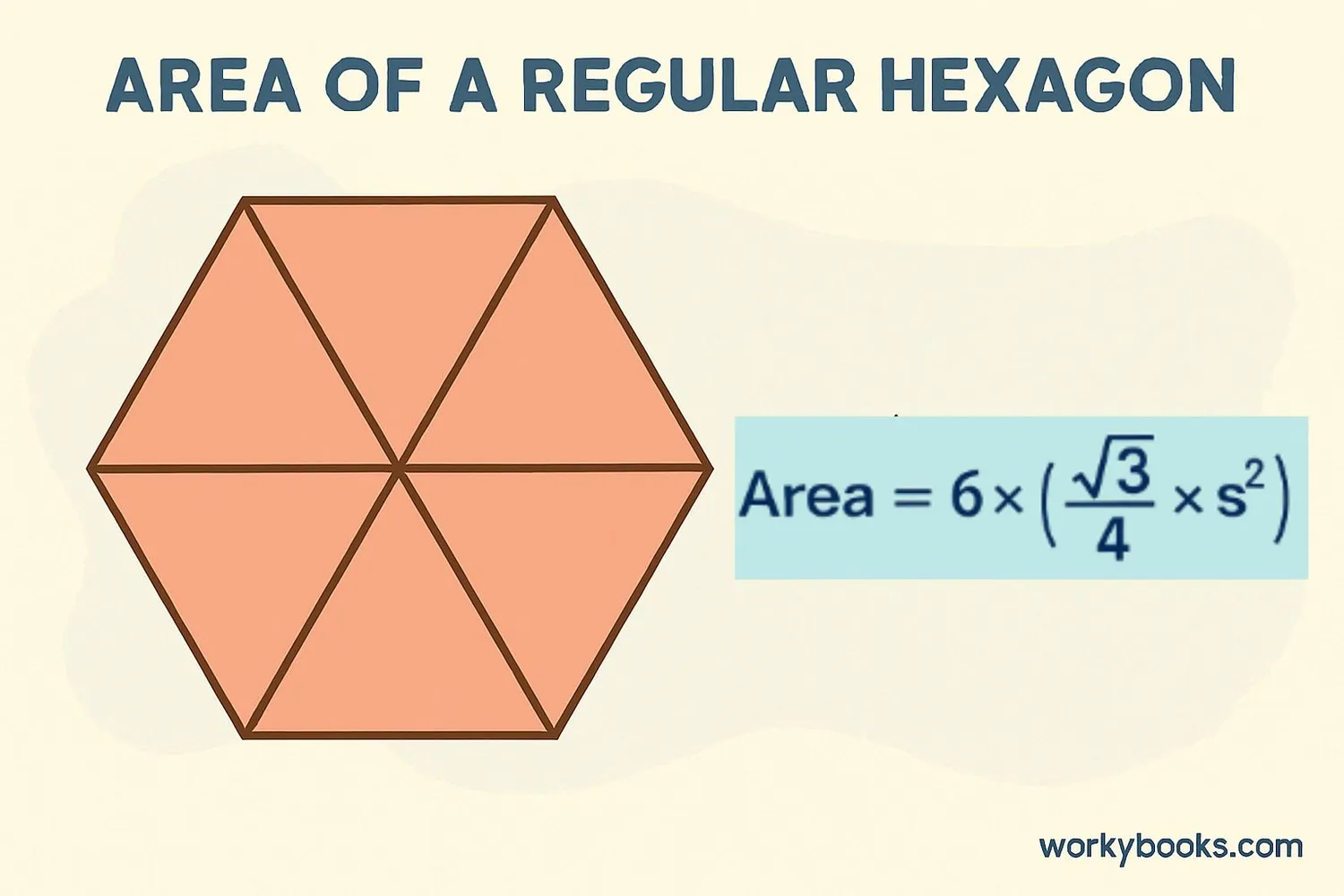
For regular hexagons (where all sides are equal), we have special formulas:
Perimeter Formula
Where s is the length of one side
Area Formula
Where s is the length of one side
Example: Find the perimeter and area of a regular hexagon with side length 4 cm.
Perimeter = 6 × 4 = 24 cm
Area = (3√3 × 4²) ÷ 2 = (3√3 × 16) ÷ 2 = (48√3) ÷ 2 = 24√3 ≈ 41.57 cm²
Remember
These formulas only work for regular hexagons. For irregular hexagons, we need to use different methods to find area and perimeter.
Real-World Examples of Hexagons
Hexagons appear in many places in our world:
In Nature:
- Honeycombs in beehives
- Snowflakes (many have hexagonal patterns)
- Basalt columns at the Giant's Causeway
- Turtle shell patterns
- Nuts and bolts (many have hexagonal heads)
- Floor tiles and paving stones
- Soccer ball patterns (combine hexagons and pentagons)
- Pencils (often have hexagonal cross-sections)
Did You Know
Bees build hexagonal honeycombs because this shape uses the least amount of wax to store the most honey - it's nature's efficient design!
Hexagon Quiz
Test your knowledge about hexagons with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about hexagons:
Hexagon Trivia
Discover interesting facts about hexagons:
Nature's Favorite
Hexagons appear throughout nature more than any other shape. From basalt columns to snowflakes to insect eyes, hexagons are nature's go-to shape for efficiency and strength.
Saturn's Hexagon
Saturn has a persistent hexagonal cloud pattern at its north pole. This giant hexagon is about 30,000 km across and has been observed by spacecraft since the 1980s.
Ancient Recognition
Ancient mathematicians recognized the special properties of hexagons over 2,000 years ago. The regular hexagon features in Euclid's Elements, written around 300 BCE.
Tiling Property
Regular hexagons are one of only three regular polygons that can tile a plane without gaps. The others are equilateral triangles and squares. This is why hexagon tiles are so popular for floors.





