Hexagonal Prism - Definition, Examples, Quiz, FAQ, Trivia
Learn about 3D shapes with easy explanations, properties, formulas, examples, and interactive quizzes
What is a Hexagonal Prism?

A hexagonal prism is a three-dimensional shape that has two parallel hexagonal bases and six rectangular faces connecting the sides of the hexagons. Think of it like a pencil - the body of a pencil is a hexagonal prism!
The word "hexagonal" comes from "hexa" meaning six, and "gon" meaning angles. So a hexagon is a shape with six sides and six angles. A prism is a solid shape that has the same cross-section along its length.
Hexagonal prisms are all around us in everyday life. Nuts and bolts often have hexagonal heads, some pencils are hexagonal, and certain honeycomb cells are hexagonal prisms. Understanding this shape helps us recognize patterns in the world around us.
Key Concept
A hexagonal prism has 8 faces total: 2 hexagonal bases and 6 rectangular lateral faces. It also has 18 edges and 12 vertices.
Properties of a Hexagonal Prism
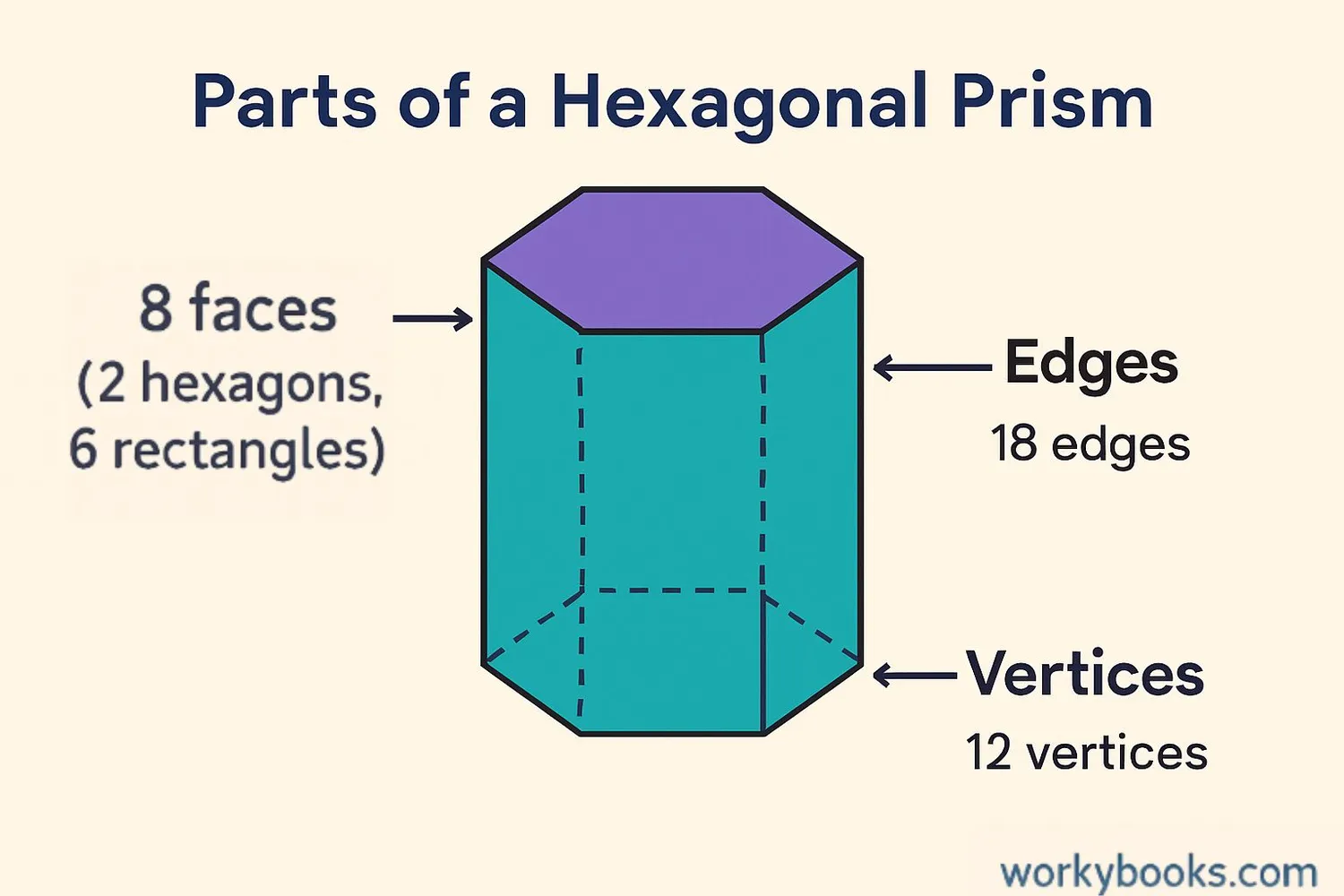
Every 3D shape has special properties that make it unique. Let's explore the properties of a hexagonal prism:
Faces
A hexagonal prism has 8 faces total: 2 hexagonal bases and 6 rectangular lateral faces.
Edges
It has 18 edges - 12 edges from the two hexagons and 6 edges connecting the bases.
Vertices
A hexagonal prism has 12 vertices (corner points) - 6 on each hexagonal base.
Base Shape
The bases are always hexagons (6-sided polygons) and are parallel to each other.
Lateral Faces
The lateral faces (side faces) are always rectangles or parallelograms.
Symmetry
A regular hexagonal prism has rotational symmetry of order 6 and reflection symmetry.
Remember
The lateral faces of a right hexagonal prism are rectangles, while in an oblique hexagonal prism they are parallelograms.
Volume of a Hexagonal Prism
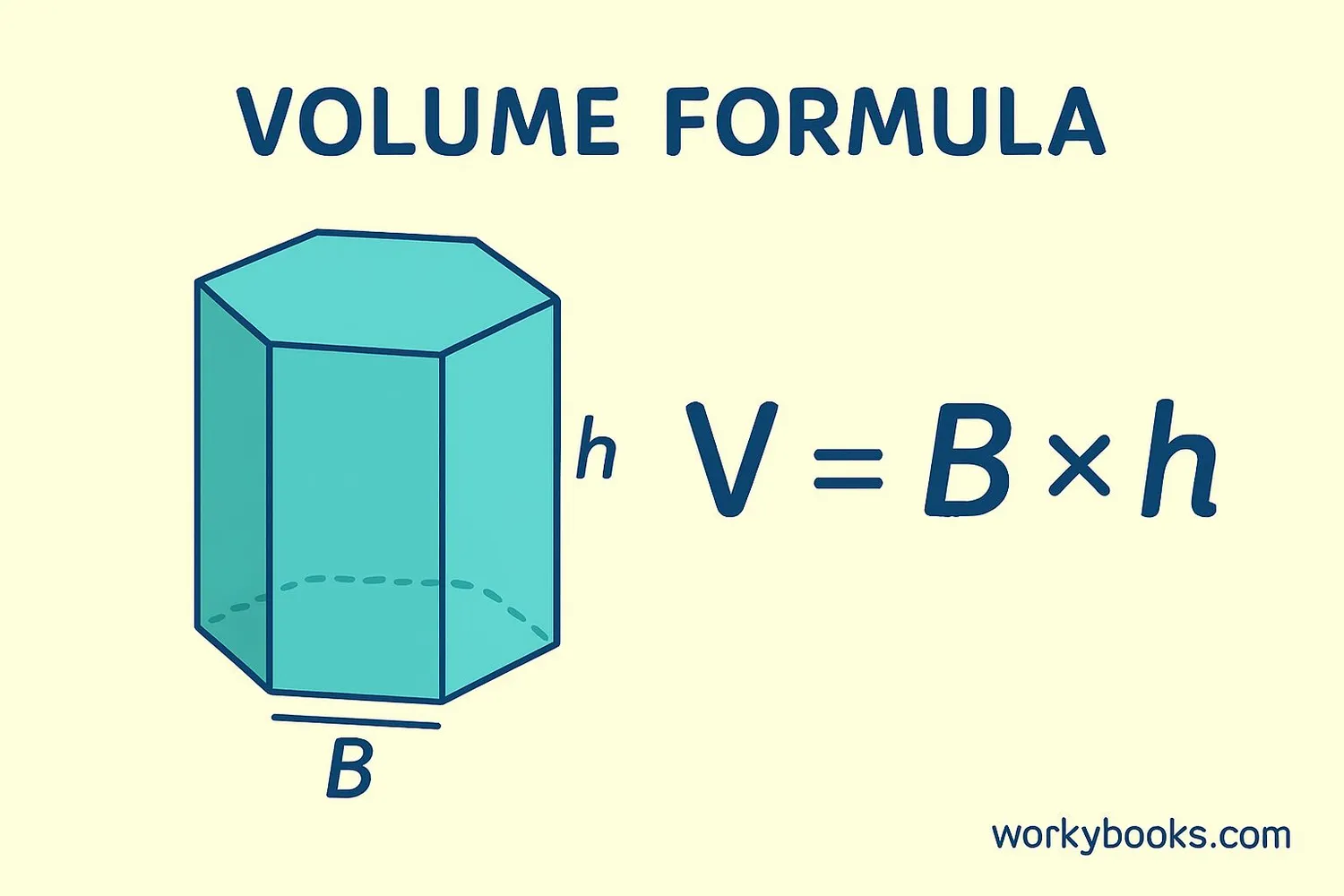
Volume is the amount of space inside a 3D shape. For any prism, the volume can be found by multiplying the area of its base by its height.
Volume Formula
Where:
a = length of one side of the hexagon
h = height of the prism
Example: Find the volume of a hexagonal prism with side length 4 cm and height 10 cm.
Step 1: Calculate the base area: (3√3/2) × 4² = (3√3/2) × 16 = (3 × 1.732/2) × 16 ≈ (5.196/2) × 16 ≈ 2.598 × 16 ≈ 41.57 cm²
Step 2: Multiply by height: 41.57 × 10 = 415.7 cm³
So the volume is approximately 415.7 cubic centimeters.
Remember
Volume is always measured in cubic units (cm³, m³, etc.) because it represents three-dimensional space.
Surface Area of a Hexagonal Prism

Surface area is the total area of all the faces of a 3D shape. For a hexagonal prism, we need to calculate the area of both hexagonal bases and all six rectangular faces.
Surface Area Formula
Where:
a = length of one side of the hexagon
h = height of the prism
Example: Find the surface area of a hexagonal prism with side length 3 cm and height 8 cm.
Step 1: Calculate lateral area: 6 × 3 × 8 = 144 cm²
Step 2: Calculate area of two bases: 2 × (3√3/2 × 3²) = 2 × (3√3/2 × 9) = 2 × (27√3/2) = 27√3 ≈ 27 × 1.732 ≈ 46.76 cm²
Step 3: Add them together: 144 + 46.76 = 190.76 cm²
So the surface area is approximately 190.76 square centimeters.
Remember
Surface area is always measured in square units (cm², m², etc.) because it represents the coverage of surfaces.
Net of a Hexagonal Prism

A net is a 2D pattern that can be folded to form a 3D shape. Imagine taking a cardboard box and cutting along some edges so you can flatten it out - that flattened pattern is the net of the box.
For a hexagonal prism, the net consists of two hexagons (the bases) and six rectangles (the lateral faces) arranged in a specific pattern. When you fold this pattern along the edges, it forms the 3D hexagonal prism.
Understanding nets helps us:
- Visualize 3D shapes in 2D form
- Calculate surface area more easily
- Understand how shapes are constructed
- Create models of 3D shapes from paper or other materials
Try This
Try drawing the net of a hexagonal prism on paper, cut it out, and fold it to create your own 3D model!
Real-World Examples
Hexagonal prisms are all around us! Here are some common examples:
Pencils: Many pencils have a hexagonal cross-section. This shape prevents them from rolling off desks and makes them easier to grip.
Nuts and Bolts: The heads of many nuts and bolts are hexagonal. This allows tools like wrenches to get a good grip for turning.
Honeycombs: Beehives are made of hexagonal prism cells. This shape uses space efficiently and requires less wax than other shapes.
Architecture: Some buildings and structures use hexagonal designs for both aesthetic appeal and structural strength.
Crystals: Some minerals, like quartz, naturally form hexagonal prism shapes as they grow.
Next time you're out and about, see how many hexagonal prisms you can spot in your environment!
Did You Know
Bees build hexagonal cells in their hives because this shape uses the least amount of wax to store the most honey - nature's efficient engineers!
Hexagonal Prism Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about hexagonal prisms:
Geometry Trivia
Discover interesting facts about geometry and hexagonal prisms:
Bee Engineering
Honeybees construct their honeycombs in hexagonal prism shapes because this uses the least amount of wax to create the most storage space. Mathematicians have proven that hexagons are the most efficient shape for dividing a surface into equal areas with minimal perimeter.
Crystal Forms
Many crystals naturally form hexagonal prisms due to their molecular structure. Examples include quartz, beryl (which includes emerald and aquamarine), and apatite. These crystals often have beautiful hexagonal cross-sections.
Euler's Formula
All polyhedra, including hexagonal prisms, follow Euler's formula: F + V - E = 2 (where F is faces, V is vertices, and E is edges). For a hexagonal prism: 8 + 12 - 18 = 2, which confirms the formula!
Ancient Geometry
The study of hexagonal shapes dates back to ancient Greece. The word "hexagon" comes from the Greek words "hex" meaning six and "gonia" meaning angle. Ancient mathematicians were fascinated by the properties of regular polygons including hexagons.





