How to Multiply Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn to multiply fractions with simple steps, visual examples, and practice activities
What is Fraction Multiplication?
Multiplying fractions means finding a part of a part. When we multiply fractions, we're finding a fraction of another fraction. For example, 1/2 of 1/2 is 1/4.
The basic rule for multiplying fractions is simple:
Multiplication Rule
Why do we multiply fractions? We use fraction multiplication in many real-life situations like cooking recipes, dividing land, calculating discounts, and sharing things equally.
Key Concept
Multiplying fractions is actually simpler than adding them because you don't need a common denominator!
How to Multiply Fractions

Let's break down fraction multiplication into simple steps:
Step 1: Multiply the Numerators
The numerator is the top number of the fraction. Multiply the numerators of both fractions together.
(Numerators: 2 and 3)
Step 2: Multiply the Denominators
The denominator is the bottom number of the fraction. Multiply the denominators of both fractions together.
(Denominators: 3 and 4)
Step 3: Form the New Fraction
Put the product of the numerators over the product of the denominators.
Step 4: Simplify the Fraction
Reduce the fraction to its simplest form by dividing both numerator and denominator by their greatest common factor (GCF).
So 6/12 simplifies to 1/2
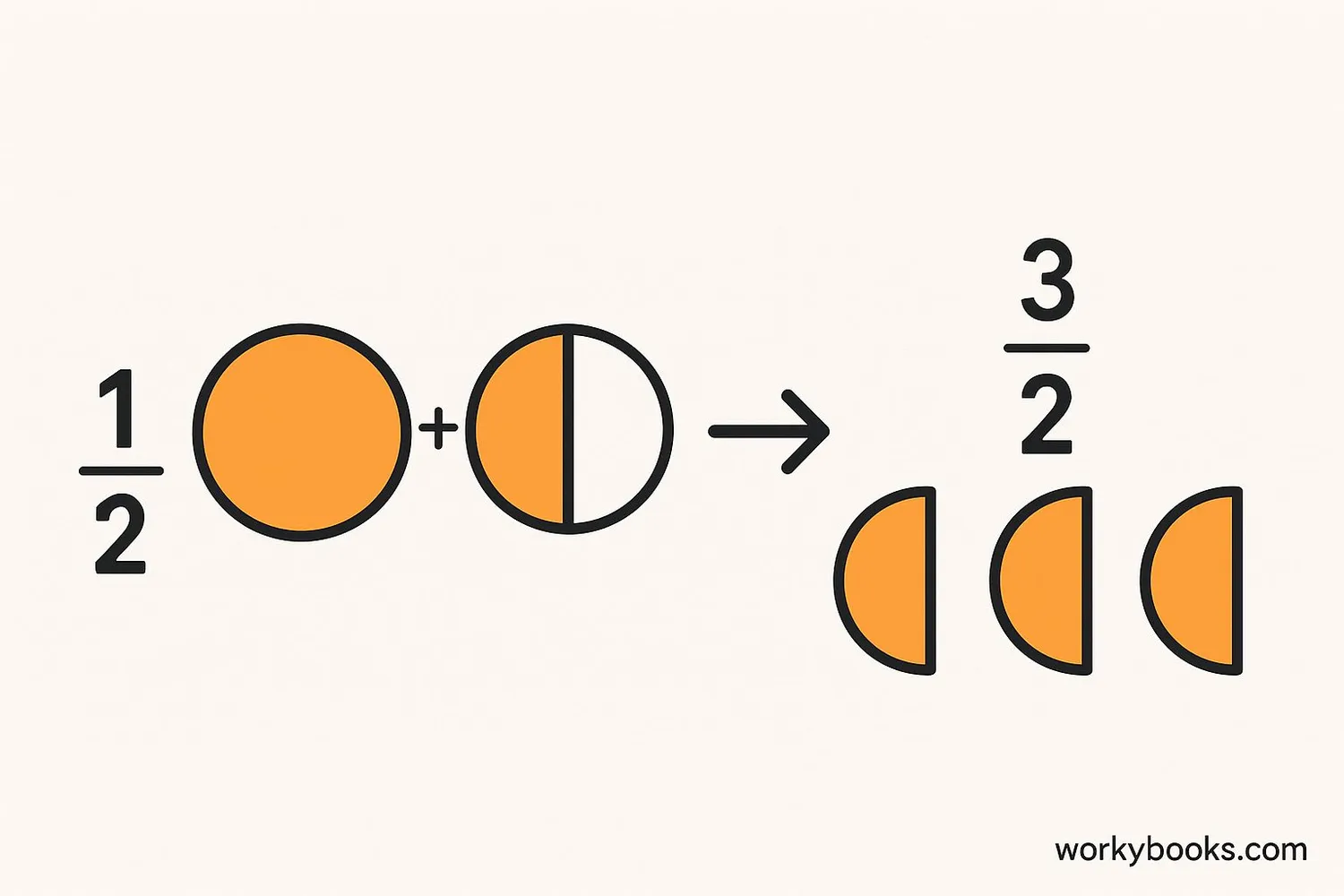
Multiplying a Fraction by a Whole Number
Convert the whole number to a fraction by putting it over 1. For example: 3 × 2/5 = 3/1 × 2/5 = (3×2)/(1×5) = 6/5 = 1 1/5
Multiplying Mixed Numbers
To multiply mixed numbers (like 2 1/2 or 3 3/4), we first convert them to improper fractions:
Step 1: Convert to Improper Fractions
Multiply the whole number by the denominator, then add the numerator. Keep the same denominator.
2 1/2 = (2 × 2 + 1)/2 = 5/2
1 3/4 = (1 × 4 + 3)/4 = 7/4
Step 2: Multiply the Fractions
Multiply the numerators and denominators as with regular fractions.
Step 3: Simplify and Convert Back
Convert the improper fraction back to a mixed number if needed.
Remember
You can simplify before multiplying to make calculations easier. For example, 5/10 × 2/3 = 1/2 × 2/3 = 2/6 = 1/3
Visual Examples
1/2 × 1/2 = 1/4
Half of a half is one-fourth
2/3 × 1/4 = 2/12 = 1/6
Two-thirds of one-fourth is two-twelfths
Let's practice with some real-world examples:
Example 1: A recipe calls for 2/3 cup of flour. You need to make half the recipe. How much flour do you need?
Solution: 1/2 × 2/3 = (1×2)/(2×3) = 2/6 = 1/3 cup
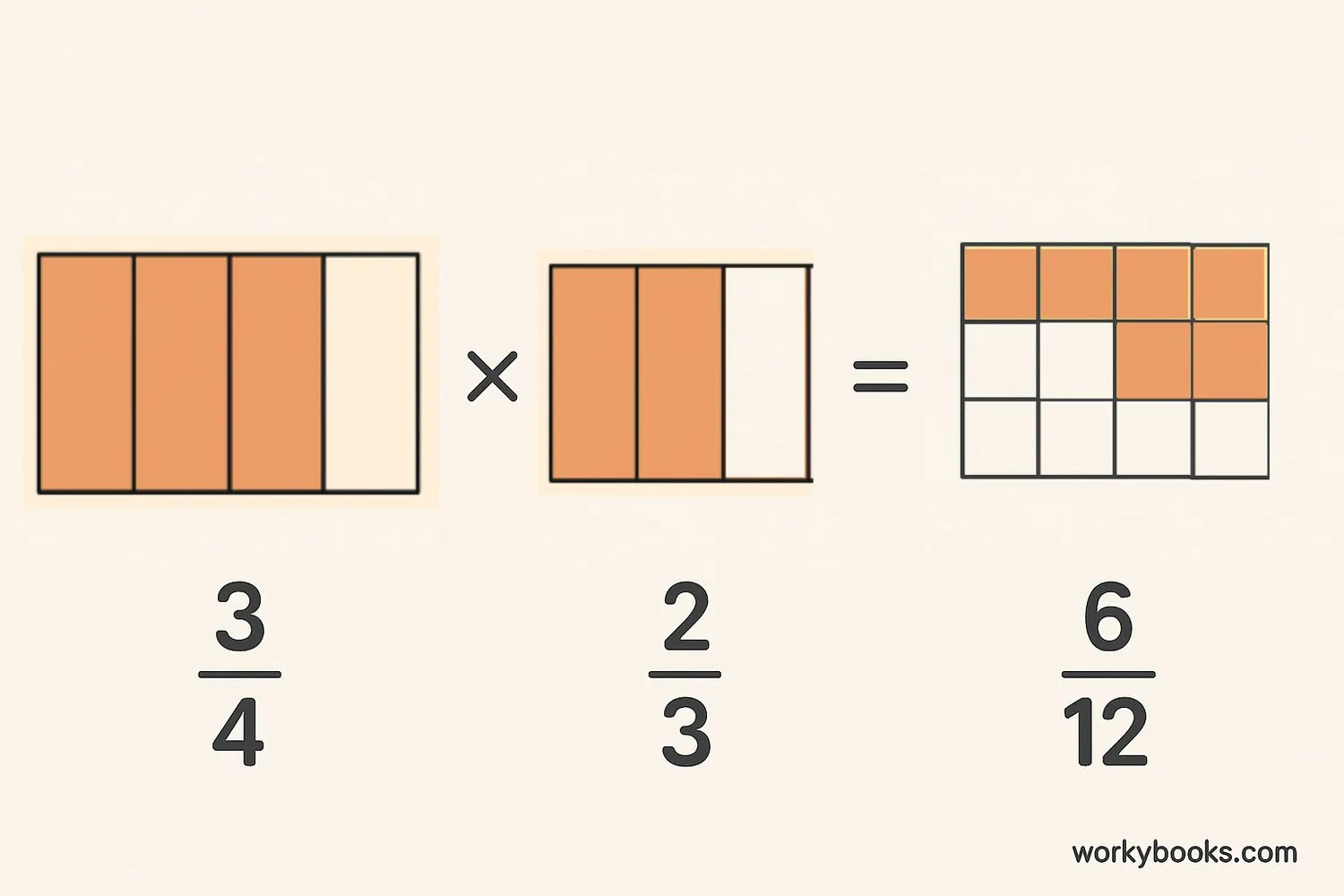
Example 2: You have 3/4 of a pizza left. You eat 2/3 of what's left. How much pizza did you eat?
Solution: 3/4 × 2/3 = (3×2)/(4×3) = 6/12 = 1/2 of the original pizza
Example 3: A piece of fabric is 1 1/2 meters long. You need 3/4 of this length. How much fabric do you need?
Solution: Convert 1 1/2 to 3/2, then 3/2 × 3/4 = (3×3)/(2×4) = 9/8 = 1 1/8 meters
Fraction Multiplication Quiz
Test your fraction multiplication skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about multiplying fractions:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They had a special system where all fractions were written as sums of unit fractions (fractions with 1 as numerator).
Fractions in Music
Musical rhythms are based on fractions! A whole note lasts 4 beats, a half note lasts 2 beats, a quarter note lasts 1 beat, and so on. Musicians use fractions to read and write music.
Fractions in Space
NASA scientists use fractions to calculate rocket trajectories. A tiny fraction mistake caused the loss of the Mars Climate Orbiter in 1999 - one team used metric units while another used imperial!
Largest Fraction
The fraction with the largest denominator ever used in a published mathematical proof has more than 20 million digits! Most fractions we use in daily life have denominators less than 100.





