Improper Fraction to Mixed Number - Definition, Examples, Quiz, FAQ, Trivia
Learn to convert between different fraction forms with easy explanations and practice activities
What is an Improper Fraction?

Fractions represent parts of a whole. An improper fraction is a fraction where the numerator (top number) is equal to or greater than the denominator (bottom number).
For example, 54 is an improper fraction because 5 (numerator) is greater than 4 (denominator).
A mixed number combines a whole number and a proper fraction. For example, 114 is a mixed number that means "one whole plus one quarter."
Converting between improper fractions and mixed numbers helps us understand and compare different quantities more easily.
Key Concept
Improper fractions have numerators equal to or larger than denominators. Mixed numbers combine whole numbers with proper fractions.
How to Convert Improper Fractions to Mixed Numbers

Converting improper fractions to mixed numbers follows a simple process:
This gives you a whole number (quotient) and a remainder
Of your mixed number
Of the fractional part
As in the original improper fraction
Conversion Formula
To convert any improper fraction to a mixed number, divide the numerator by the denominator.
Remember
Always simplify the fractional part of your mixed number if possible after conversion.
Conversion Examples
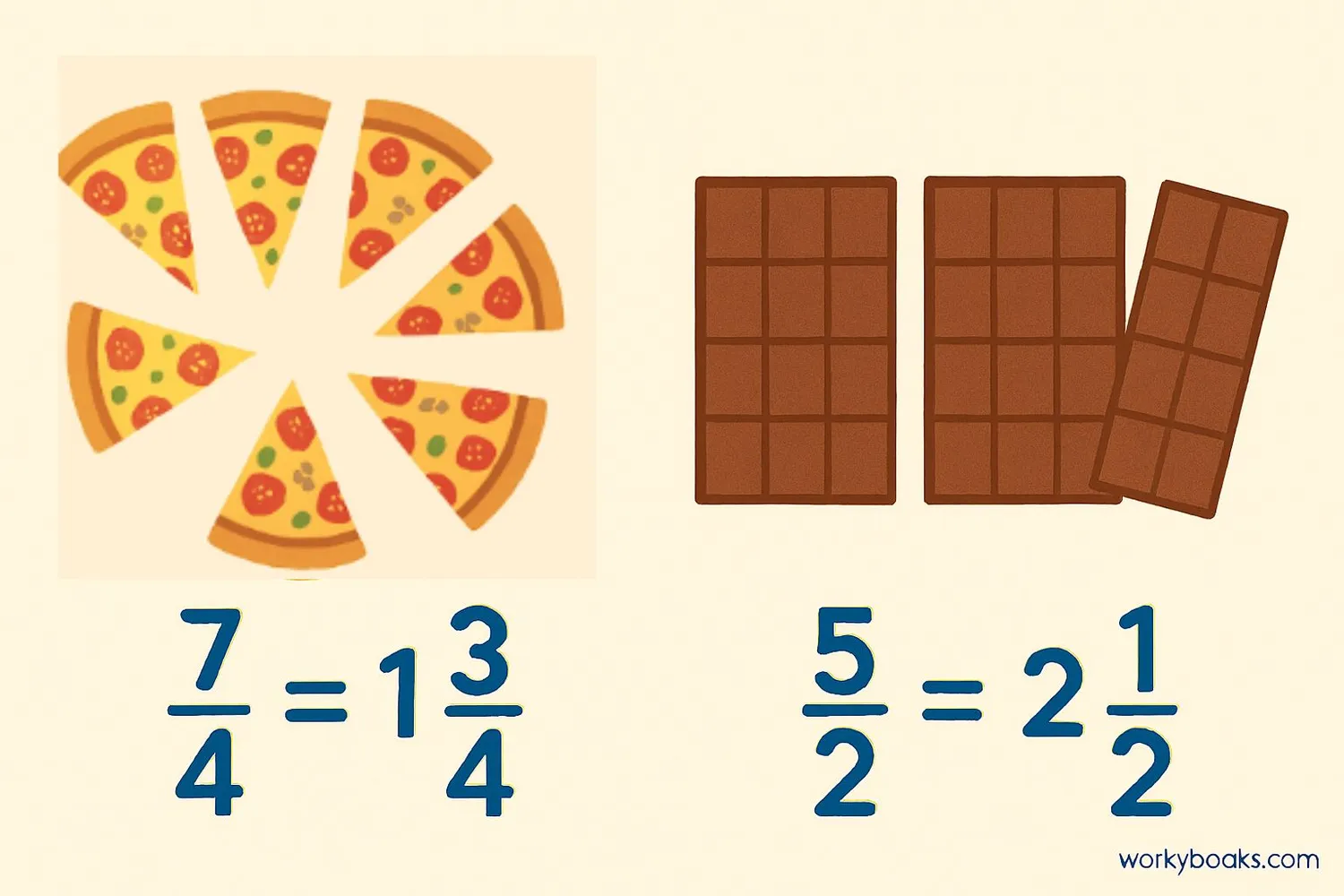
Let's practice conversion with some examples:
Example 1: Convert 74 to a mixed number
Step 1: Divide 7 by 4 → 7 ÷ 4 = 1 with remainder 3
Step 2: Whole number is 1
Step 3: Fraction is 34
Solution: 134
Example 2: Convert 113 to a mixed number
Step 1: Divide 11 by 3 → 11 ÷ 3 = 3 with remainder 2
Step 2: Whole number is 3
Step 3: Fraction is 23
Solution: 323
Example 3: Convert 82 to a mixed number
Step 1: Divide 8 by 2 → 8 ÷ 2 = 4 with remainder 0
Step 2: Whole number is 4
Step 3: When remainder is 0, the mixed number is just the whole number
Solution: 4
Practice converting fractions you encounter in daily life - recipes, measurements, or sharing items with friends!
Conversion Reference Table
| Improper Fraction | Mixed Number |
|---|---|
| 52 | 212 |
| 73 | 213 |
| 94 | 214 |
| 115 | 215 |
| 136 | 216 |
| 157 | 217 |
| 103 | 313 |
Conversion Tip
When the remainder is 0, the mixed number is simply a whole number. When the numerator and denominator are the same, the value equals 1.
Conversion Practice Quiz
Test your conversion skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about improper fractions and mixed numbers:
Fraction Trivia
Discover interesting facts about fractions and their history:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they mainly used unit fractions (fractions with 1 as the numerator). They would write other fractions as sums of unit fractions.
Fraction Word Origin
The word "fraction" comes from the Latin word "fractus" which means "broken." This makes sense because fractions represent broken or divided parts of a whole.
Fractions in Music
Musical notes are based on fractions! A whole note can be divided into half notes, quarter notes, eighth notes, and so on. The time signature in sheet music is actually a fraction.
Fractions in Measurement
Before the metric system, most measurement systems used fractions. The imperial system (still used in the US) commonly uses fractions like 1/2, 1/4, and 1/8 inches for precise measurements.


