Improper Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn about fractions where the numerator is bigger than the denominator with visual examples and practice activities
What are Improper Fractions?

An improper fraction is a fraction where the numerator (top number) is greater than or equal to the denominator (bottom number). This means the fraction represents a value that is equal to or greater than 1 whole.
For example:
Numerator (3) > Denominator (2)
Numerator (2) < Denominator (3)
Whole number + proper fraction
Key Concept
Improper fractions have numerators equal to or larger than their denominators. They represent values that are greater than or equal to one whole.
Converting to Mixed Numbers

We can convert improper fractions to mixed numbers (a whole number plus a proper fraction). Here's how:
Conversion Steps
1. Divide the numerator by the denominator
2. The quotient becomes the whole number
3. The remainder becomes the new numerator
4. Keep the same denominator
- Divide 7 by 4: 7 ÷ 4 = 1 with a remainder of 3
- The quotient (1) becomes the whole number
- The remainder (3) becomes the new numerator
- The denominator stays 4
- So 7/4 = 1¾
Conversion Chart
| Improper Fraction | Mixed Number | Decimal |
|---|---|---|
| 5/2 | 2½ | 2.5 |
| 7/3 | 2⅓ | 2.333 |
| 9/4 | 2¼ | 2.25 |
| 11/5 | 2⅕ | 2.2 |
| 13/6 | 2⅙ | 2.166 |
| 15/7 | 2¹⁄₇ | 2.142 |
Remember
Mixed numbers are often easier to understand in real-world situations like measuring ingredients or describing lengths.
Operations with Improper Fractions
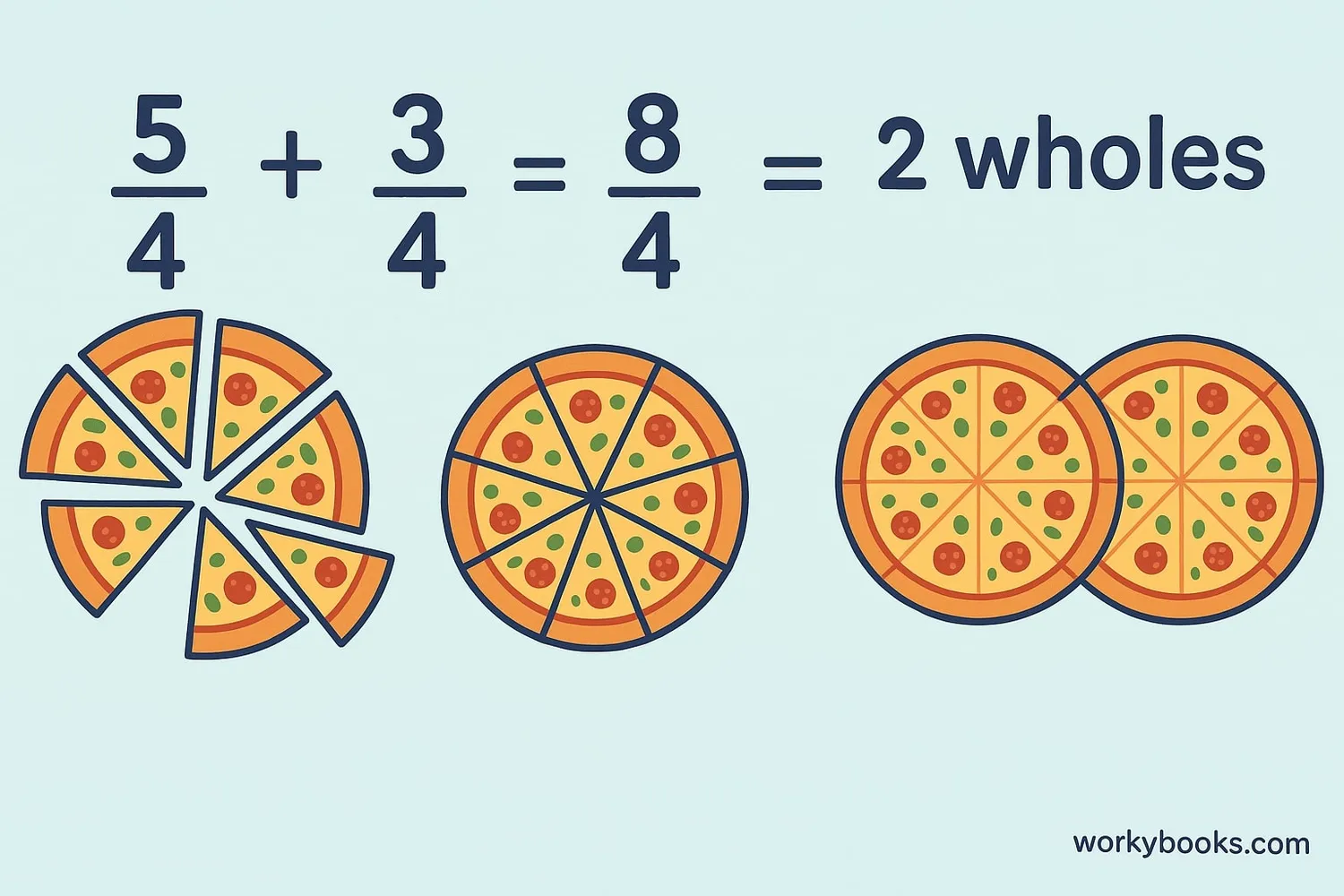
We can add, subtract, multiply, and divide improper fractions just like proper fractions. Here's how:
Adding Improper Fractions
- Make sure denominators are the same
- Add the numerators
- Keep the same denominator
- Simplify if possible
Subtracting Improper Fractions
- Make sure denominators are the same
- Subtract the numerators
- Keep the same denominator
- Simplify if possible
Multiplying Improper Fractions
- Multiply numerators together
- Multiply denominators together
- Simplify the result
Simplifying Fractions
- Find the greatest common factor (GCF) of numerator and denominator
- Divide both numerator and denominator by the GCF
Tip
When working with improper fractions, it's often helpful to convert them to mixed numbers before solving word problems.
Real-World Examples

Let's see how improper fractions appear in everyday situations:
Example 1: Sarah baked cookies and used 5/4 cups of sugar. How much is this as a mixed number?
Solution: 5 ÷ 4 = 1 with remainder 1 → 1¼ cups
Example 2: A carpenter needs 7/2 meters of wood for a project. Convert this to a mixed number.
Solution: 7 ÷ 2 = 3 with remainder 1 → 3½ meters
Example 3: Add 3/2 hours + 5/4 hours of study time. Express as a mixed number.
Solution: First make denominators same: 3/2 = 6/4, then 6/4 + 5/4 = 11/4 = 2¾ hours
Example 4: Multiply 5/3 × 3/2 to find the area of a rectangle.
Solution: 5/3 × 3/2 = 15/6 = 5/2 = 2½ square units
Practice Tip
Look for fractions in recipes, measurements, and time calculations to practice converting between improper fractions and mixed numbers.
Improper Fractions Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about improper fractions:
Fraction Trivia
Discover interesting facts about fractions and mathematics:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they only used unit fractions (fractions with 1 as the numerator). They expressed other fractions as sums of unit fractions.
Fractions in Nature
Fractions appear throughout nature! Beehives have hexagonal cells that can be described using fractions, and the spirals in pinecones and sunflowers follow patterns based on fractions like 1/2, 1/3, 2/5, 3/8, and 5/13.
Fractions in Space
Astronomers use fractions to describe planetary orbits. For example, Mercury orbits the Sun in about 3/8 of an Earth year, while Venus orbits in about 4/7 of an Earth year.
Largest Denominator
The fraction with the largest denominator ever used in a practical application might be in quantum physics, where physicists work with fractions having denominators in the billions!





