Integers - Definition, Examples, Quiz, FAQ, Trivia
Learn about positive and negative numbers with easy explanations and practice activities
What are Integers?
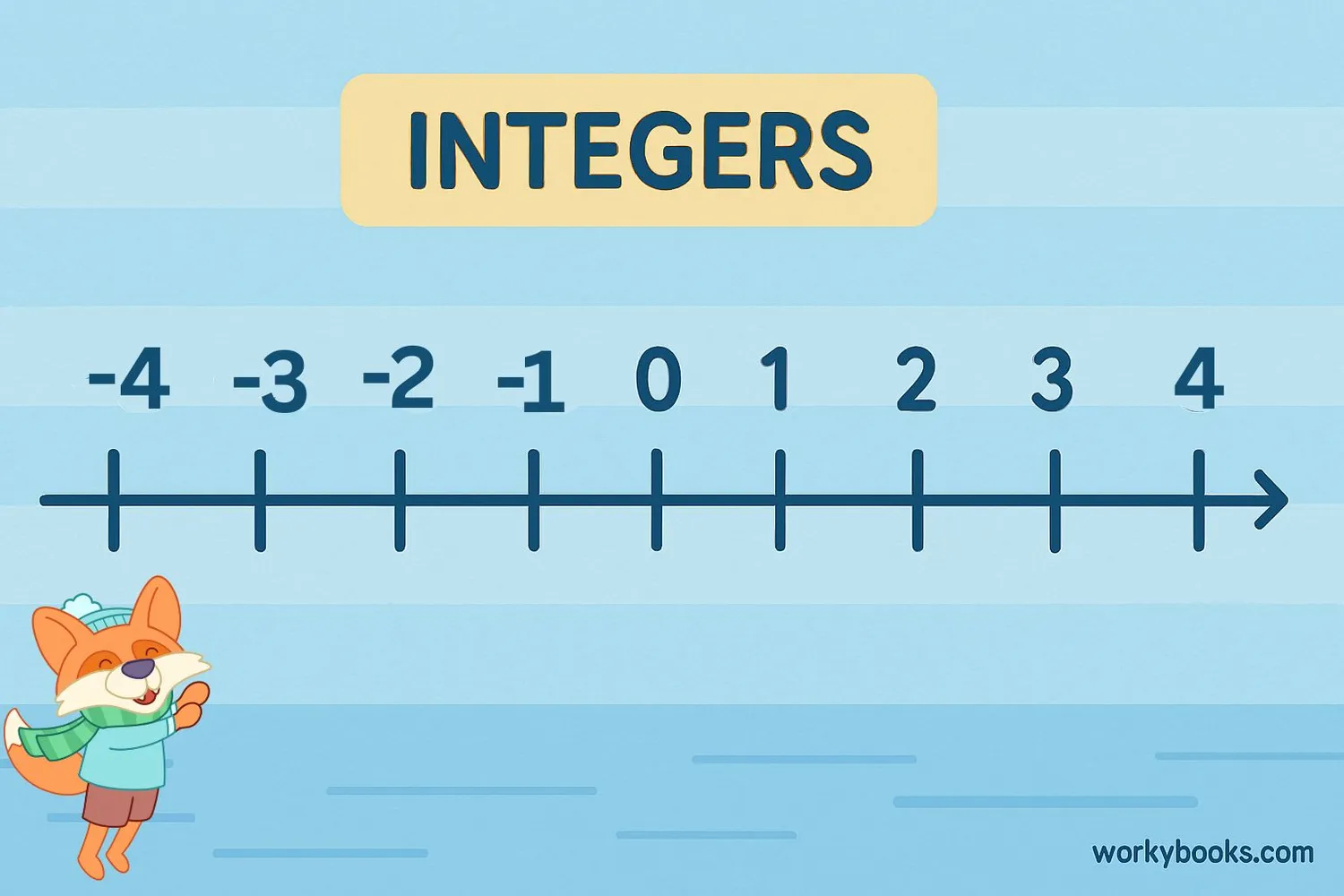
Integers are whole numbers that can be positive, negative, or zero. They do not include fractions or decimals. The set of integers includes all the counting numbers (1, 2, 3, ...), their negatives (-1, -2, -3, ...), and zero (0).
Integers are used in many real-life situations. Positive integers represent gains, increases, or above-zero measurements. Negative integers represent losses, decreases, or below-zero measurements. Zero represents a neutral point or starting position.
The integer number line extends infinitely in both positive and negative directions, with zero at the center. Understanding integers helps us describe situations that have both increase and decrease, like temperature changes, financial gains and losses, or elevation above and below sea level.
Key Concept
Integers are the set of whole numbers and their negatives: {..., -3, -2, -1, 0, 1, 2, 3, ...}.
Positive and Negative Integers
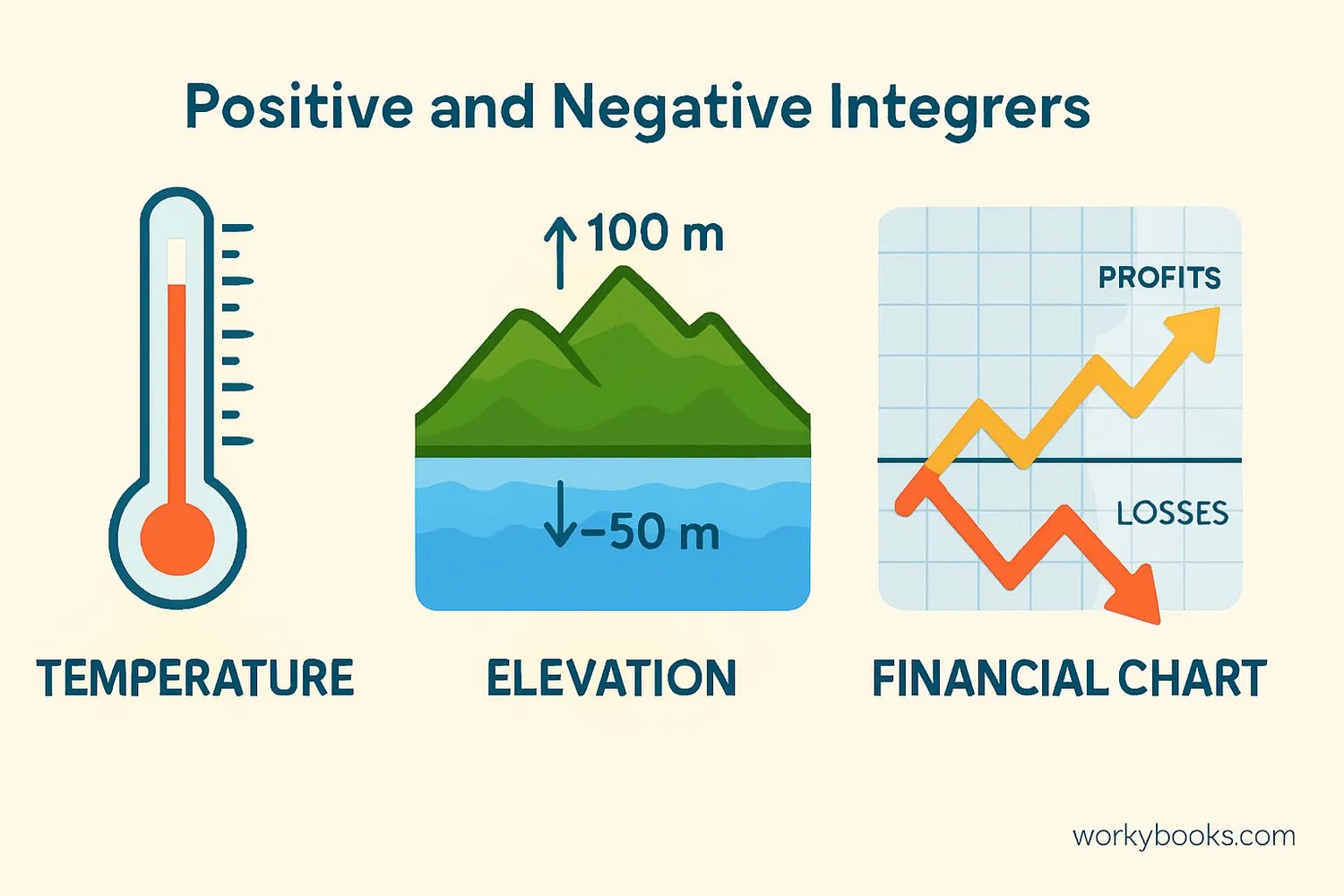
Positive integers are numbers greater than zero. They represent values that are more than nothing, such as:
- A temperature of 25°C (warm day)
- Earning $50 (money gained)
- 300 feet above sea level (mountain)
Negative integers are numbers less than zero. They represent values that are less than nothing, such as:
- A temperature of -10°C (cold day)
- Owing $75 (money owed)
- 50 feet below sea level (valley)
Zero is neither positive nor negative. It represents a neutral point or starting position.
On a number line, positive integers are to the right of zero, and negative integers are to the left of zero. The further right a number is, the greater its value. The further left a number is, the lesser its value.
Remember
Negative numbers are always less than positive numbers. For example, -100 is less than 1, even though 100 is greater than 1 when we ignore the sign.
Integer Operations and Rules
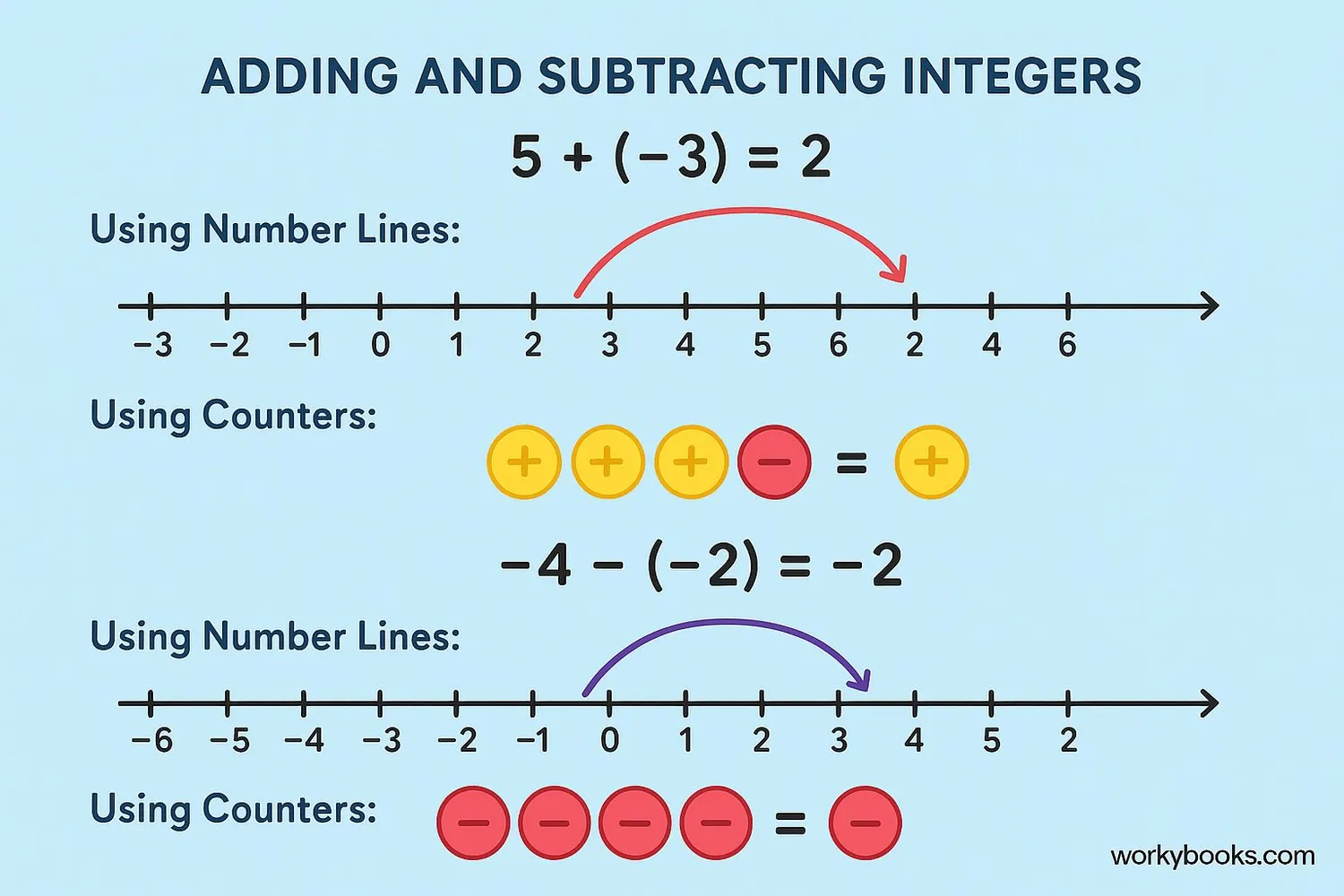
Working with integers follows specific rules. Here are the basic rules for integer operations:
Adding Integers:
- Same signs: Add the numbers and keep the sign
- Different signs: Subtract the smaller number from the larger number and keep the sign of the larger number
Subtracting Integers:
- Change the subtraction sign to addition and change the sign of the number being subtracted, then follow addition rules
Multiplying and Dividing Integers:
- Same signs: Positive result
- Different signs: Negative result
These rules help us solve problems with integers correctly. Let's look at some examples in the next section.
Integer Rules Summary
Integer Examples

Let's look at some examples of integers in action:
Example 1: Temperature
If it's 5°C outside and the temperature drops 8 degrees, what is the new temperature?
Solution: 5 - 8 = -3°C
Example 2: Money
Sarah has $50 in her account. She writes a check for $75. What is her new balance?
Solution: 50 - 75 = -$25 (she owes $25)
Example 3: Elevation
Death Valley is 282 feet below sea level. Mount Whitney is 14,505 feet above sea level. What is the difference in their elevations?
Solution: 14,505 - (-282) = 14,505 + 282 = 14,787 feet
Example 4: Football
A team gains 5 yards, then loses 8 yards, then gains 12 yards. What is their total yardage?
Solution: 5 + (-8) + 12 = (5 + 12) + (-8) = 17 - 8 = 9 yards
These examples show how integers help us solve real-world problems involving increases and decreases.
Practice Tip
When working with integer word problems, identify whether each number represents a positive or negative value based on the context.
Integer Practice Quiz
Test your understanding of integers with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about integers:
Math Trivia
Discover interesting facts about integers and numbers:
Historical Acceptance
Negative numbers were not widely accepted in European mathematics until the 17th century, though they had been used in Chinese mathematics as early as 200 BCE.
Integer in Computing
In computer programming, integers are a fundamental data type. Computers represent integers using binary code (0s and 1s), with special methods to handle negative numbers.
Infinite in Both Directions
The set of integers is infinite in both positive and negative directions. No matter how large a positive integer you name, there's always a larger one, and similarly for negative integers.
Prime Numbers
Prime numbers are positive integers greater than 1 that have no positive divisors other than 1 and themselves. The largest known prime number has over 24 million digits!





