Interior Angles - Definition, Examples, Quiz, FAQ, Trivia
Learn about angles inside polygons with easy explanations and interactive activities
What are Interior Angles?
Interior angles are the angles inside a shape. When we have a polygon (a closed shape with straight sides), the angles on the inside where two sides meet are called interior angles.
Every polygon has the same number of interior angles as it has sides. A triangle has 3 interior angles, a quadrilateral has 4 interior angles, and a pentagon has 5 interior angles.
The sum of all interior angles in a polygon depends on how many sides it has. As the number of sides increases, the sum of the interior angles also increases.
Key Concept
Interior angles are the angles inside a polygon where two sides meet. Every polygon has as many interior angles as it has sides.
Interior Angles of a Triangle
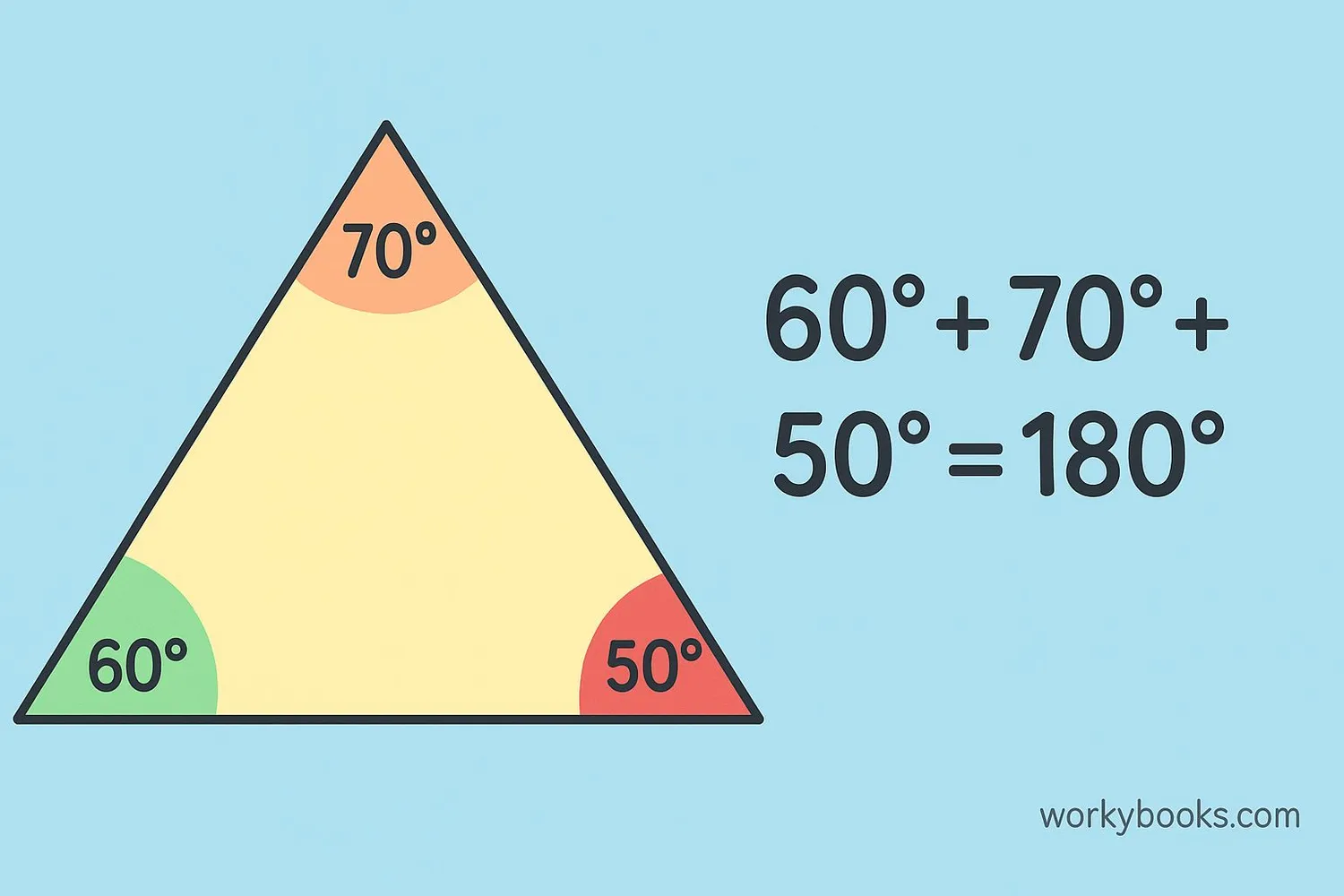
A triangle is a polygon with three sides and three interior angles. No matter what type of triangle you have (equilateral, isosceles, or scalene), the sum of its interior angles is always 180 degrees.
This is a special property of triangles that makes them unique among polygons.
Triangle Angle Sum
The three interior angles of any triangle always add up to 180 degrees.
Remember
All triangles have interior angles that add up to exactly 180 degrees, regardless of the triangle's size or shape.
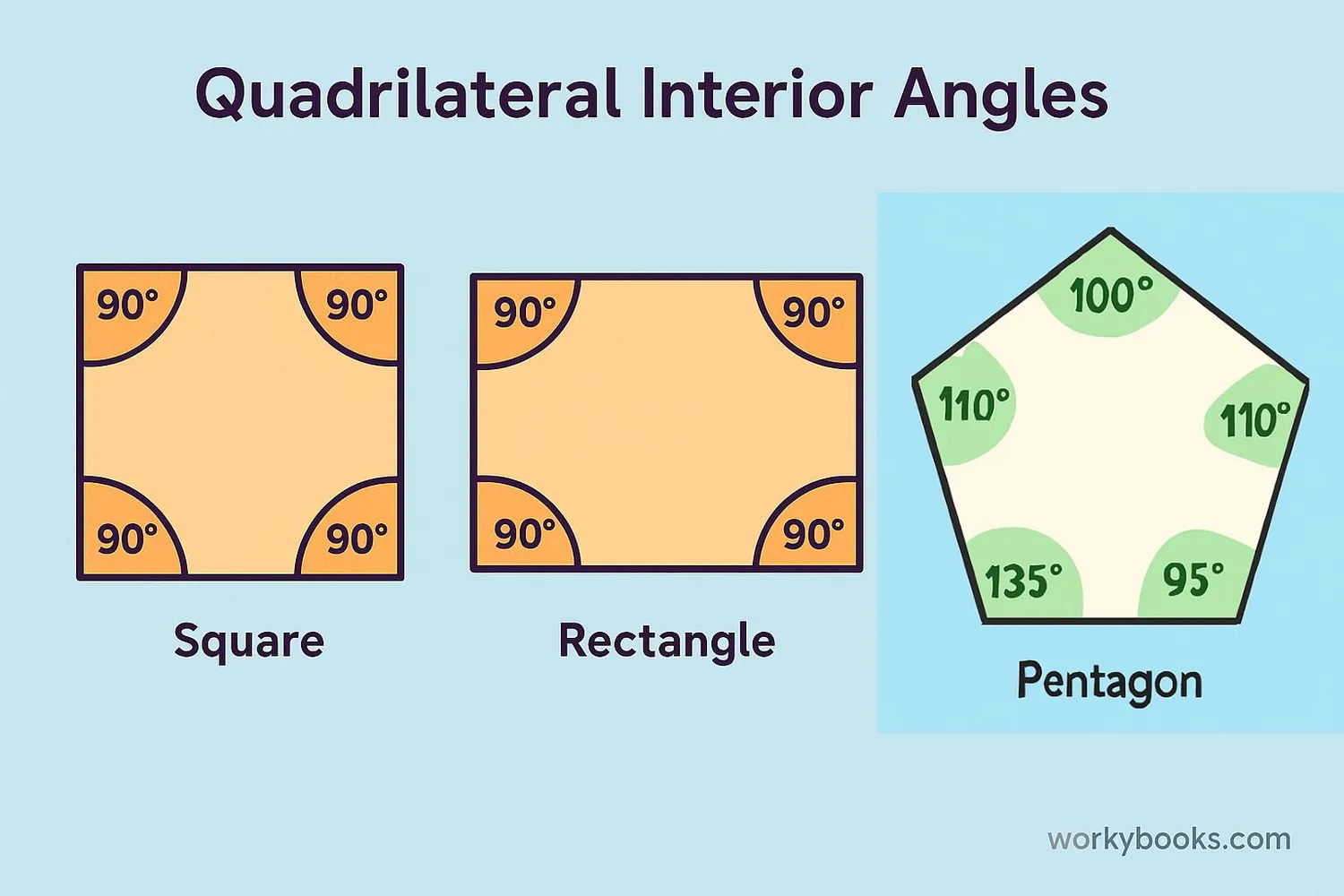
Interior Angles of a Quadrilateral
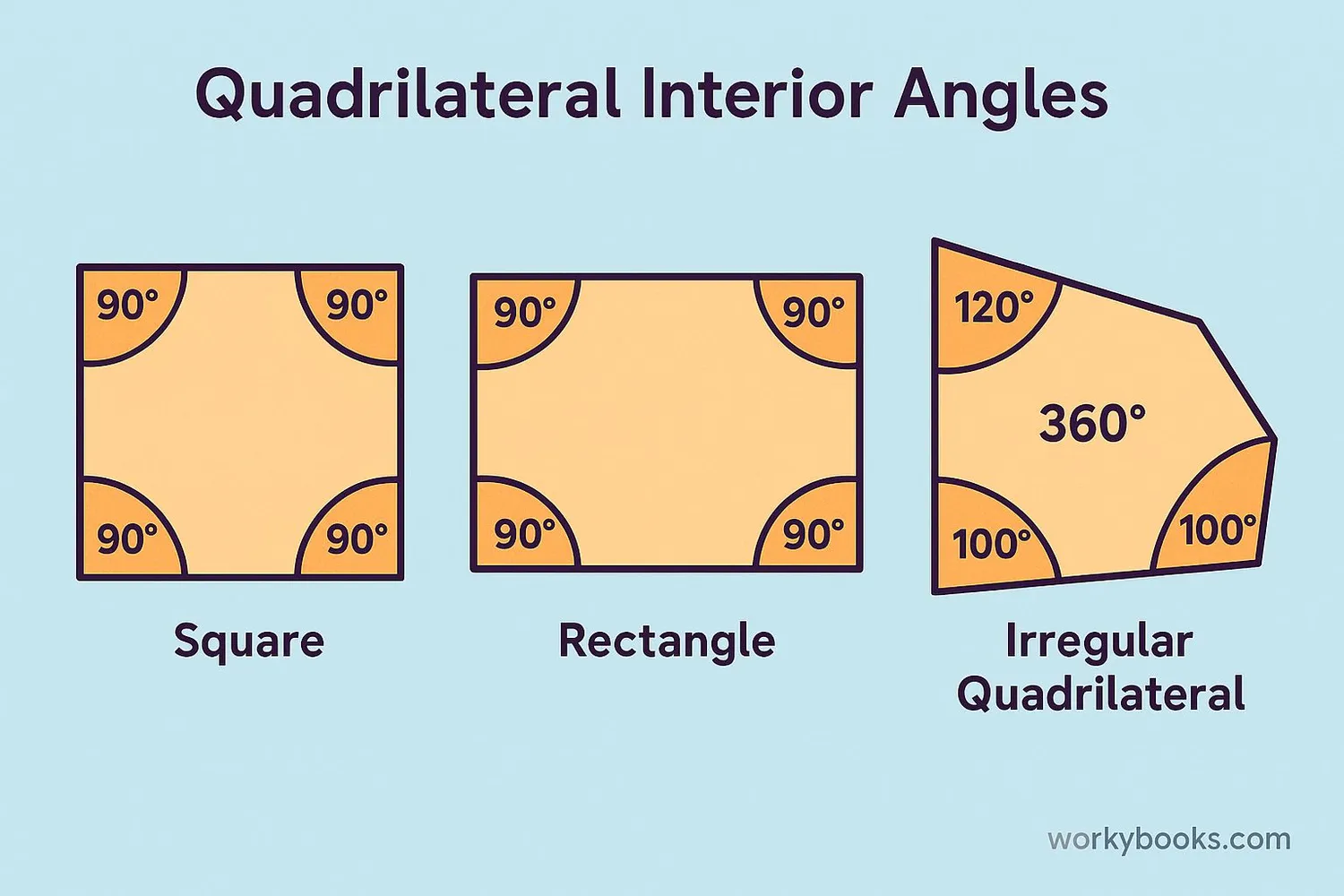
A quadrilateral is a polygon with four sides and four interior angles. Examples of quadrilaterals include squares, rectangles, parallelograms, and trapezoids.
The sum of the interior angles of any quadrilateral is always 360 degrees. This is true regardless of the shape of the quadrilateral.
Quadrilateral Angle Sum
The four interior angles of any quadrilateral always add up to 360 degrees.
Square: 4 × 90° = 360°
Quadrilateral: 100° + 80° + 100° + 80° = 360°
Sum of Interior Angles in Polygons
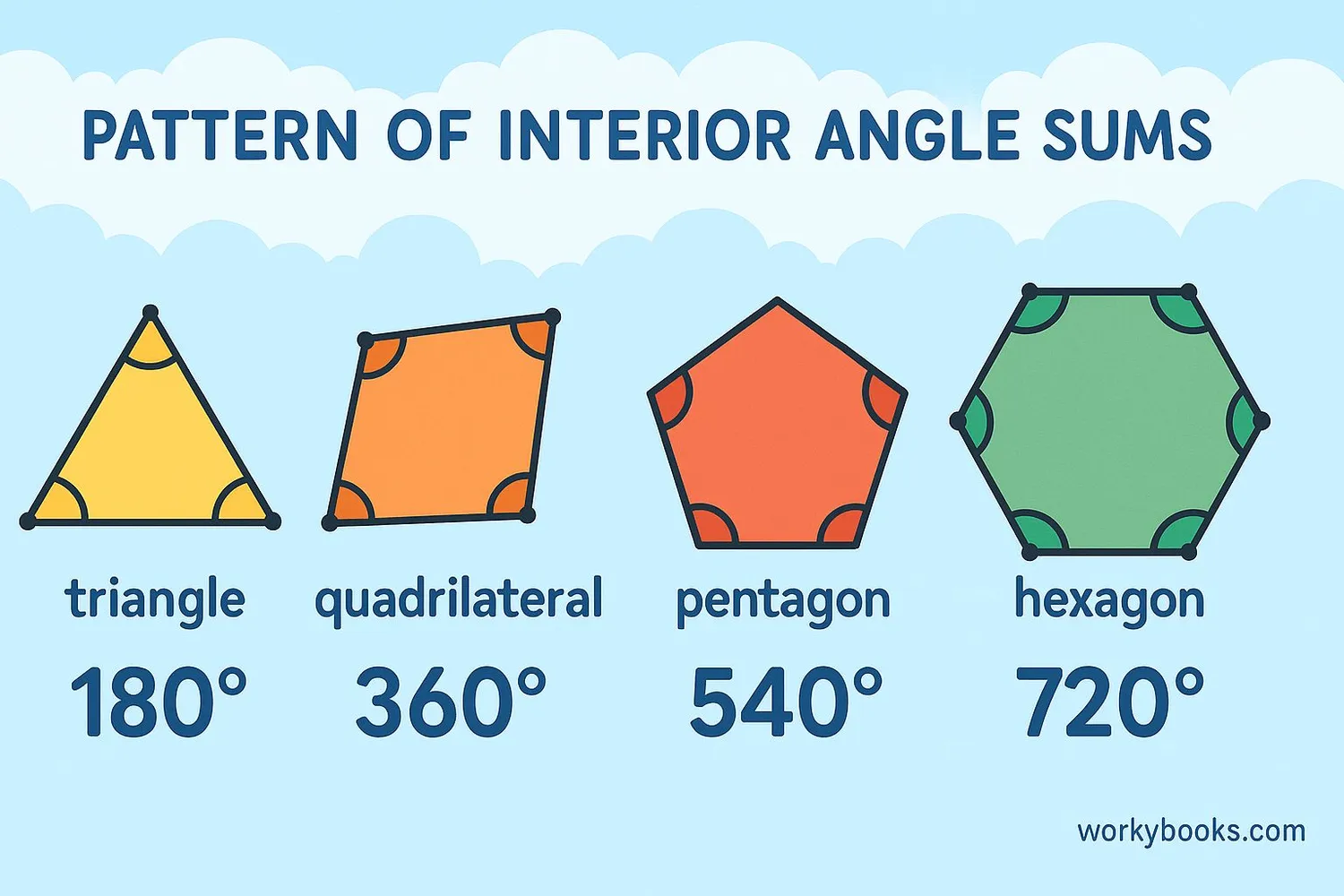
For any polygon, we can calculate the sum of its interior angles using a simple formula. The formula is based on the number of sides the polygon has.
Interior Angle Sum Formula
Where n is the number of sides in the polygon
• Triangle (3 sides): (3 - 2) × 180° = 1 × 180° = 180°
• Quadrilateral (4 sides): (4 - 2) × 180° = 2 × 180° = 360°
• Pentagon (5 sides): (5 - 2) × 180° = 3 × 180° = 540°
• Hexagon (6 sides): (6 - 2) × 180° = 4 × 180° = 720°
This pattern continues for polygons with more sides. The more sides a polygon has, the greater the sum of its interior angles.
Interior Angle Sums for Common Polygons
| Polygon | Number of Sides | Sum of Interior Angles |
|---|---|---|
| Triangle | 3 | 180° |
| Quadrilateral | 4 | 360° |
| Pentagon | 5 | 540° |
| Hexagon | 6 | 720° |
| Heptagon | 7 | 900° |
| Octagon | 8 | 1080° |
| Nonagon | 9 | 1260° |
| Decagon | 10 | 1440° |
Finding Interior Angles
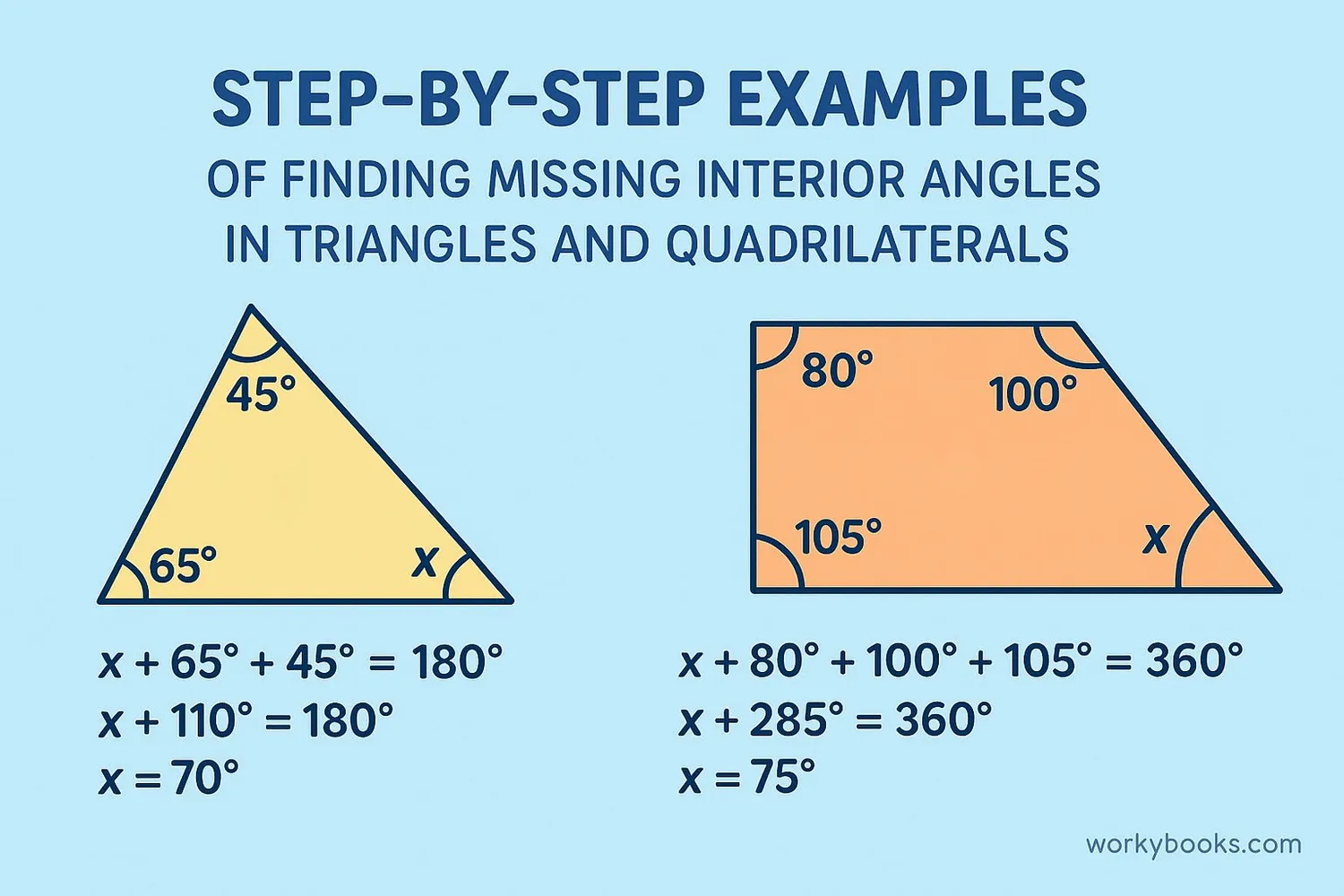
We can use what we know about the sum of interior angles to find missing angles in polygons. Here are some examples:
Example 1: Find the missing angle in a triangle with angles measuring 45° and 60°.
Solution: We know triangles have 180° total, so: 180° - 45° - 60° = 75°
Example 2: Three angles in a quadrilateral measure 80°, 110°, and 90°. Find the fourth angle.
Solution: Quadrilaterals have 360° total, so: 360° - 80° - 110° - 90° = 80°
Example 3: A regular pentagon has equal angles. What is the measure of each interior angle?
Solution: First find the total: (5 - 2) × 180° = 540°. Then divide by 5: 540° ÷ 5 = 108°
For regular polygons (where all sides and angles are equal), we can find each interior angle by dividing the sum of interior angles by the number of angles.
Practice Tip
Remember the sum for each type of polygon, then subtract the known angles to find any missing angle.
Interior Angles Practice Quiz
Test your knowledge about interior angles with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about interior angles:
Geometry Trivia
Discover interesting facts about geometry and angles:
Ancient Geometry
The study of angles and shapes dates back to ancient civilizations. The Egyptians used geometry around 3000 BC to restore field boundaries after the Nile River flooded each year.
Polygon Names
Polygons are named based on their number of sides. "Tri" means 3, "Quad" means 4, "Penta" means 5, "Hexa" means 6, "Hepta" means 7, "Octa" means 8, "Nona" means 9, and "Deca" means 10.
Bees and Hexagons
Honeybees build their hives with hexagonal cells. This shape is efficient because hexagons fit together perfectly without gaps, and they use the least amount of wax to create the most storage space.
Ancient Structures
The Great Pyramid of Giza in Egypt is the oldest of the Seven Wonders of the Ancient World. Its base is almost a perfect square, with the sides aligned to the four cardinal directions with amazing accuracy.


