Irrational Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn about numbers that can't be expressed as simple fractions with easy explanations and practice activities
What Are Irrational Numbers?

Irrational numbers are numbers that cannot be written as a simple fraction of two integers (like 1/2 or 3/4).
Unlike rational numbers, irrational numbers have decimal expansions that go on forever without repeating patterns. This means we can't write them as exact fractions.
The ancient Greeks discovered irrational numbers when they tried to measure the diagonal of a square. They found that no matter how hard they tried, they couldn't express this measurement as a fraction of the side length.
Key Concept
Irrational numbers cannot be expressed as a ratio of two integers. Their decimal representation is non-terminating and non-repeating.
Examples of Irrational Numbers
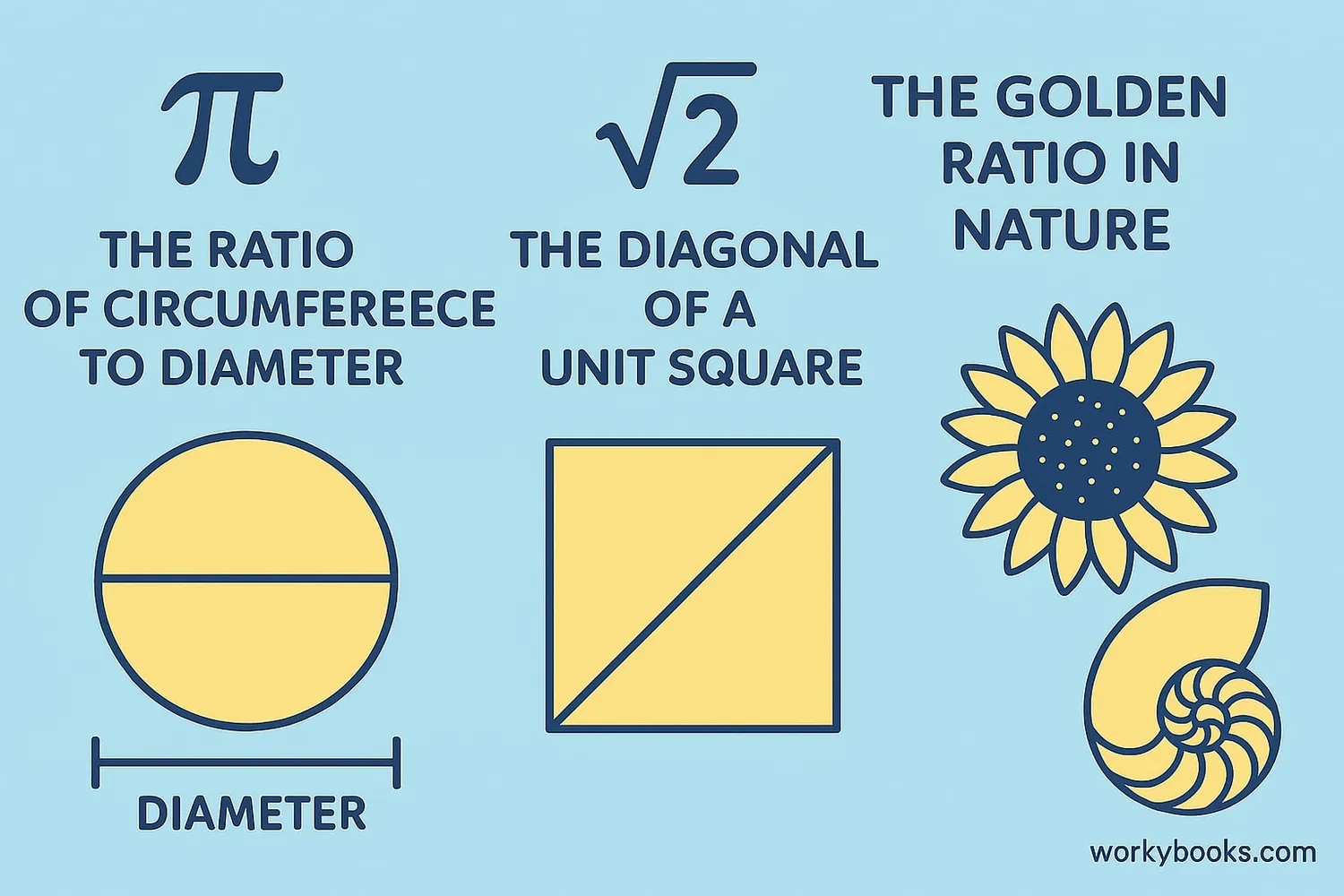
Here are some common examples of irrational numbers:
- π (Pi) ≈ 3.1415926535... - The ratio of a circle's circumference to its diameter
- √2 ≈ 1.4142135623... - The diagonal of a square with sides of length 1
- √3 ≈ 1.7320508075... - The height of an equilateral triangle with sides of length 2
- e ≈ 2.7182818284... - Euler's number, important in calculus and growth problems
- φ (Phi) ≈ 1.6180339887... - The golden ratio, found in art, architecture, and nature
Remember
Not all square roots are irrational! Square roots of perfect squares (like √4, √9, √16) are rational numbers.
Properties of Irrational Numbers

Irrational numbers have some special properties:
Key Properties
- Non-terminating, non-repeating decimals
- Cannot be expressed as fractions of integers
- The sum of a rational and irrational number is irrational
- The product of a non-zero rational and irrational number is irrational
- There are more irrational numbers than rational numbers
These properties help mathematicians work with irrational numbers and understand how they behave in different mathematical operations.
Interesting Fact
Between any two rational numbers, there are infinitely many irrational numbers, and between any two irrational numbers, there are infinitely many rational numbers!
How to Find Irrational Numbers
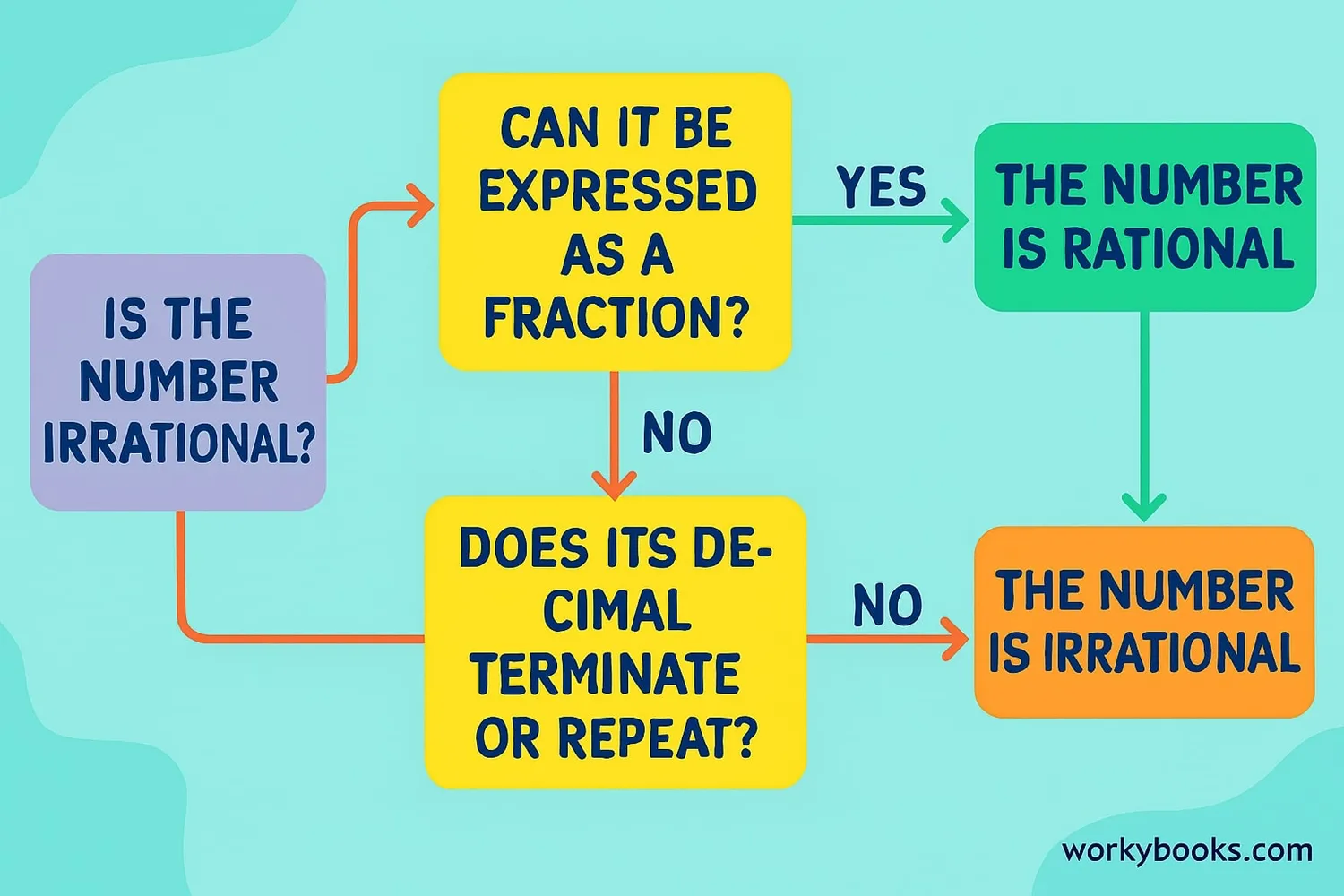
You can identify irrational numbers using these methods:
1. Check if it can be a fraction: If a number cannot be expressed as a fraction of two integers, it's irrational.
2. Look at the decimal: If the decimal goes on forever without repeating, it's irrational.
3. Check square roots: Square roots of numbers that are not perfect squares are usually irrational.
4. Special constants: Numbers like π and e are known to be irrational.
Practice Example
Is 0.12112111211112... rational or irrational?
The pattern changes (one more '1' each time), so it doesn't repeat exactly.
Tip
When in doubt, try to write the number as a fraction. If you can't, it's probably irrational.
Irrational Numbers Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about irrational numbers:
Math Trivia
Discover interesting facts about numbers and mathematics:
Hippasus' Discovery
The Pythagorean Hippasus is credited with discovering irrational numbers around the 5th century BCE. Legend says he was drowned at sea for revealing this disturbing mathematical truth that challenged Pythagorean beliefs.
Calculating Pi
While we know π is irrational, mathematicians continue to calculate its digits. The current record is over 100 trillion digits after the decimal point! Despite this incredible precision, we'll never find the exact value of π.
Different Infinities
There are more irrational numbers than rational numbers! While both are infinite sets, irrational numbers form an "uncountable infinity" which is larger than the "countable infinity" of rational numbers.
Practical Uses
Irrational numbers are essential in many real-world applications, including engineering, physics, computer graphics, and cryptography. GPS systems, for example, rely on calculations involving irrational numbers for accurate positioning.





