Lattice Multiplication - Definition, Examples, Quiz, FAQ, Trivia
Learn the lattice method for multiplication with easy explanations and practice activities
What is Lattice Multiplication?
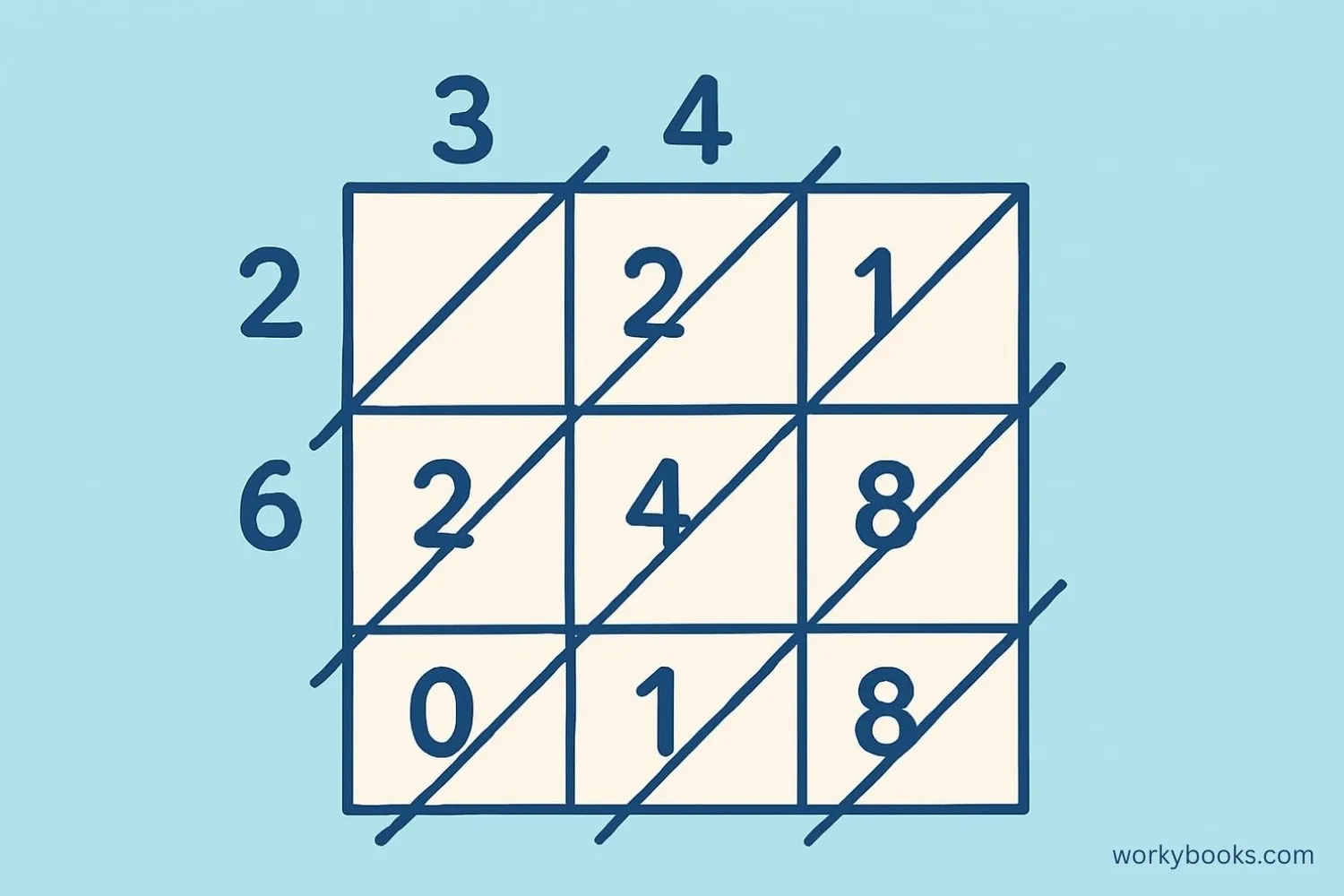
Lattice multiplication is a method for multiplying numbers using a grid. This method breaks down the multiplication process into smaller, easier steps. It's especially helpful when multiplying larger numbers because it organizes the work in a clear, structured way.
The lattice method uses a grid with diagonal lines. Each digit of the numbers being multiplied has its own cell in the grid. This method helps keep track of place values (ones, tens, hundreds) and makes it less likely to make mistakes.
Lattice multiplication has been used for hundreds of years and was popular in medieval times. It's still useful today for visual learners who benefit from seeing the multiplication process step by step.
Key Concept
Lattice multiplication uses a grid to organize the multiplication process, making large number multiplication easier to manage.
How to Do Lattice Multiplication
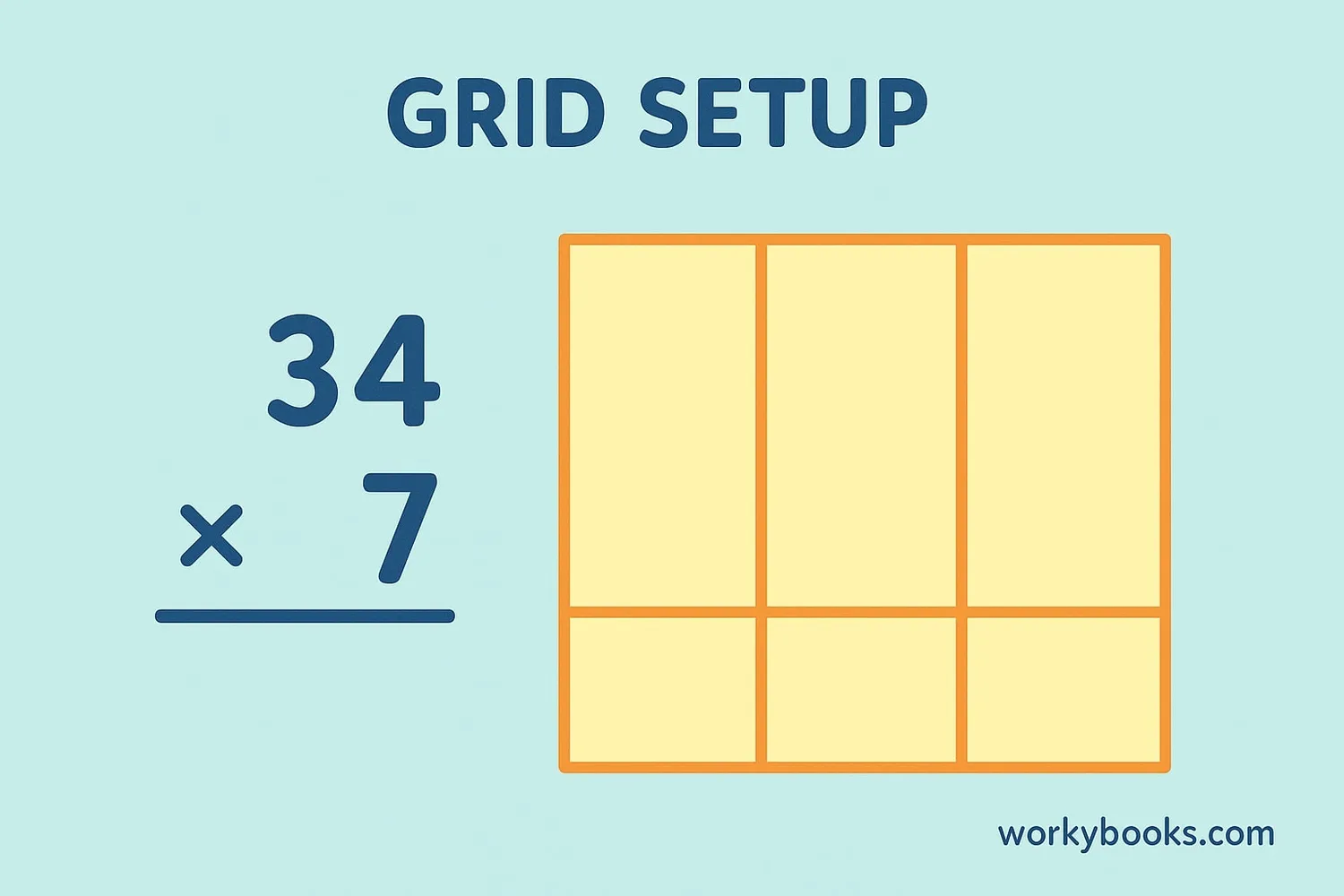
Let's learn how to do lattice multiplication step by step. We'll use the example of multiplying 23 × 45.
Step 1: Draw the Lattice Grid
Draw a grid with rows and columns based on the number of digits in your numbers. For 23 × 45, both numbers have 2 digits, so you need a 2×2 grid. Draw diagonal lines through each cell from top-right to bottom-left.
Step 2: Write the Numbers
Write one number across the top of the grid (one digit per column) and the other number down the right side (one digit per row). For 23 × 45, you would write 2 and 3 across the top, and 4 and 5 down the right side.
Step 3: Multiply and Fill the Cells
Multiply the digit at the top of each column by the digit at the right of each row. Write the product in the corresponding cell, with the tens digit in the top left of the cell and the ones digit in the bottom right.
For example: 2 × 4 = 08 (write 0 in top left, 8 in bottom right)
Step 4: Add Along the Diagonals
Starting from the bottom right corner, add the numbers along each diagonal. If a sum is 10 or more, carry over to the next diagonal.
Step 5: Read the Answer
The final product is read from the top left to the bottom right. In our example, 23 × 45 = 1,035.
Remember
Always write the products with the tens digit in the top left of the cell and the ones digit in the bottom right. This keeps the place values organized.
Lattice Multiplication Examples
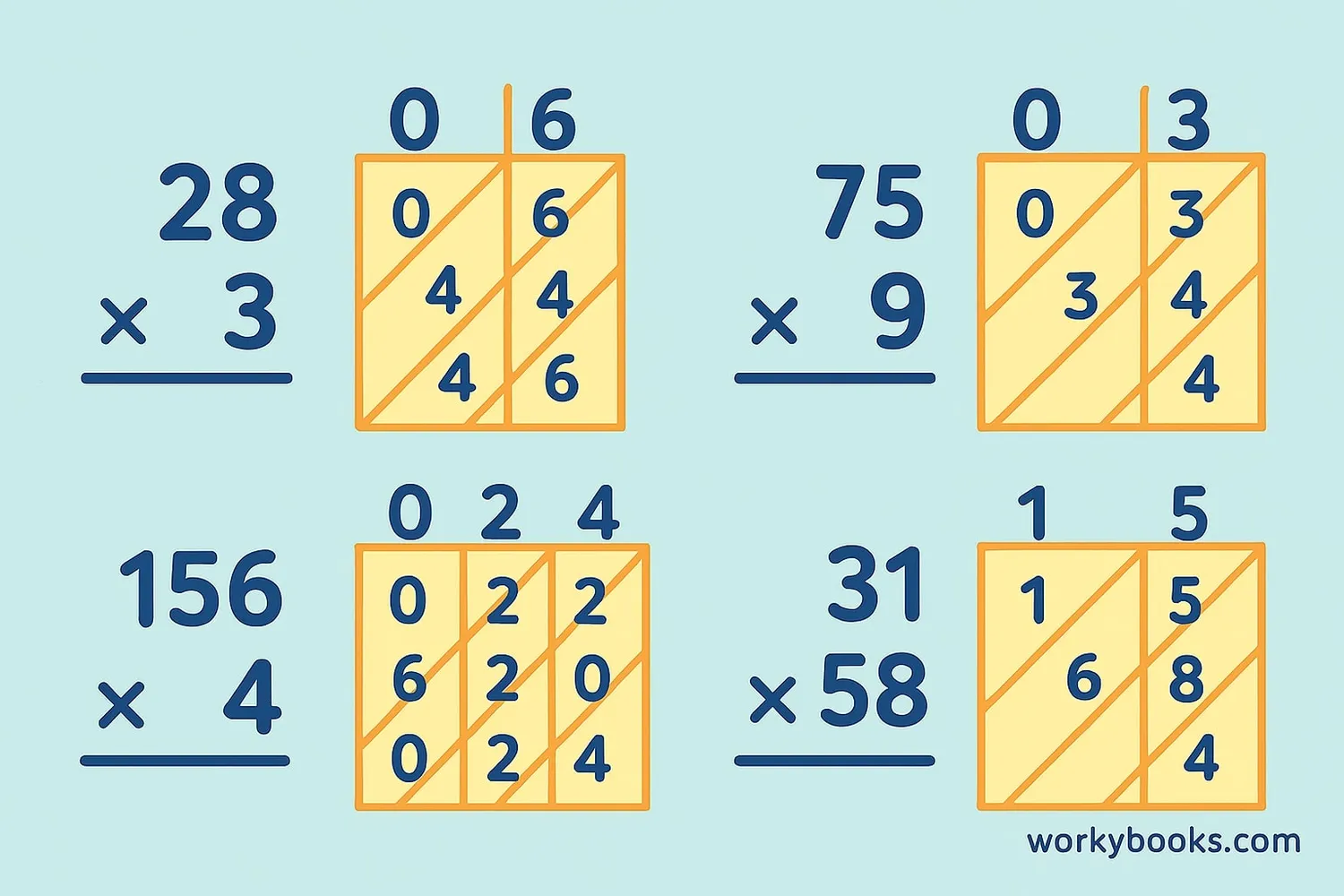
Let's look at some examples of lattice multiplication to better understand how it works:
Example 1: 12 × 34
1. Draw a 2×2 grid
2. Write 1 and 2 across the top, 3 and 4 down the right side
3. Multiply: 1×3 = 03, 1×4 = 04, 2×3 = 06, 2×4 = 08
4. Add diagonals: right diagonal: 8, next: 0+0+6=6, next: 0+0+0=0, left: 0
5. Read answer: 408
Example 2: 56 × 78
1. Draw a 2×2 grid
2. Write 5 and 6 across the top, 7 and 8 down the right side
3. Multiply: 5×7 = 35, 5×8 = 40, 6×7 = 42, 6×8 = 48
4. Add diagonals: right: 8, next: 4+4+0=8 (carry 0), next: 3+4+2+0=9, left: 4
5. Read answer: 4,368
Example 3: 123 × 45 (3-digit × 2-digit)
1. Draw a 3×2 grid
2. Write 1, 2, 3 across the top, 4 and 5 down the right side
3. Multiply each pair of digits
4. Add along the diagonals
5. Read answer: 5,535
Practice Tip
Start with smaller numbers and gradually work your way up to larger multiplication problems. Practice helps you become faster and more accurate.
Lattice Multiplication Quiz
Test your understanding of lattice multiplication with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about lattice multiplication:
Math Trivia
Discover interesting facts about multiplication and mathematics:
Ancient Multiplication
The earliest evidence of multiplication comes from ancient Egypt around 2000 BC. Egyptians used a method called doubling to multiply numbers, which is similar to modern binary multiplication.
Multiplication Symbol
The multiplication sign (×) was introduced by mathematician William Oughtred in 1631. Before that, mathematicians used the letter M or wrote out "multiplied by."
Largest Multiplication
The largest multiplication problem ever solved involved numbers with over 13 million digits each! It took hundreds of computers working together to calculate the product.
Multiplication in Nature
Many patterns in nature follow multiplication rules. For example, the number of petals on flowers often follows the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13...), where each number is the sum of the two before it.





