Like Fractions and Unlike Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn to identify, compare, and work with fractions that have the same and different denominators
What are Fractions?
Fractions represent parts of a whole. They have two numbers:
Numerator (top number) - tells how many parts we have
Denominator (bottom number) - tells how many equal parts the whole is divided into
For example, in the fraction ¾:
- The denominator is 4, which means the whole is divided into 4 equal parts
- The numerator is 3, which means we have 3 of those parts
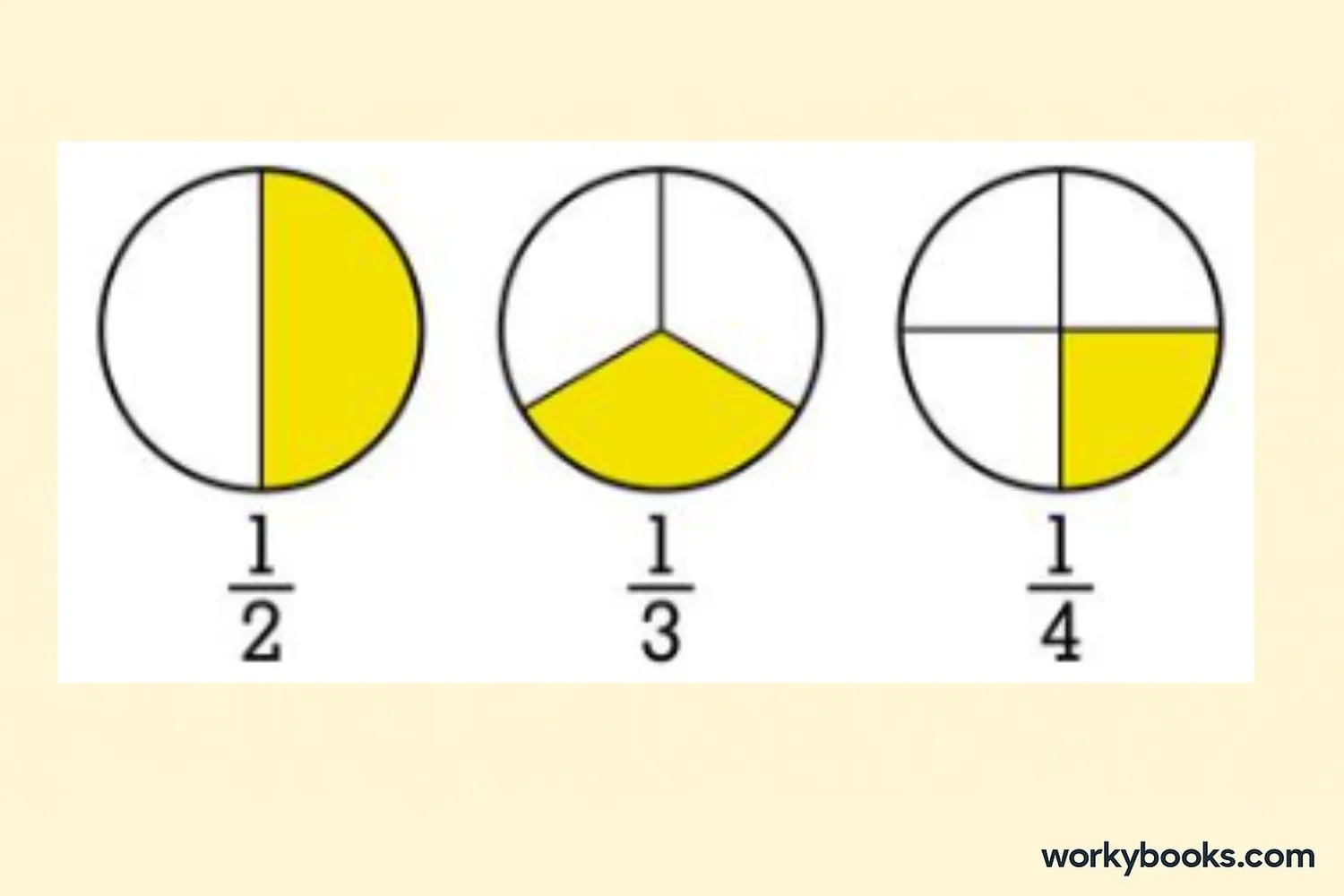
One half
One third
One quarter
Key Concept
A fraction represents equal parts of a whole. The denominator shows how many parts make a whole, and the numerator shows how many of those parts we have.
What are Like Fractions?
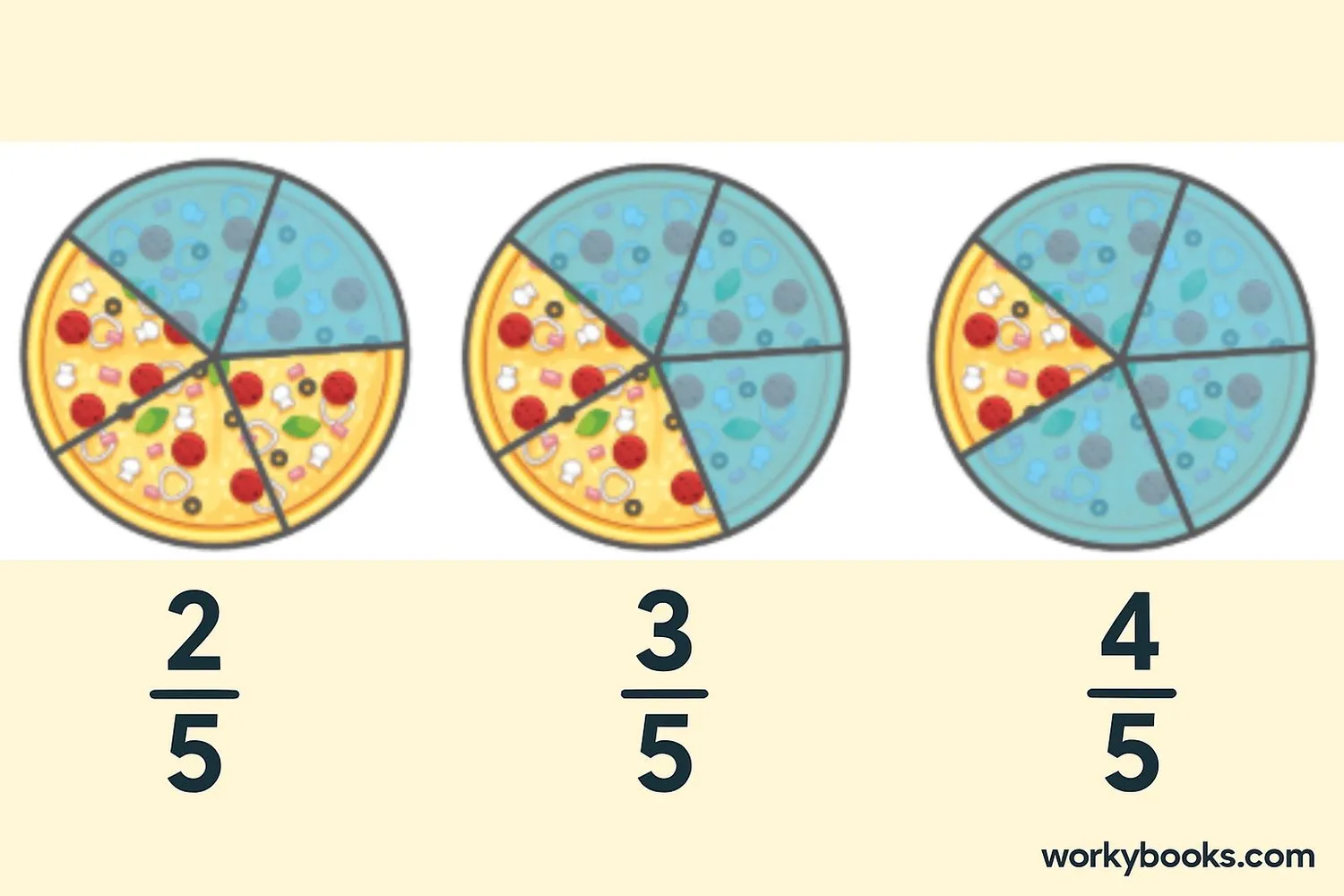
Like fractions are fractions that have the same denominator.
Examples of like fractions:
• ¼, ¾, and ¼ (all have denominator 4)
• ⅕, ⅗, and ⅘ (all have denominator 5)
• ²⁄₇, ⁴⁄₇, and ⁶⁄₇ (all have denominator 7)
Since like fractions have the same denominator, it means they represent parts of the same size. This makes them easier to compare and combine.
Remember
Like fractions have the same denominator. They represent parts of the same size, which makes them easier to work with.
What are Unlike Fractions?
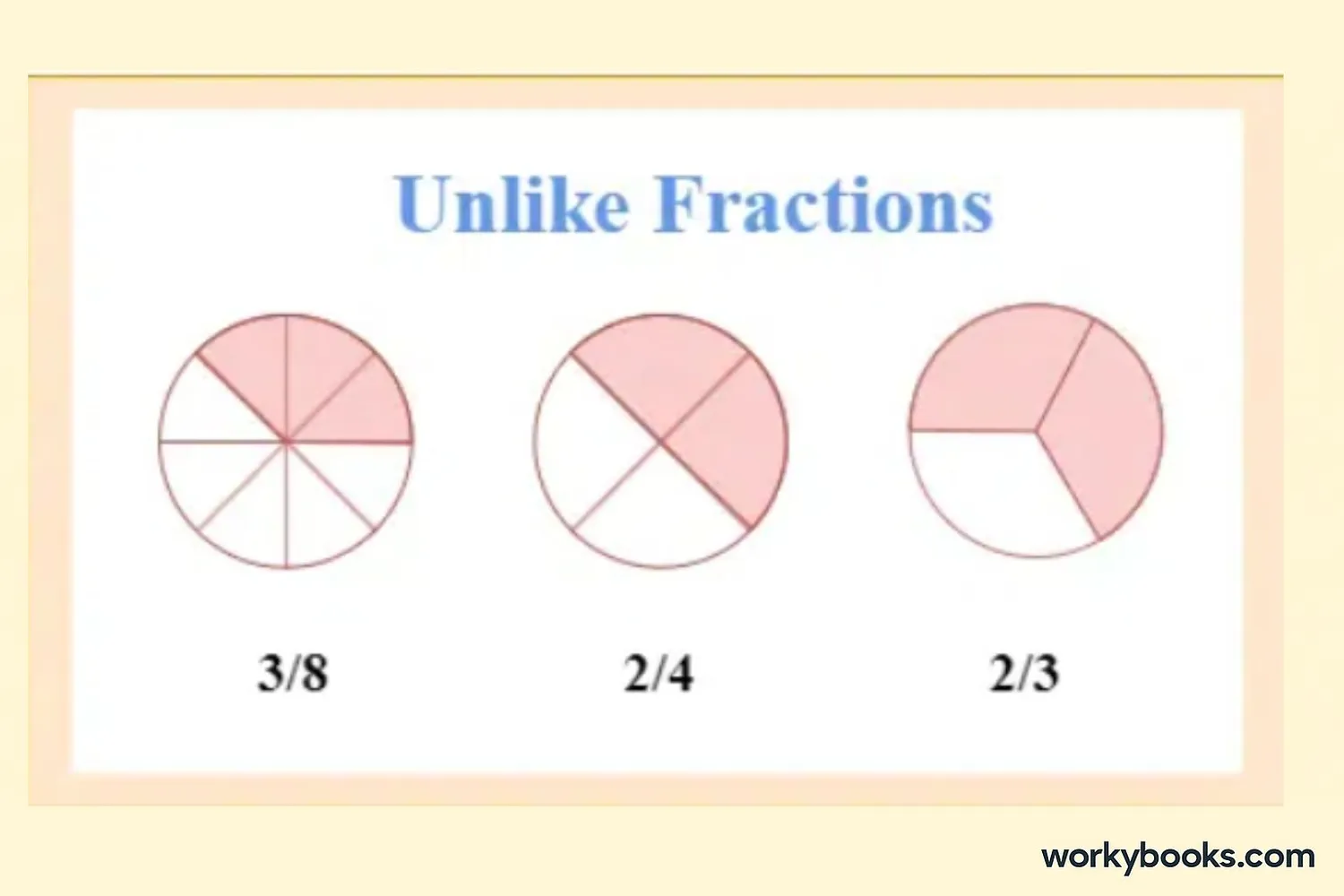
Unlike fractions are fractions that have different denominators.
Examples of unlike fractions:
• ½, ⅓, and ¼ (denominators 2, 3, and 4)
• ²⁄₃, ³⁄₄, and ⅖ (denominators 3, 4, and 5)
• ⅛, ³⁄₁₀, and ⅖ (denominators 8, 10, and 5)
Since unlike fractions have different denominators, they represent parts of different sizes. This makes them more challenging to compare and combine directly.
Remember
Unlike fractions have different denominators. They represent parts of different sizes, so we need to convert them to like fractions before we can add or subtract them.
Converting Unlike Fractions to Like Fractions
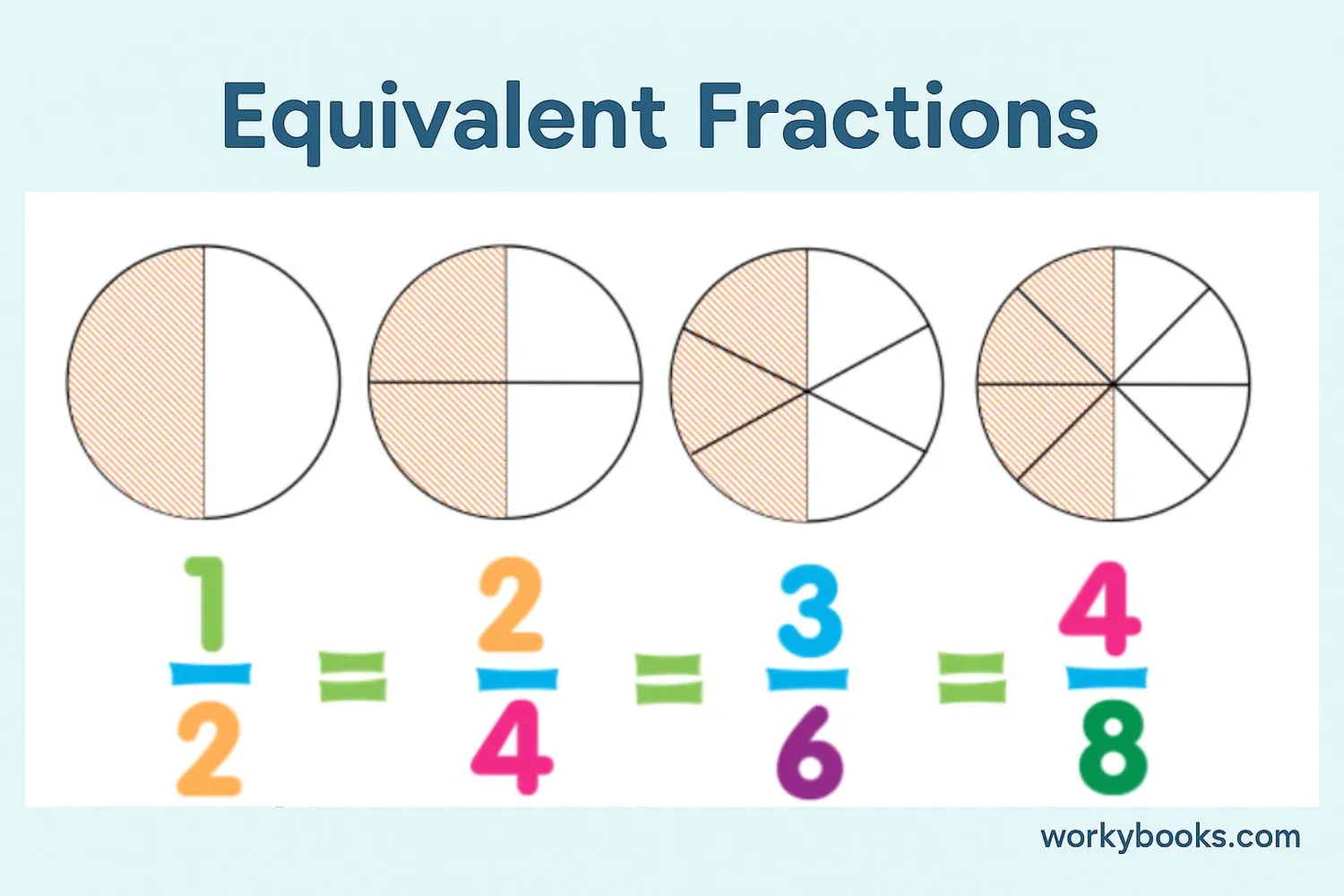
To convert unlike fractions to like fractions, we need to find a common denominator. Here's how:
Step 1: Find the Least Common Multiple (LCM) of the denominators
Step 2: Convert each fraction to an equivalent fraction with the common denominator
Step 3: Now the fractions are like fractions and can be compared or combined
Example: Convert ½ and ⅓ to like fractions
Step 1: LCM of 2 and 3 is 6
Step 2:
• ½ = (1×3)/(2×3) = ³⁄₆
• ⅓ = (1×2)/(3×2) = ²⁄₆
Step 3: Now we have like fractions: ³⁄₆ and ²⁄₆
Conversion Formula
To convert to a common denominator, multiply numerator and denominator by the same number.
Conversion Tip
When converting unlike fractions to like fractions, always multiply both the numerator and denominator by the same number to create equivalent fractions.
Adding and Subtracting Like and Unlike Fractions
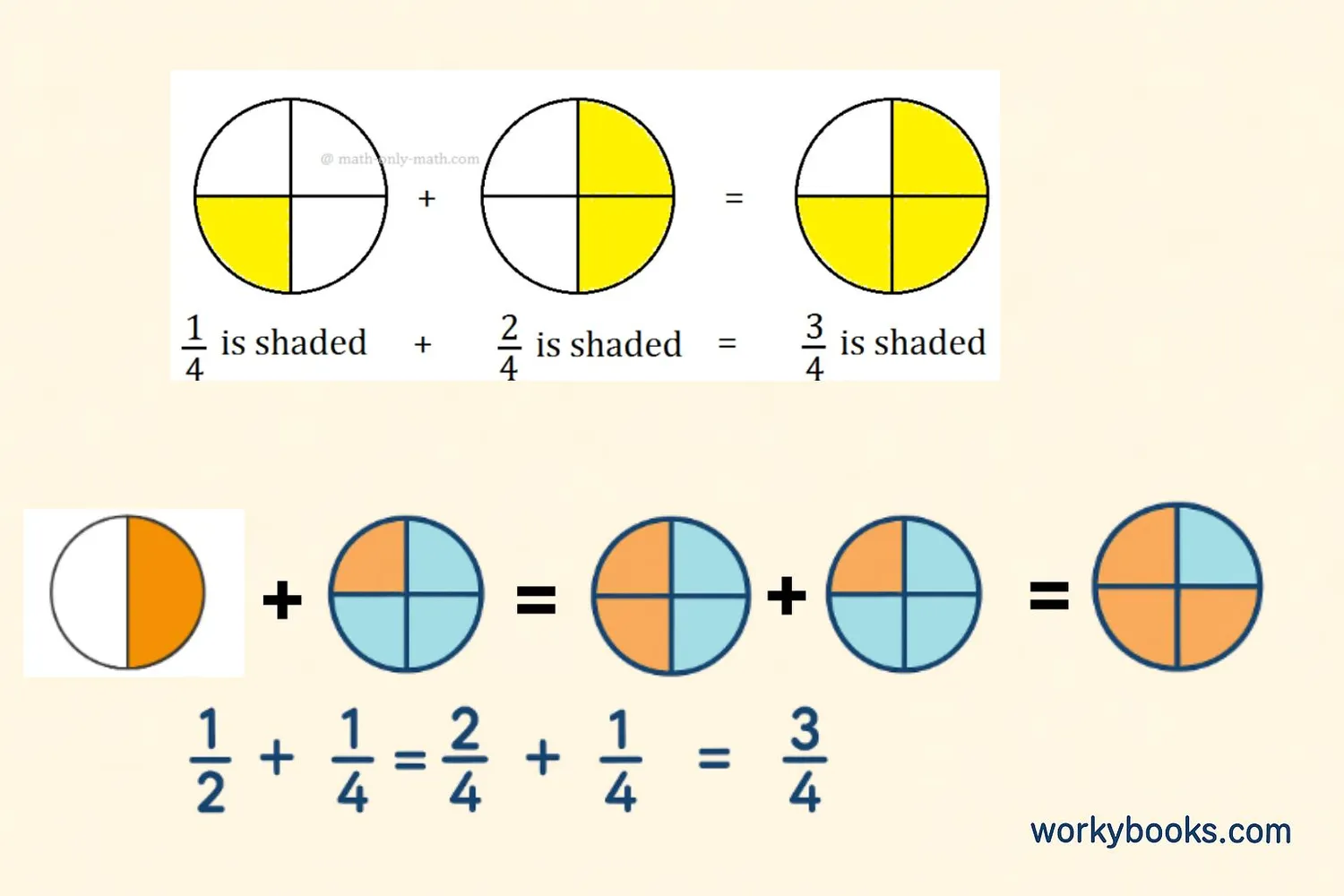
Adding Like Fractions:
When adding like fractions, simply add the numerators and keep the denominator the same.
Example: ²⁄₅ + ¹⁄₅ = ³⁄₅
Subtracting Like Fractions:
When subtracting like fractions, simply subtract the numerators and keep the denominator the same.
Example: ³⁄₄ - ¹⁄₄ = ²⁄₄ = ½
Adding Unlike Fractions:
When adding unlike fractions, first convert them to like fractions with a common denominator, then add the numerators.
Example: ½ + ⅓ = ³⁄₆ + ²⁄₆ = ⁵⁄₆
Subtracting Unlike Fractions:
When subtracting unlike fractions, first convert them to like fractions with a common denominator, then subtract the numerators.
Example: ¾ - ½ = ¾ - ²⁄₄ = ¼
Operation Tip
Always simplify your answers by reducing fractions to their simplest form. For example, ²⁄₄ should be simplified to ½.
Fraction Practice Quiz
Test your understanding of like and unlike fractions with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about like and unlike fractions:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they primarily used unit fractions (fractions with 1 as the numerator). They would write other fractions as sums of unit fractions.
Fraction Line
The horizontal line between the numerator and denominator was introduced by Arabic mathematicians in the 12th century. Before that, fractions were written differently in various cultures.
Fraction Words
The word "fraction" comes from the Latin word "fractus" which means "broken." This makes sense because fractions represent broken or divided parts of a whole.
Fractions in Music
Musical notes are based on fractions! A whole note can be divided into half notes, quarter notes, eighth notes, and so on. This is why understanding fractions helps in reading music.





