Like Denominators - Definition, Examples, Quiz, FAQ, Trivia
Learn to identify and work with fractions that have the same denominator
What Are Like Denominators?
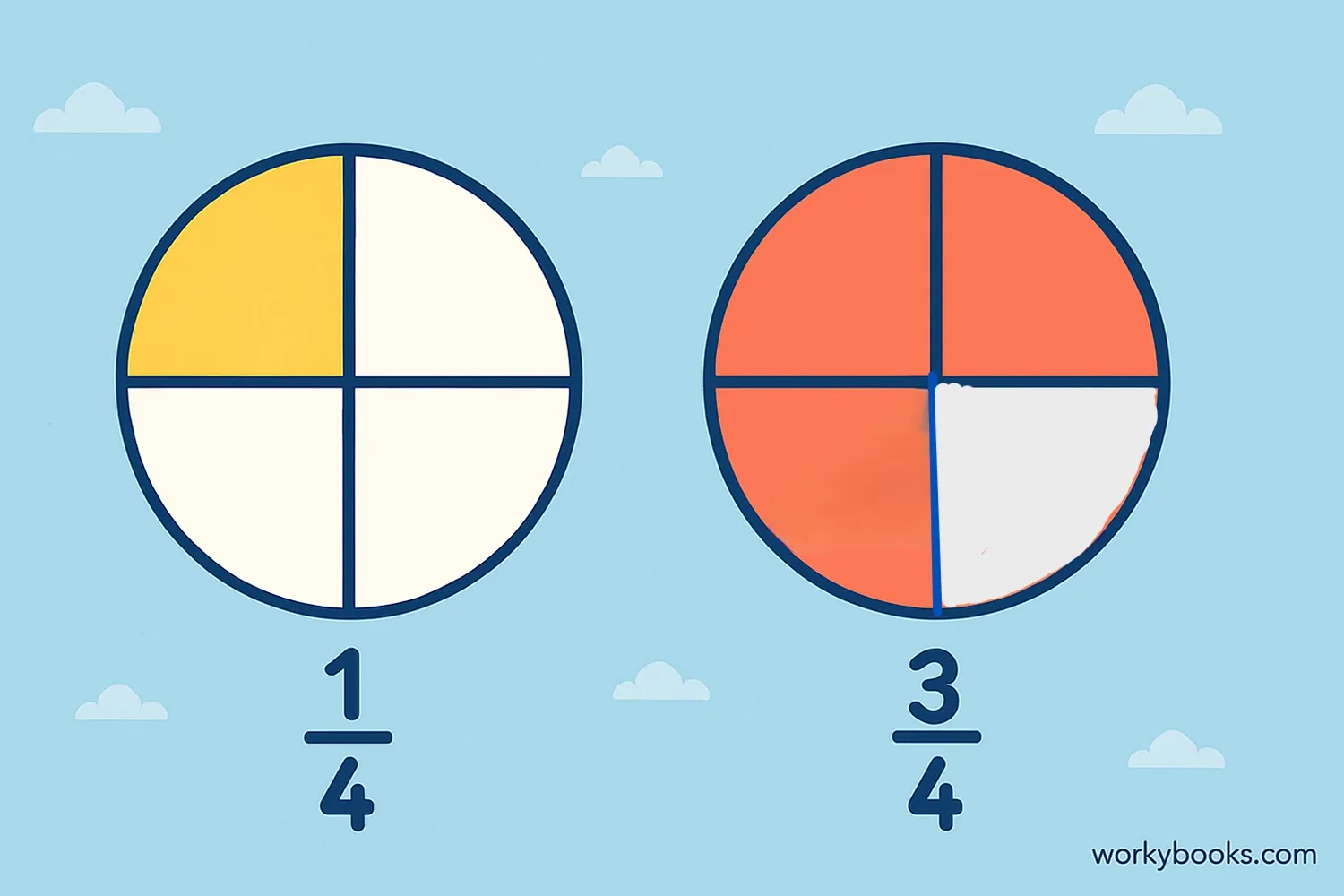
Fractions have two parts: the numerator (top number) and the denominator (bottom number).
Like denominators means the bottom numbers of two or more fractions are the same.
For example, in the fractions
When fractions have like denominators, it means they represent parts of the same-sized whole. This makes them easier to compare and combine.
Key Concept
Like denominators = Same bottom number. Fractions with like denominators represent equal parts of the same whole.
Identifying Like Denominators
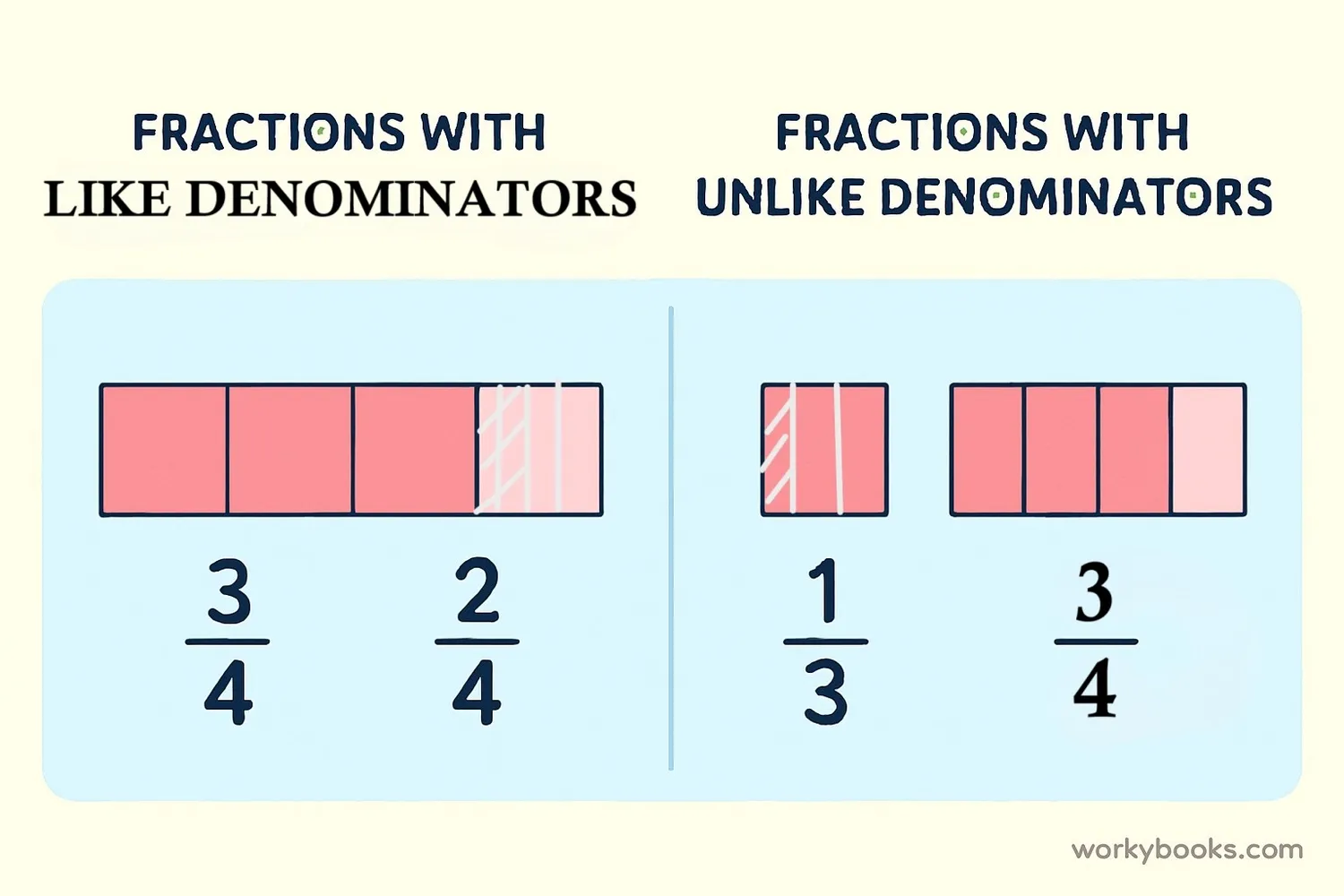
To identify like denominators, look at the bottom number of each fraction. If these numbers are the same, the fractions have like denominators.
Let's look at some examples:
Like Denominators:
Unlike Denominators:
When fractions have unlike denominators, we need to find a common denominator before we can add or subtract them.
Remember
Only look at the bottom number (denominator) to determine if fractions have like denominators. The top numbers (numerators) can be different.
Adding Fractions with Like Denominators
Adding fractions with like denominators is simple! When the denominators are the same, you just add the numerators and keep the same denominator.
Addition Formula
Add the numerators, keep the same denominator
Example: Add
Step 1: Check that denominators are the same → both are 5 ✓
Step 2: Add the numerators → 1 + 2 = 3
Step 3: Keep the same denominator → 5
Step 4: Write the answer →
So
Addition Tip
Imagine adding slices of the same pizza. If the pizza is cut into 8 equal slices, 3 slices + 2 slices = 5 slices, or 3/8 + 2/8 = 5/8.
Subtracting Fractions with Like Denominators
Subtracting fractions with like denominators works the same way as addition. When the denominators are the same, you subtract the numerators and keep the same denominator.
Subtraction Formula
Subtract the numerators, keep the same denominator
Example: Subtract
Step 1: Check that denominators are the same → both are 8 ✓
Step 2: Subtract the numerators → 7 - 3 = 4
Step 3: Keep the same denominator → 8
Step 4: Write the answer →
So
We can simplify
Subtraction Tip
Imagine you have 7/8 of a pizza and you eat 3/8. You have 4/8 or 1/2 left!
Real-World Examples
Let's practice with some real-world examples:
Example 1: Sarah ate
Solution:
Example 2: A recipe calls for
Solution:
Example 3: In a class of 10 students,
Solution:
Example 4: You have
Solution:
Practice Tip
Look for fractions in your daily life - when cooking, measuring, or sharing items. Practice identifying like denominators and adding/subtracting them.
Like Denominators Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about like denominators:
Fraction Trivia
Discover interesting facts about fractions and denominators:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They mainly used unit fractions (fractions with 1 as the numerator) and would write them with a special symbol that looked like a mouth.
Denominator Meaning
The word "denominator" comes from Latin meaning "namer." It names how many equal parts the whole is divided into. The numerator "numbers" or counts how many of those parts we have.
Fractions in Music
Fractions are used in music notation! Time signatures like 3/4 or 4/4 are fractions that tell musicians how many beats are in each measure and what note gets one beat.
Fractions in Measurement
In the United States, rulers are often marked in fractions of an inch (1/2, 1/4, 1/8, 1/16). Carpenters and builders need to be experts at adding and subtracting these fractions!


