Linear Equations - Definition, Examples, Quiz, FAQ, Trivia
Learn about linear equations with easy explanations, examples, and practice activities
What is a Linear Equation?
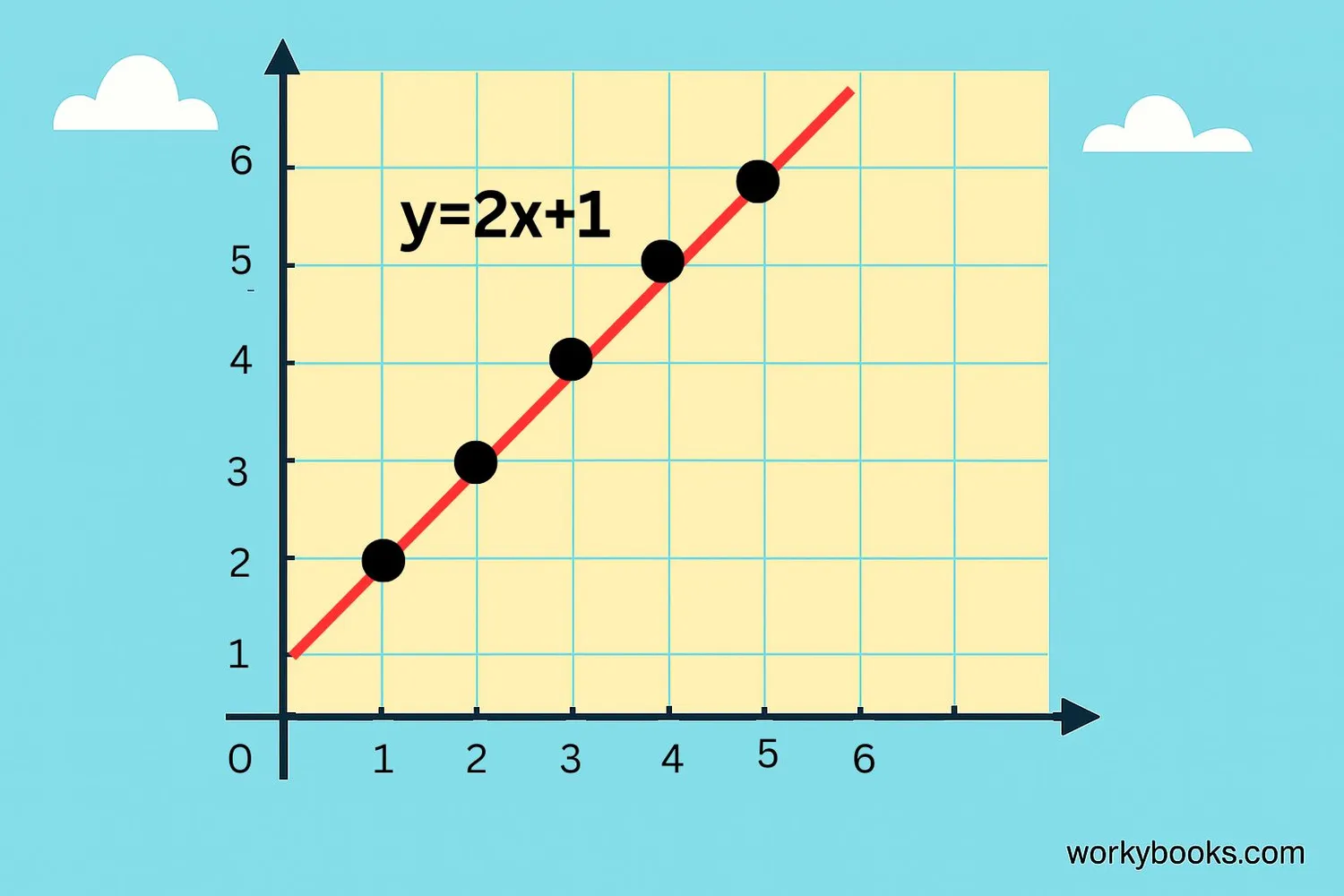
A linear equation is a special type of equation that makes a straight line when you graph it. Think of it as a recipe that tells you how to draw a perfectly straight line on graph paper.
Definition: A linear equation is an equation where the highest power of the variable is 1. This means you won't see exponents like x² or x³ in a linear equation.
Linear equations can have one variable or two variables:
- One variable: 2x + 3 = 7
- Two variables: y = 3x + 2
Key Concept
The word "linear" comes from "line" because these equations always make straight lines when graphed.
Forms of Linear Equations

Linear equations can be written in different forms. Each form is useful for different situations. Let's look at the three main forms:
1. Standard Form
A, B, and C are integers (whole numbers), and A should be positive.
2. Slope-Intercept Form
m is the slope (steepness) and b is the y-intercept (where the line crosses the y-axis).
3. Point-Slope Form
m is the slope, and (x₁, y₁) is a point on the line.
Remember
You can convert between these different forms. The slope-intercept form is often the easiest for graphing!
Solving Linear Equations
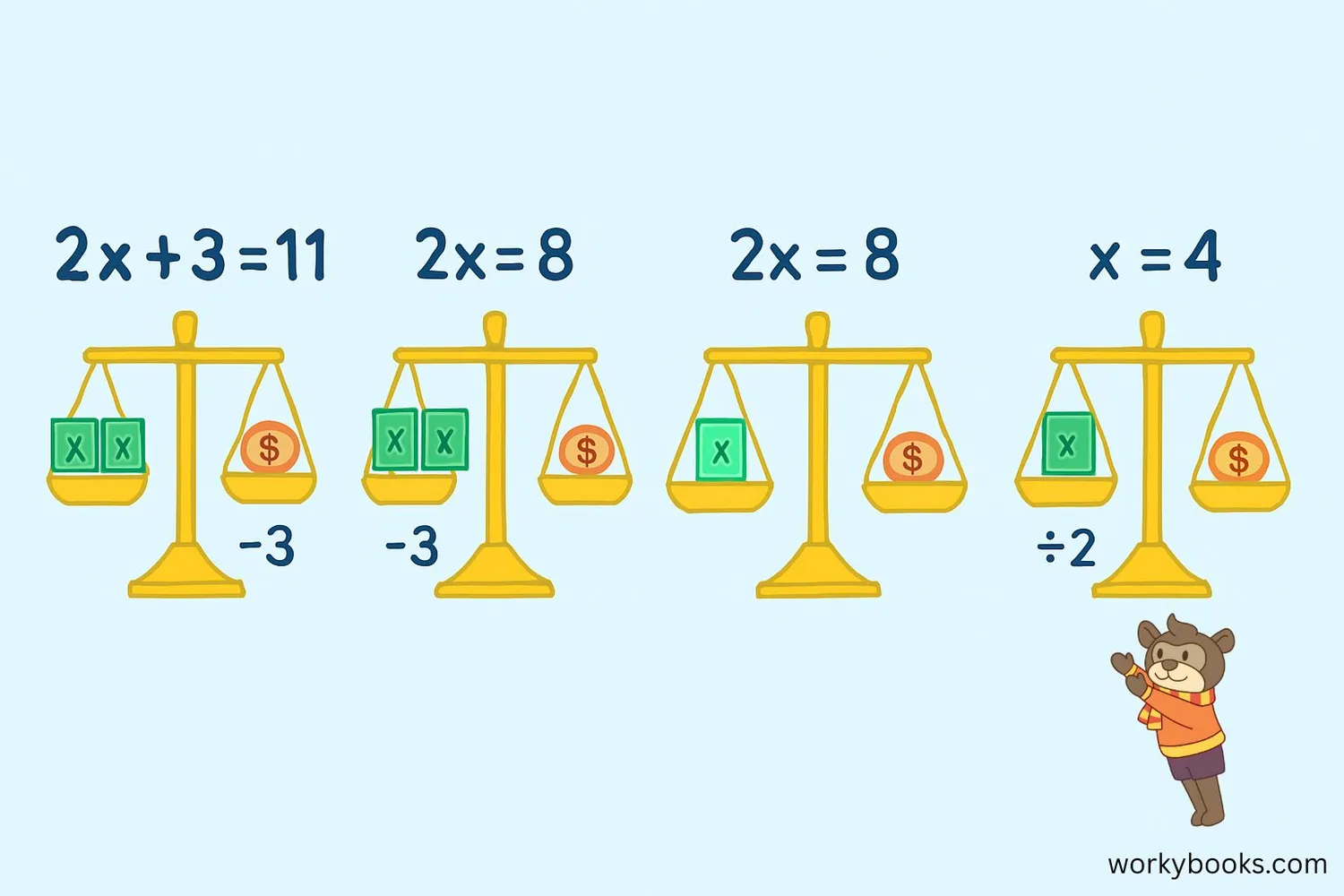
Solving linear equations is like solving a mystery - we want to find the value of the variable that makes the equation true. Here's how to solve a one-variable linear equation:
Example: Solve 3x + 4 = 13
Solving Tip
Whatever you do to one side of the equation, you must do to the other side to keep it balanced!
Graphing Linear Equations
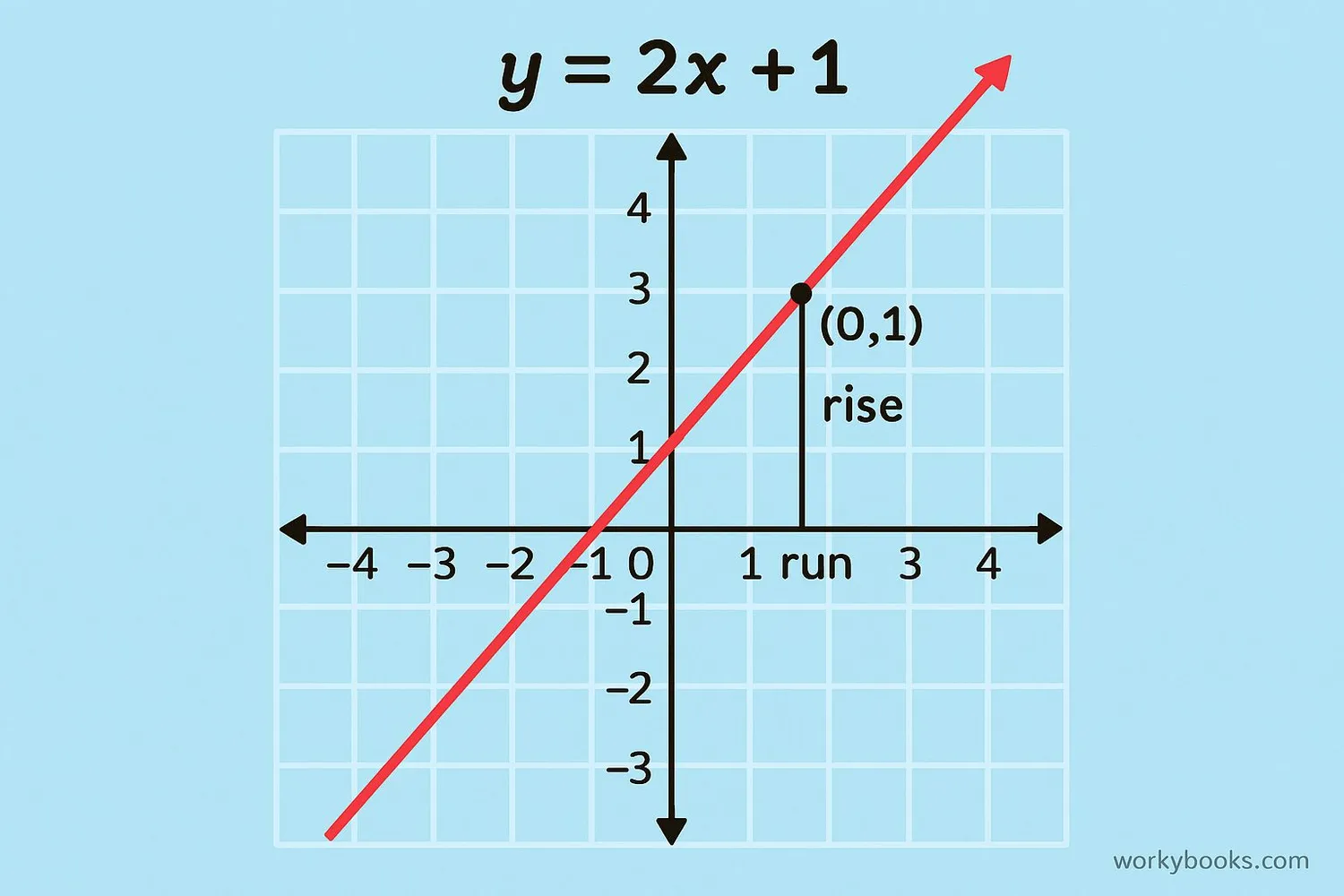
Graphing linear equations helps us see the relationship between variables. Here's how to graph a linear equation in slope-intercept form (y = mx + b):
Graphing y = 2x + 1
Graphing Tip
You only need two points to graph a linear equation, but it's good to find at least three to make sure they line up!
Systems of Linear Equations
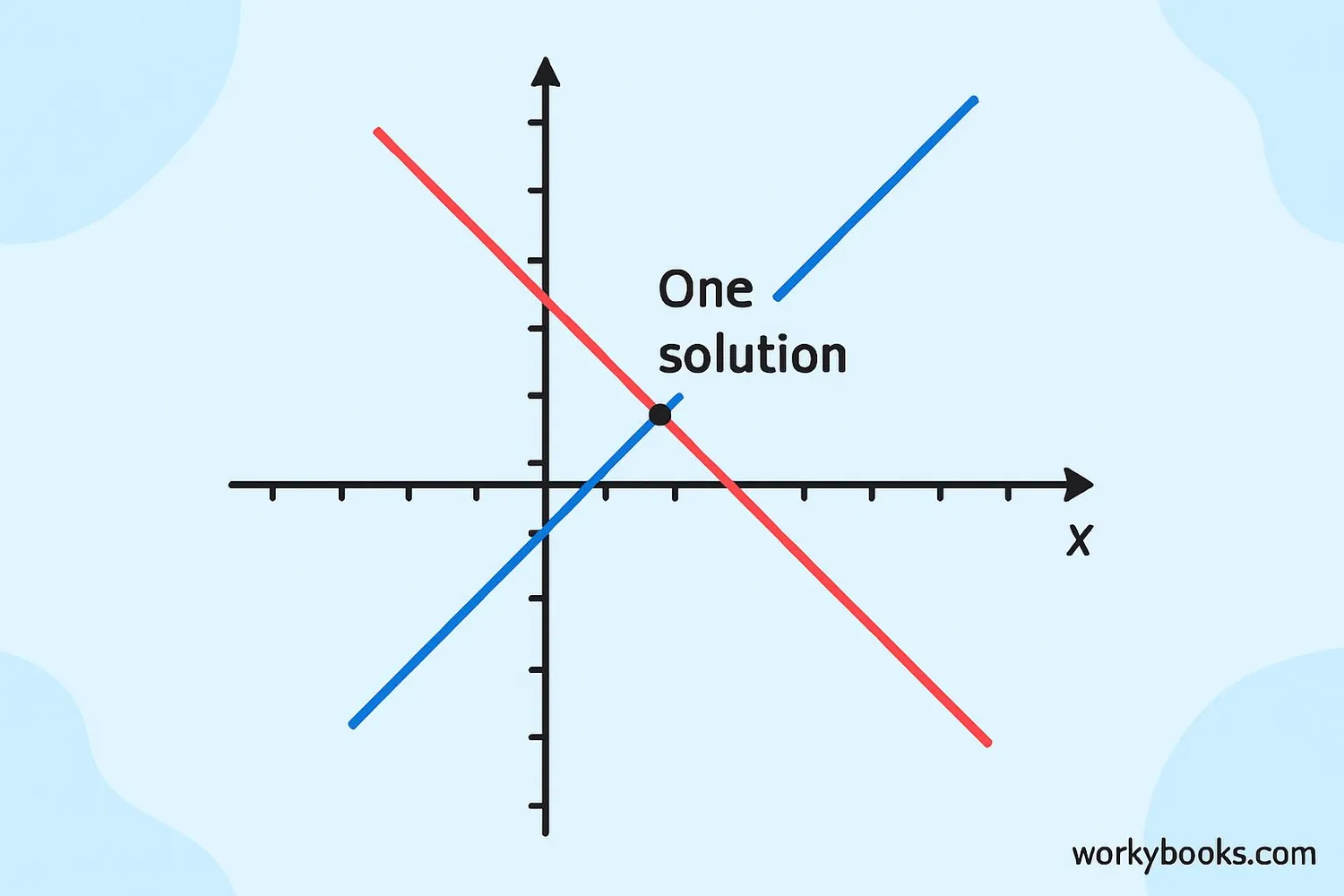
A system of linear equations is when we have two or more linear equations working together. We try to find values for the variables that make all equations true at the same time.
There are three possible outcomes:
- One solution: The lines cross at one point (like an X)
- No solution: The lines are parallel and never cross
- Infinite solutions: The lines are exactly the same
Real-world Application
Systems of equations help solve problems like finding when two people will meet if they're walking toward each other, or comparing cell phone plans.
Linear Equations Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about linear equations:
Math Trivia
Discover interesting facts about equations and mathematics:
Ancient Equations
The earliest recorded linear equations date back to ancient Egypt around 1650 BC! The Rhind Mathematical Papyrus contains problems that we would solve today using linear equations.
Universal Language
Linear equations are used in every country on Earth. Mathematics is truly a universal language, and linear equations are one of its most important "words"!
Space Exploration
NASA engineers use systems of linear equations to calculate spacecraft trajectories. Getting to the Moon required solving thousands of linear equations!
Longest Equation
The longest mathematical equation ever written was a linear system with over 200,000 variables! It was created to model complex weather patterns.





