Linear Pair of Angles - Definition, Examples, Quiz, FAQ, Trivia
Learn about angle relationships formed on a straight line with visual examples and practice activities
What is a Linear Pair of Angles?
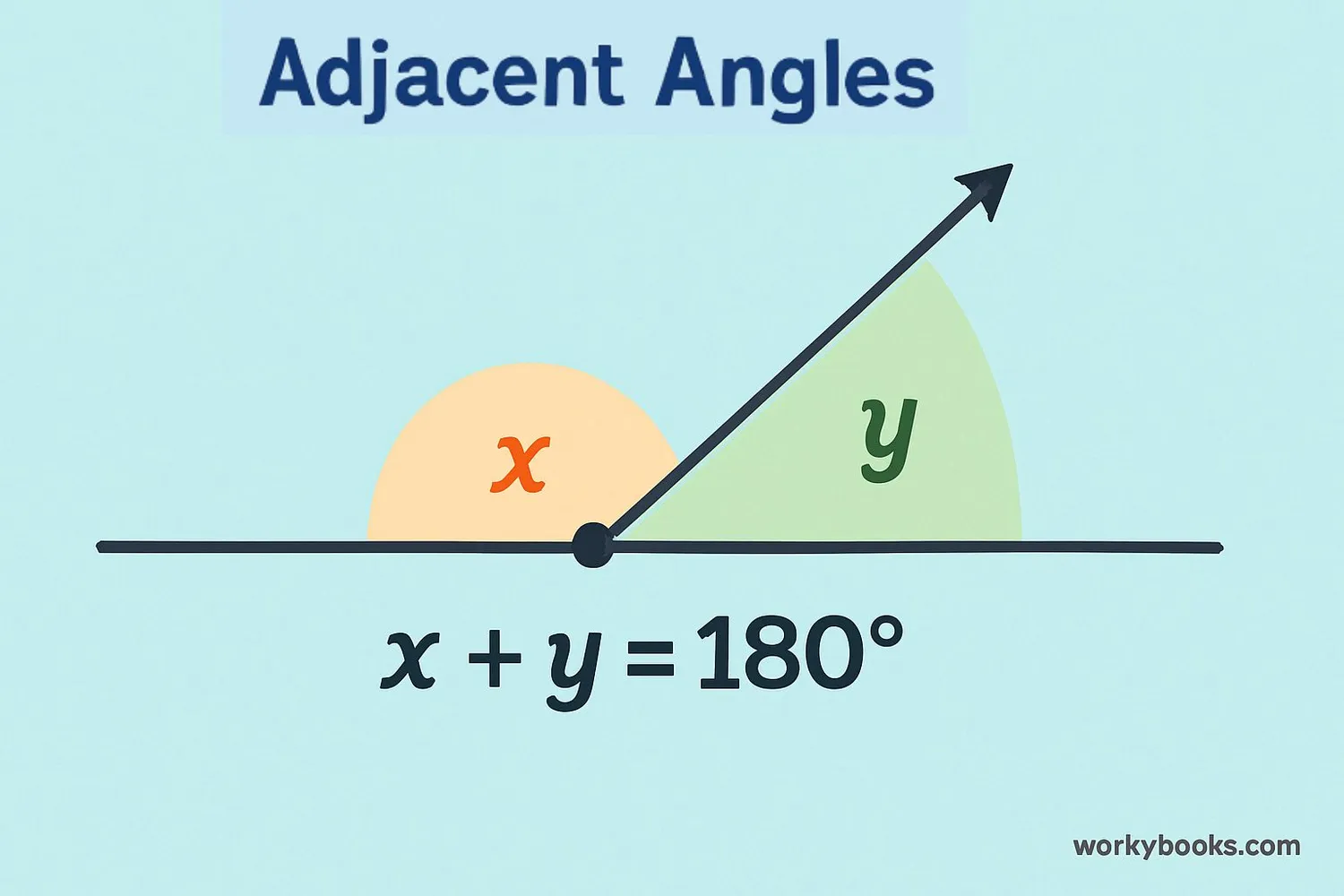
A linear pair of angles is formed when two adjacent angles are created by two intersecting lines. These angles always have two important properties:
1. They are adjacent - meaning they share a common vertex and a common side.
2. Their non-common sides form a straight line - which means they add up to 180 degrees.
When you see a straight line with a ray coming out from a point on that line, you've found a linear pair! The two angles created will always be supplementary, which means they add up to exactly 180 degrees.
Key Concept
A linear pair consists of two adjacent angles whose non-common sides form a straight line. Together, they always measure 180 degrees.
Properties of Linear Pair of Angles
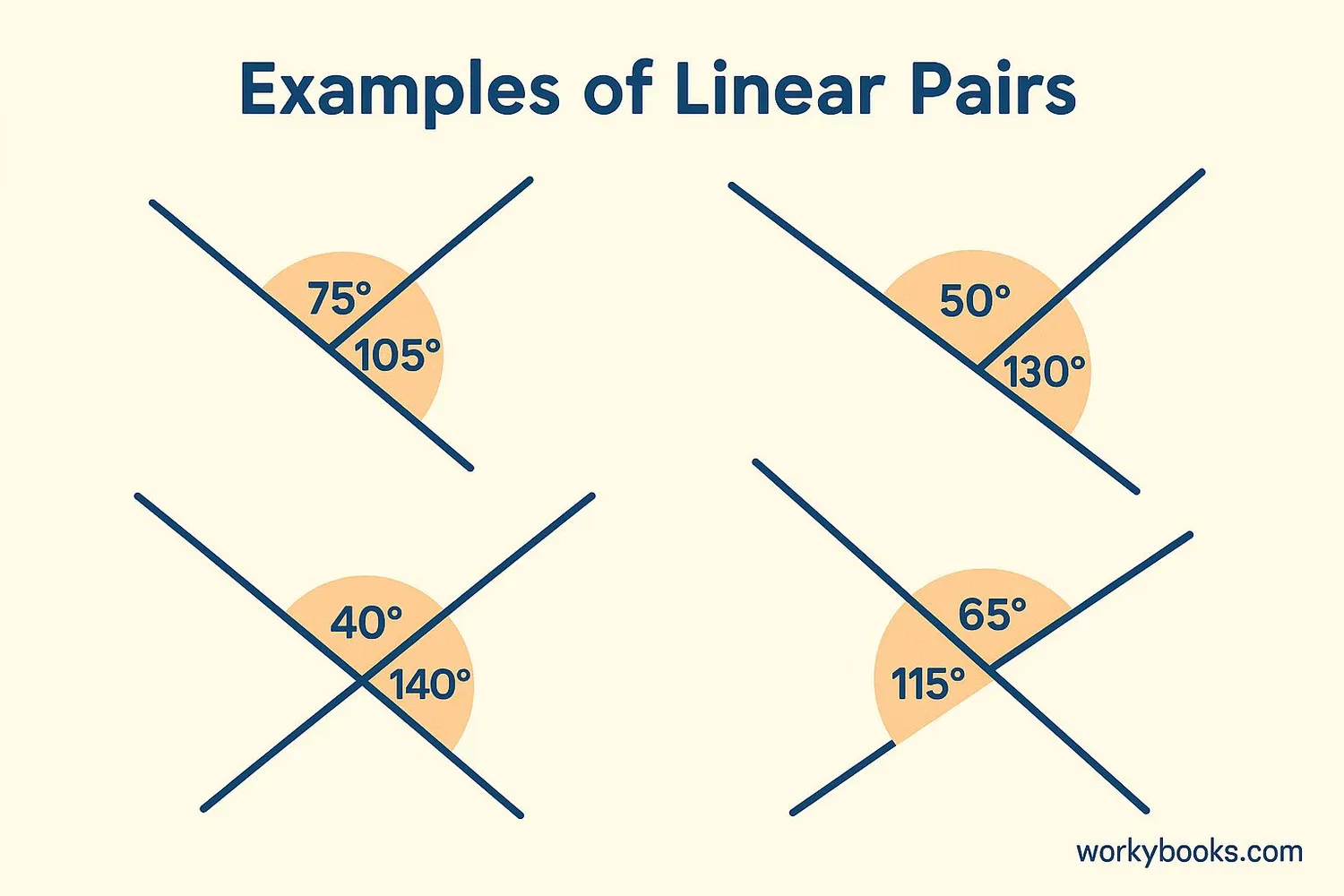
Linear pairs of angles have several important properties that help us solve geometry problems:
- Supplementary Angles: The angles in a linear pair always add up to 180 degrees.
- Adjacent Angles: They share a common vertex and a common side between them.
- Straight Line Formation: Their non-common sides form a straight line.
- Intersecting Lines: Linear pairs are formed when two lines intersect, creating adjacent supplementary angles.
Linear Pair Relationship
If two angles form a linear pair, the sum of their measures is always 180 degrees.
Remember
All linear pairs are supplementary, but not all supplementary angles form a linear pair. To be a linear pair, the angles must also be adjacent.
Linear Pair Axiom
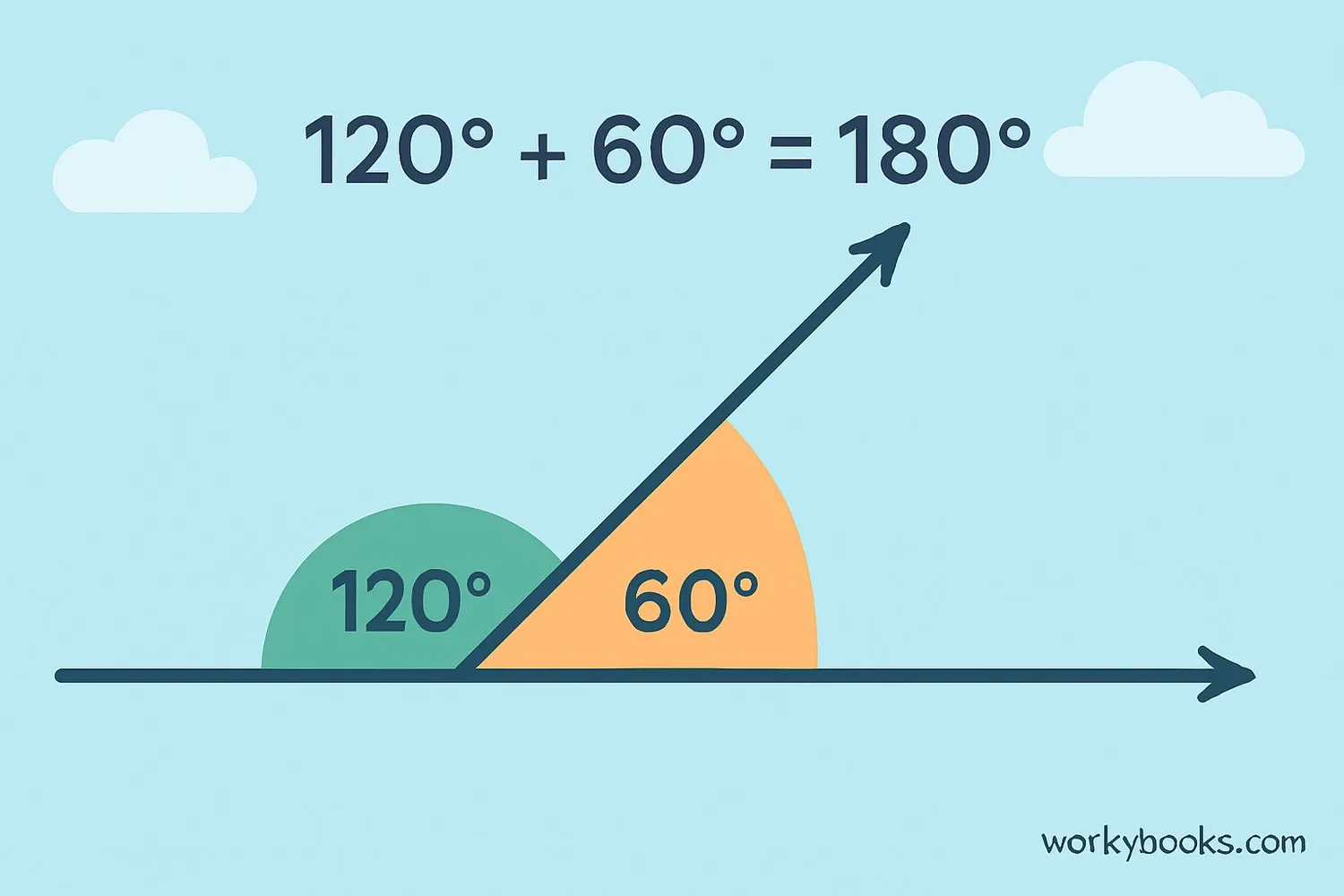
The Linear Pair Axiom is an important rule in geometry that states:
"If a ray stands on a line, then the sum of the two adjacent angles formed is 180 degrees."
This axiom helps us prove many other geometric theorems and solve problems involving angles. It's like a special rule that always works for linear pairs.
We can also state the converse of this axiom: "If the sum of two adjacent angles is 180 degrees, then their non-common arms form a straight line."
This means that if we know two adjacent angles add up to 180 degrees, we can be sure they form a linear pair.
Axiom Tip
The linear pair axiom is a fundamental building block in geometry that helps us prove other important theorems about angles and lines.
Real-World Examples
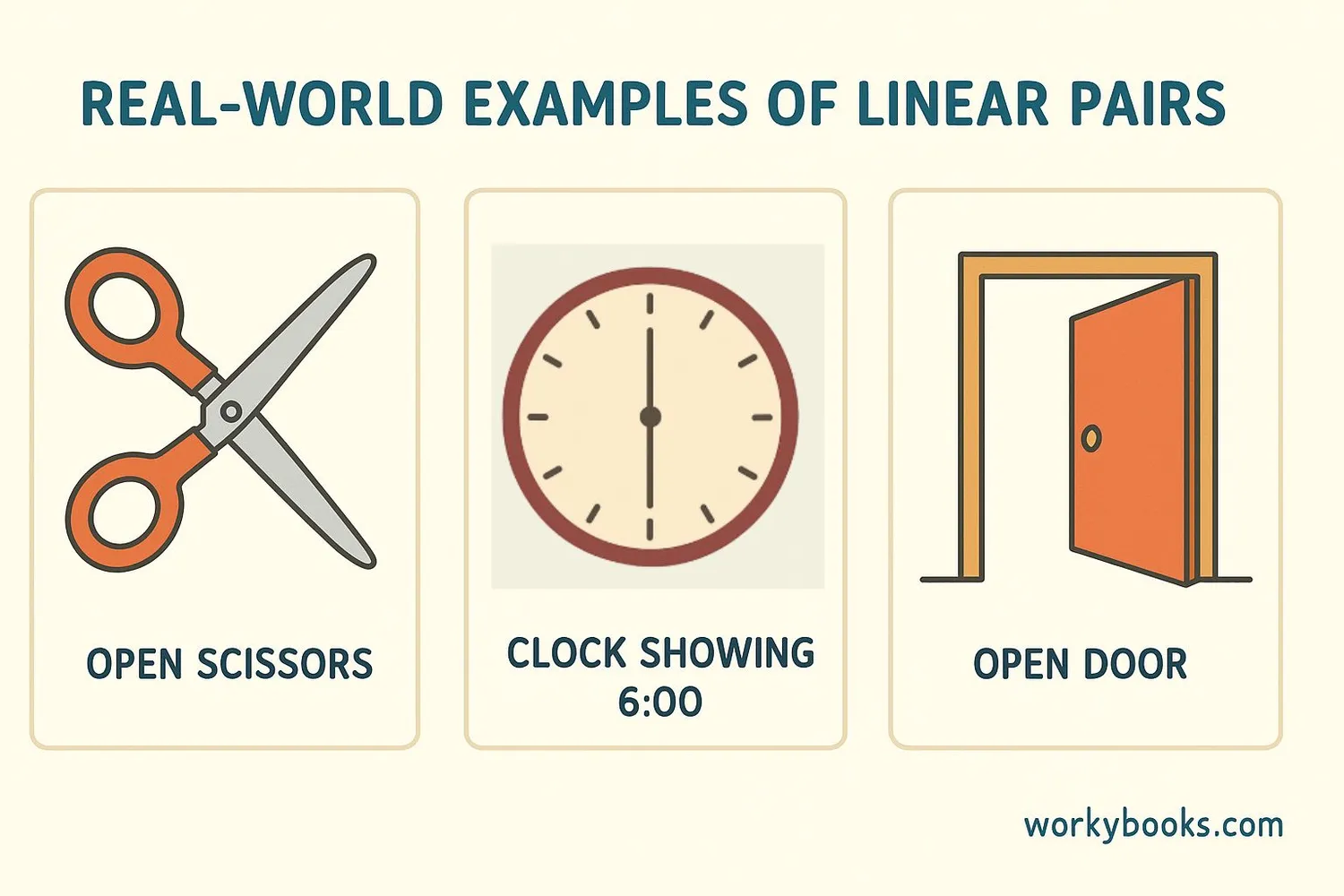
Linear pairs of angles appear in many everyday situations. Let's look at some examples:
Example 1: Scissors - When you open a pair of scissors, the handles and the blades form linear pairs of angles.
Example 2: Clock hands - At 6:00, the hour and minute hands form a straight line, creating a linear pair with the space around them.
Example 3: Door and frame - When a door is open, the angle between the door and the frame and the angle between the door and the wall often form a linear pair.
Example 4: Book opened flat - When a book is opened completely flat, the two pages form a linear pair with the spine of the book.
Let's solve a practice problem:
If one angle in a linear pair measures 115 degrees, what is the measure of the other angle?
Solution: Since linear pairs sum to 180 degrees, the other angle = 180° - 115° = 65°.
Practice Tip
Look for linear pairs in your environment - they're everywhere once you know what to look for!
Practice Quiz
Test your understanding of linear pairs with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about linear pairs of angles:
Geometry Trivia
Discover interesting facts about angles and geometry:
Ancient Geometry
The concept of angles dates back to ancient Babylonian astronomers who divided circles into 360 degrees around 2000 BCE. This number was likely chosen because it has many divisors and is close to the number of days in a year.
Straight Angle
A straight angle measures exactly 180 degrees. The concept of a linear pair relies on this fundamental property of straight angles, as the two angles together form a straight angle.
Angles in Nature
Honeybees use their understanding of angles to communicate food locations to other bees through their "waggle dance," which indicates direction relative to the sun using specific angles.
Architectural Angles
The Leaning Tower of Pisa leans at an angle of about 3.97 degrees. Engineers use principles of angle relationships, including linear pairs, to understand and correct structural issues in buildings.





