Lines of Symmetry in a Rhombus - Definition, Examples, Quiz, FAQ, Trivia
Learn about symmetry in geometry with easy explanations, visual examples, and practice activities
What is a Rhombus?
A rhombus is a special type of quadrilateral (four-sided shape) with some unique properties:
- All four sides are equal in length
- Opposite sides are parallel to each other
- Opposite angles are equal
- Diagonals bisect each other at right angles
Think of a rhombus as a "pushed-over square." If you push on a square from the sides, it becomes a rhombus. A square is actually a special type of rhombus where all angles are 90 degrees.
Key Concept
A rhombus is a quadrilateral with all sides equal in length. This is its most important property.
What are Lines of Symmetry?

A line of symmetry is an imaginary line that divides a shape into two identical halves. When you fold the shape along this line, both halves match exactly.
Think of it like a mirror placed along the line - one side is the reflection of the other. Shapes can have:
No lines of symmetry: Like a scalene triangle
One line of symmetry: Like an isosceles triangle
Multiple lines of symmetry: Like a square or rectangle
Symmetry is all around us in nature, art, and everyday objects. Your face has approximate symmetry, butterflies have symmetry, and many man-made objects are designed with symmetry.
Remember
A line of symmetry divides a shape into two mirror-image halves that match exactly when folded.
Lines of Symmetry in a Rhombus
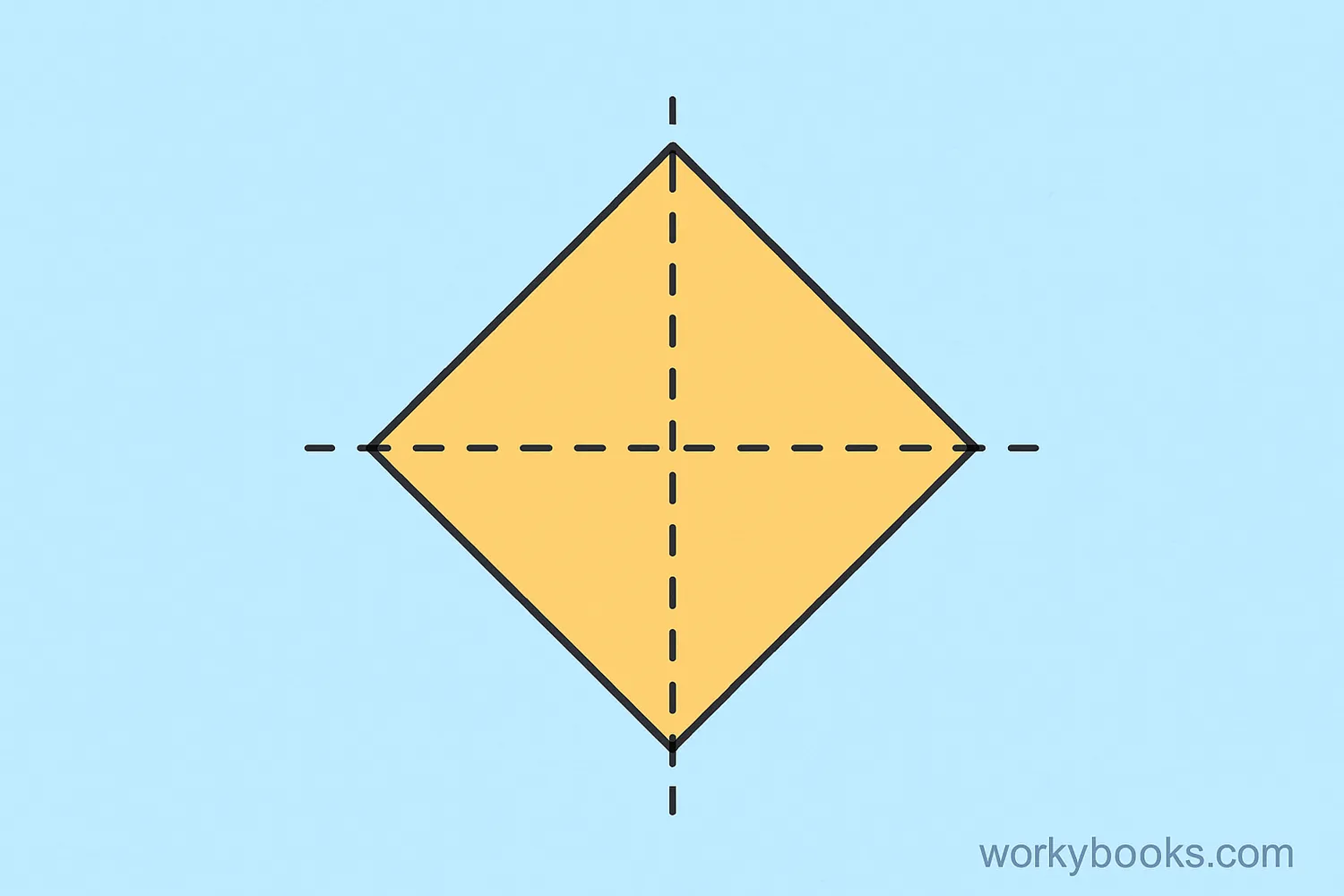
Now let's explore how many lines of symmetry a rhombus has and where they are located:
Key Fact
These lines run along the diagonals of the rhombus
1. The line that goes from one corner to the opposite corner (one diagonal)
2. The line that goes from the other corner to its opposite corner (the other diagonal)
These two lines divide the rhombus into four smaller triangles that are all congruent (exactly the same size and shape).
Important Note
A square is a special type of rhombus that has 4 lines of symmetry (both diagonals and lines through the midpoints of opposite sides).
Examples of Symmetry in Rhombuses
Let's look at some examples to understand symmetry in rhombuses better:
Example 1: A typical rhombus (not a square) with acute angles of 60° and obtuse angles of 120°.
This rhombus has 2 lines of symmetry along its diagonals.
Example 2: A square (which is a special type of rhombus).
A square has 4 lines of symmetry: both diagonals and lines through the midpoints of opposite sides.
Example 3: A rhombus that is very "flat" with very acute angles.
Even when stretched, a rhombus still maintains its 2 lines of symmetry along the diagonals.
Example 4: Real-world objects with rhombus shapes.
Many kites, diamonds, and decorative patterns use rhombus shapes with clear symmetry.
Practice Tip
To find lines of symmetry, imagine folding the shape along a line. If both sides match perfectly, you've found a line of symmetry.
Symmetry Practice Quiz
Test your understanding of symmetry in rhombuses with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about symmetry in rhombuses:
Geometry Trivia
Discover interesting facts about geometry and symmetry:
Ancient Geometry
The word "rhombus" comes from the Greek word "rhombos," which means something that spins. This refers to the shape that spinning tops make when they rotate.
Symmetry in Nature
Many crystals in nature form rhombus shapes due to their molecular structure. Snowflakes, while having hexagonal symmetry, often contain rhombus-shaped patterns within them.
Art and Design
Rhombus patterns have been used in art and architecture for thousands of years. Islamic geometric patterns often feature intricate rhombus designs with multiple lines of symmetry.
Mathematical Property
In a rhombus, the diagonals are always perpendicular bisectors of each other. This means they cross at right angles and cut each other exactly in half, creating the lines of symmetry.





