Long Multiplication - Definition, Examples, Quiz, FAQ, Trivia
Learn to multiply large numbers with step-by-step instructions and practice activities
What is Long Multiplication?
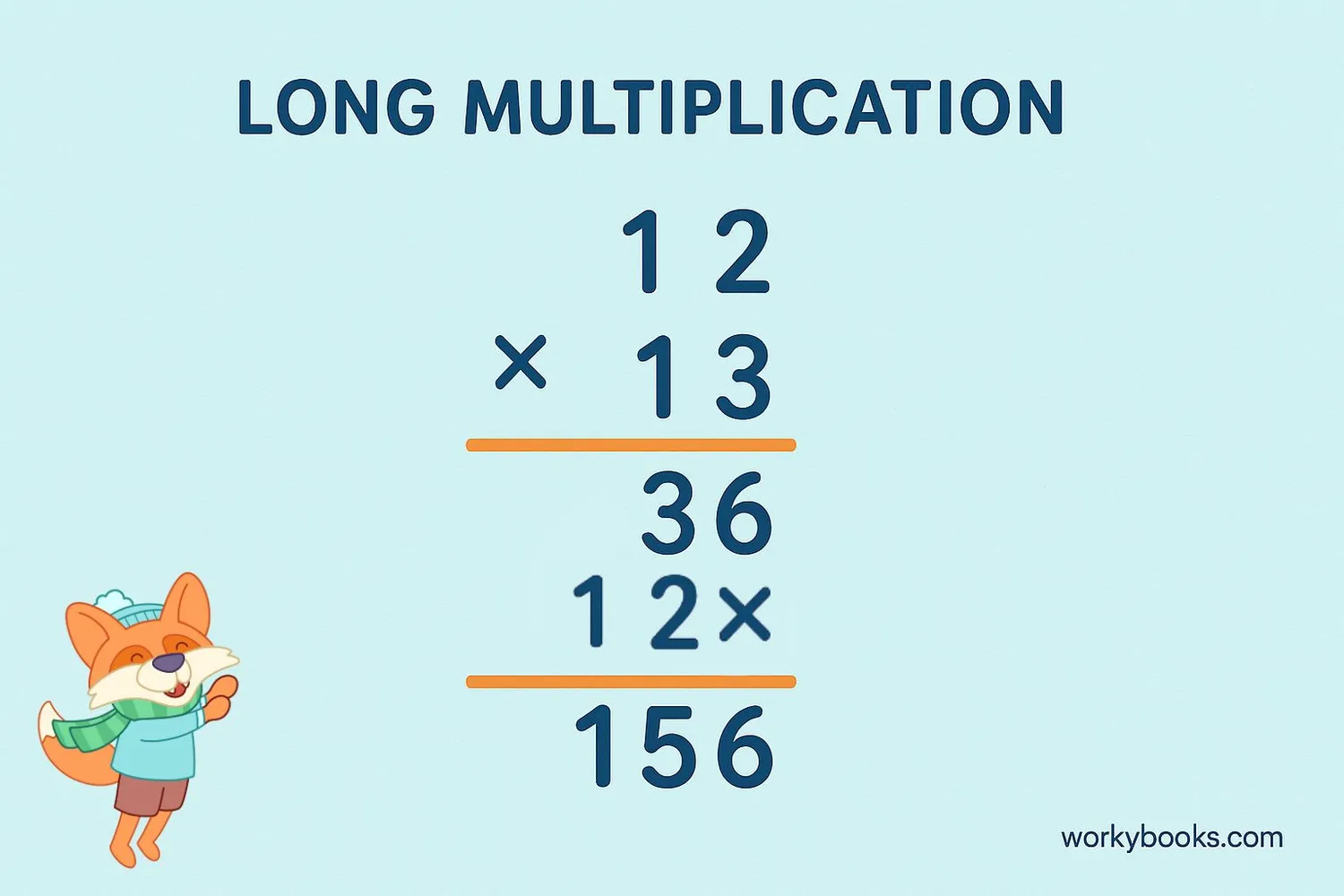
Long multiplication is a method for multiplying larger numbers that are difficult to multiply mentally. It helps us break down complicated multiplication problems into smaller, easier steps that we can solve one at a time.
We use long multiplication when we need to multiply numbers with two or more digits. The method involves writing the numbers one below the other, multiplying each digit separately, and then adding all the results together.
This method is especially helpful when working with numbers that have two or more digits. It ensures we don't miss any place values and helps us keep our work organized.
Key Concept
Long multiplication breaks a large multiplication problem into smaller problems that are easier to solve.
Step-by-Step Long Multiplication

Let's learn how to do long multiplication using these simple steps. We'll use the example 24 × 35 to demonstrate:
1 Write the numbers properly
Write the larger number on top and the smaller number below it. Line up the digits by place value (ones under ones, tens under tens).
× 35
------
2 Multiply by the ones digit
Multiply the top number by the ones digit of the bottom number (5). Write the result below the line.
× 35
------
120 (24 × 5)
3 Multiply by the tens digit
Multiply the top number by the tens digit of the bottom number (3). Write this result one place to the left (add a zero at the end).
× 35
------
120
+72 (24 × 3, then add a zero)
4 Add the results
Add the two products together to get your final answer.
× 35
------
120
+720
------
840
Remember
Always remember to add a zero when you move to the next place value. This is because you're really multiplying by 30, not just 3.
Worked Examples

Let's look at more examples of long multiplication with different numbers:
Example 1: 16 × 25
× 25
------
80 (16 × 5)
+32 (16 × 2, add a zero)
------
400
Example 2: 38 × 47 (with regrouping)
× 47
------
266 (38 × 7)
+152 (38 × 4, add a zero)
------
1786
Notice that 38 × 7 = 266 (we carried the 5 from 56 to the tens place).
Example 3: 123 × 45 (three-digit number)
× 45
------
615 (123 × 5)
+492 (123 × 4, add a zero)
------
5535
Practice Tip
Always double-check your multiplication facts and addition to avoid small mistakes that can lead to wrong answers.
Practice Problems

Try solving these practice problems on your own. Remember to follow all the steps we've learned:
Problem 1: 17 × 23
Try solving this problem step by step.
Problem 2: 34 × 26
Remember to add a zero when you multiply by the tens digit.
Problem 3: 58 × 42
Watch out for regrouping when you multiply.
Problem 4: 126 × 37
This is a three-digit multiplication problem. Take your time!
Answers
1. 391 2. 884 3. 2436 4. 4662
Practice Quiz
Test your long multiplication skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about long multiplication:
Math Trivia
Discover interesting facts about multiplication and numbers:
Ancient Multiplication
The ancient Egyptians used a method called "doubling" to multiply numbers. They would repeatedly double one number and then add up the appropriate doubles to get the product.
Multiplication Patterns
When you multiply any number by 10, you simply add a zero at the end. When you multiply by 100, you add two zeros, and so on. This pattern helps make multiplication easier!
Multiplication Record
The world record for mentally calculating the multiplication of two 13-digit numbers is held by Alexis Lemaire, who solved it in 70.2 seconds!
Zero Property
Any number multiplied by zero equals zero. This is called the zero property of multiplication. It works because multiplication is repeated addition, and adding zero to itself any number of times still equals zero.





