Mean, Median, and Mode - Definition, Examples, Quiz, FAQ, Trivia
Learn about measures of central tendency with examples, practice problems, and quizzes
What Are Mean, Median, and Mode?

Mean, median, and mode are three different ways to describe the center of a set of numbers. They're called measures of central tendency because they show where the middle or center of the data is.
Mean is the average of all the numbers. You find it by adding all numbers together and then dividing by how many numbers there are.
Median is the middle number when all numbers are listed in order. If there are two middle numbers, you take the average of those two.
Mode is the number that appears most often in the set. Some sets have no mode, and some have more than one mode.
Key Concept
Mean = Average, Median = Middle, Mode = Most frequent. These three measures help us understand data in different ways.
Finding the Mean
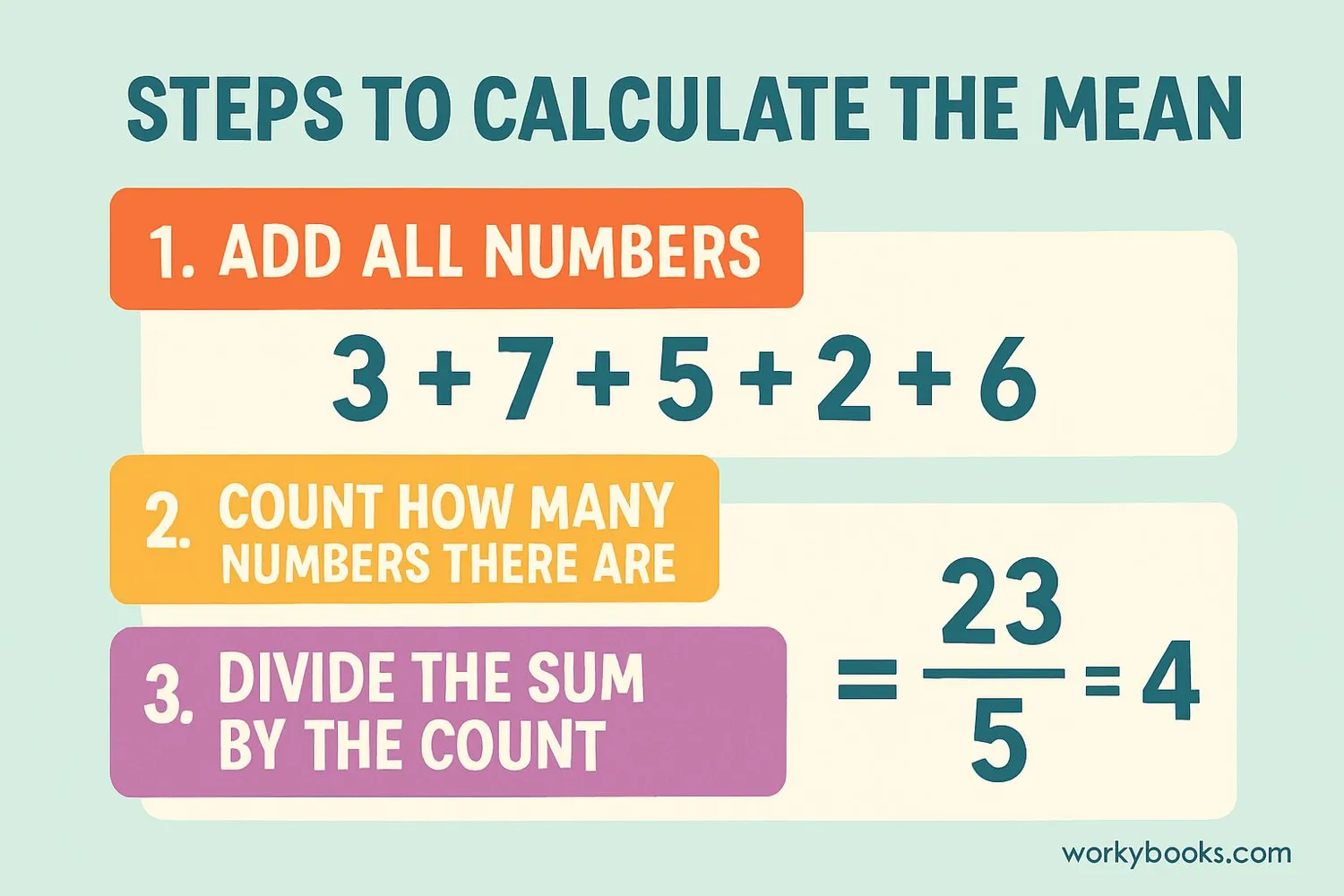
The mean is what we usually call the "average." It's the most common measure of central tendency. Here's how to find it:
Mean Formula
Add all the numbers together, then divide by how many numbers there are.
Example: Find the mean of 5, 7, 3, 8, 2
Step 1: Add all numbers → 5 + 7 + 3 + 8 + 2 = 25
Step 2: Count the numbers → There are 5 numbers
Step 3: Divide the sum by the count → 25 ÷ 5 = 5
So the mean is 5.
Remember
The mean can be affected by very large or very small numbers in your data set. One extreme number can pull the mean up or down.
Finding the Median
The median is the middle number in an ordered list. It's useful when you have extreme numbers that might make the mean misleading.
Here's how to find the median:
1. Put all numbers in order from smallest to largest
2. Find the middle number:
- If there's an odd number of values, the median is the middle one
- If there's an even number of values, the median is the average of the two middle numbers
Example 1 (odd count): Find the median of 12, 3, 7, 5, 10
Step 1: Order the numbers → 3, 5, 7, 10, 12
Step 2: Find the middle → 7 is the median
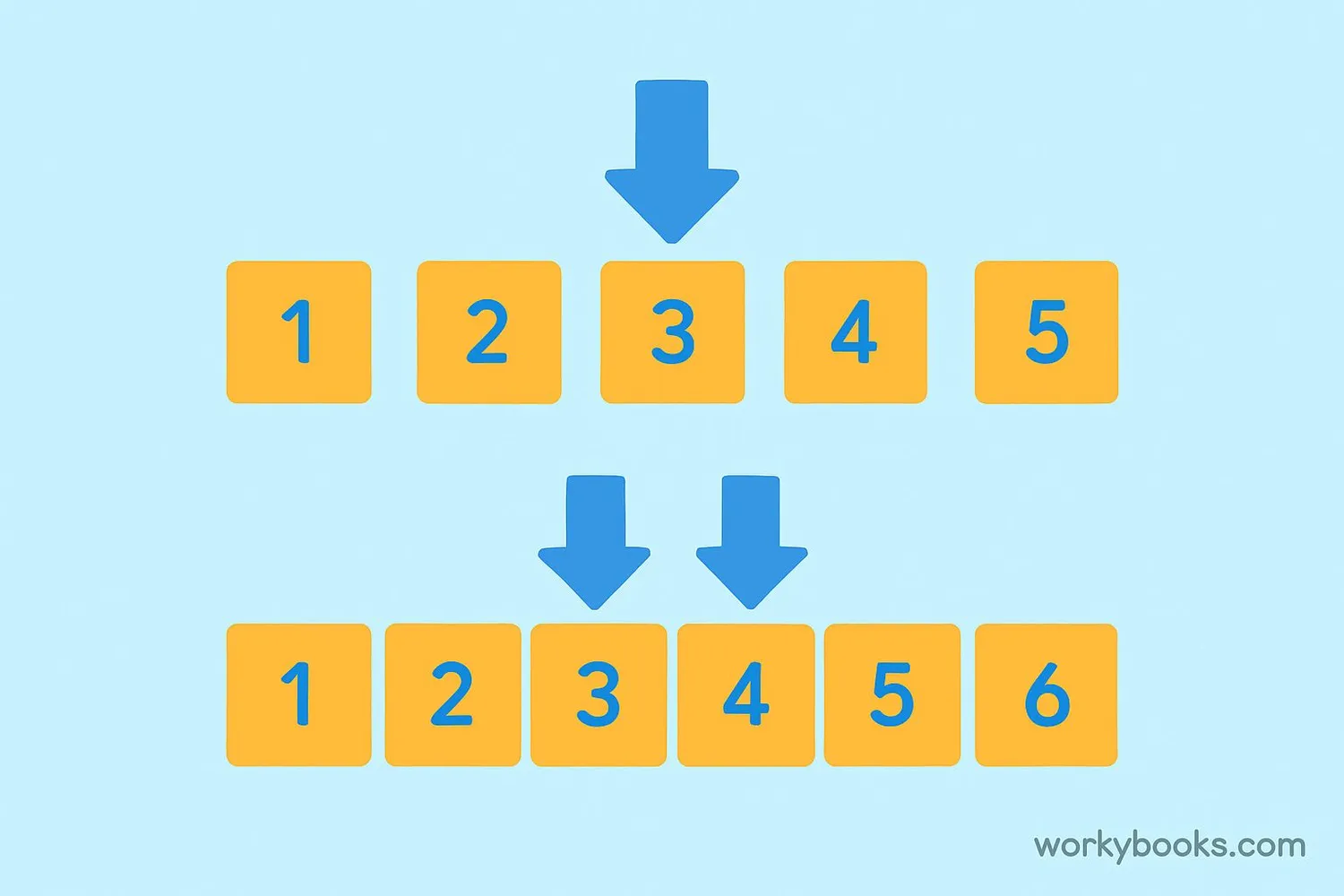
Example 2 (even count): Find the median of 4, 8, 2, 6
Step 1: Order the numbers → 2, 4, 6, 8
Step 2: Find the middle two → 4 and 6
Step 3: Average them → (4 + 6) ÷ 2 = 5
The median is 5
Median Tip
The median isn't affected by extremely high or low numbers, which makes it useful for data with outliers.
Finding the Mode
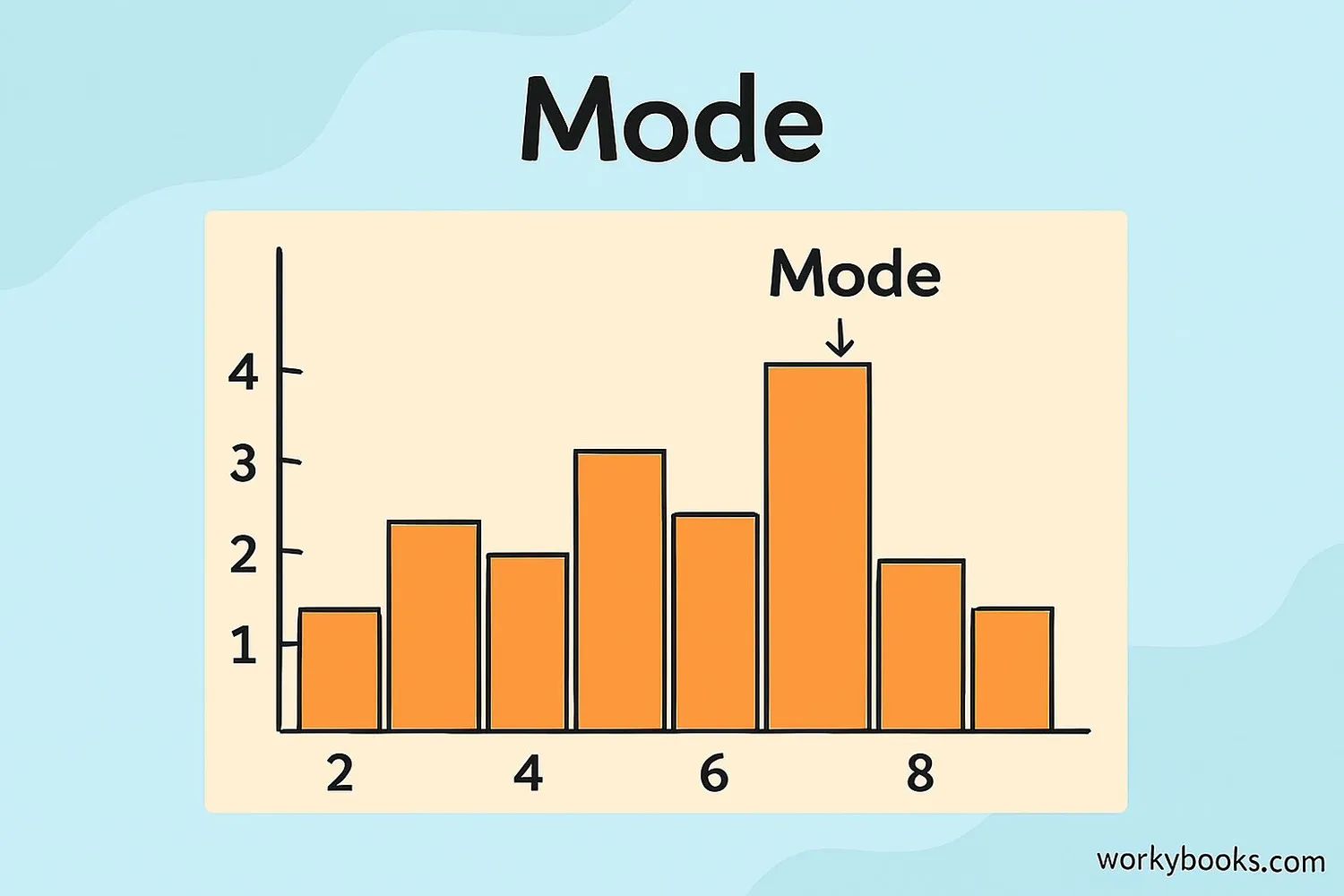
The mode is the number that appears most often in a data set. Some sets have no mode, some have one mode, and some have multiple modes.
Here's how to find the mode:
1. Count how many times each number appears
2. The number(s) that appear most often are the mode(s)
Example 1: Find the mode of 2, 4, 6, 4, 8, 4, 9
- 2 appears 1 time
- 4 appears 3 times
- 6 appears 1 time
- 8 appears 1 time
- 9 appears 1 time
The mode is 4 because it appears most often
Example 2: Find the mode of 1, 2, 3, 4
All numbers appear once → There is no mode
Example 3: Find the mode of 2, 2, 3, 3, 4
Both 2 and 3 appear twice → The modes are 2 and 3
Mode Tip
The mode is especially useful for categorical data (like favorite colors or types of pets) where we can't calculate a mean or median.
Real-World Examples

Let's see how mean, median, and mode are used in everyday situations:
Example 1: Test Scores (Mean)
A teacher wants to find the average test score for her class:
Scores: 85, 90, 78, 92, 88, 76, 95, 85
Mean: (85+90+78+92+88+76+95+85) ÷ 8 = 86.125
The average score is about 86
Example 2: House Prices (Median)
A real estate agent lists prices of homes on a street:
Prices: $200,000, $250,000, $275,000, $300,000, $2,500,000
The mean would be skewed by the expensive house, so the median is better:
Ordered prices: $200K, $250K, $275K, $300K, $2.5M
Median: $275,000
Example 3: Shoe Sizes (Mode)
A shoe store owner wants to know which size to stock most:
Sizes sold last week: 6, 6, 7, 7, 7, 7, 8, 8, 9, 10
Mode: 7 (appears most frequently)
The store should have more size 7 shoes in stock
Practice finding mean, median, and mode with numbers around you - ages of family members, temperatures for the week, or scores from games!
Practice Tip
Try calculating all three measures for the same data set to see how they compare. This helps you understand when each measure is most useful.
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about mean, median, and mode:
Math Trivia
Discover interesting facts about statistics and measurement:
Ancient Averages
The concept of average dates back to ancient Greece. Astronomers used averages to account for measurement errors when tracking stars and planets.
Average Human
Statisticians calculate "average" humans for various measurements. For example, the average adult human body temperature is 98.6°F (37°C), though recent studies suggest it might be slightly lower.
Space Statistics
NASA uses median values when analyzing space data because extreme values (like very high temperatures or radiation levels) could skew averages and give misleading information.
Most Common Birthday
Statistical analysis shows September is the most common birth month in the United States. The mode (most frequent) birthday is September 9th, with September 19th a close second.


