Mean Value Theorem - Definition, Examples, Quiz, FAQ, Trivia
Discover how math helps us understand motion and change with this important concept
What is the Mean Value Theorem?
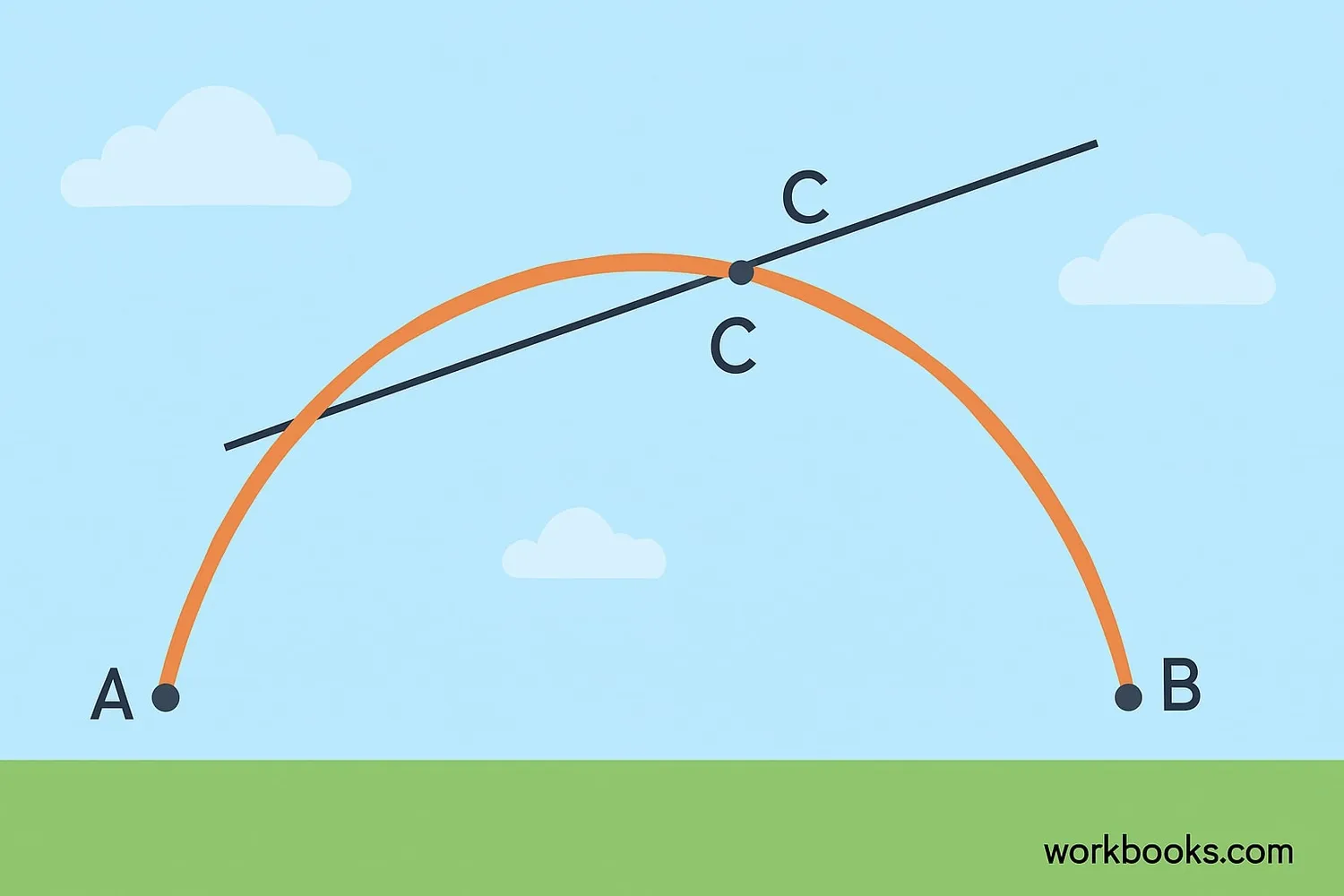
The Mean Value Theorem (MVT) is a special idea in math that helps us understand how things change. Imagine you're taking a car trip from your home to grandma's house. The Mean Value Theorem tells us that at some point during your trip, your speed must have been exactly equal to your average speed for the whole journey!
In math terms, if you have a smooth, continuous curve between two points, there's always at least one point on that curve where the slope (steepness) of the tangent line is equal to the slope of the straight line connecting the two endpoints.
MVT Formula
This formula shows that at some point c between a and b, the slope equals the average slope
Key Concept
The Mean Value Theorem connects the average change over an interval to the instantaneous change at a specific point.
Rolle's Theorem
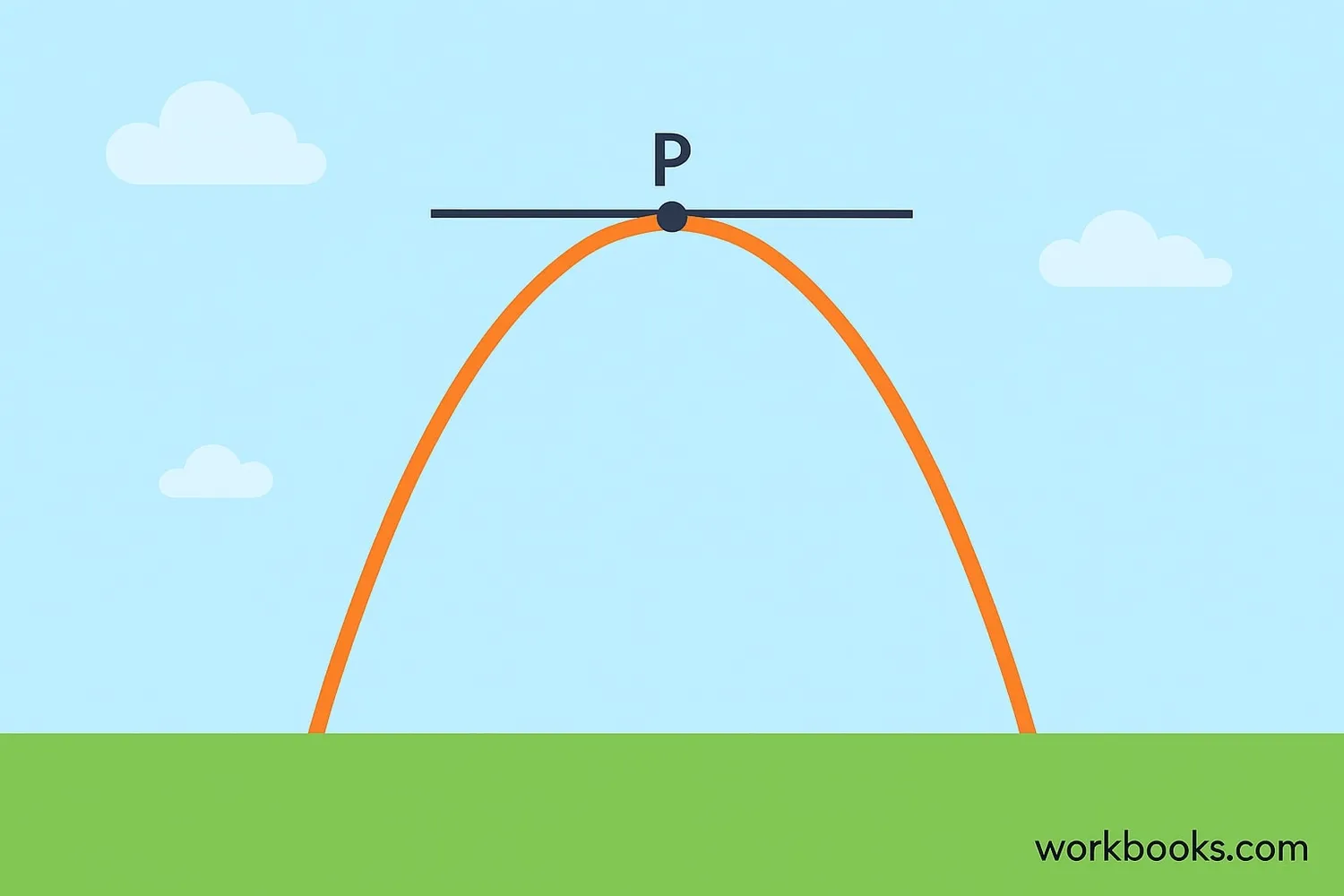
Rolle's Theorem is a special case of the Mean Value Theorem. It says that if you have a smooth curve that starts and ends at the same height, then somewhere between those points, there must be at least one point where the curve is perfectly flat (horizontal).
Think about throwing a ball straight up in the air. It goes up, stops for a moment at the highest point, then comes down. That moment when it stops at the top? That's like the point in Rolle's Theorem where the slope is zero!
Rolle's Theorem Statement
If a function f is continuous on [a, b], differentiable on (a, b), and f(a) = f(b), then there exists at least one c in (a, b) such that f'(c) = 0.
Real-world Application
Rolle's Theorem explains why there's always a moment when a roller coaster at the top of a hill has zero speed before it comes down.
Lagrange's Mean Value Theorem
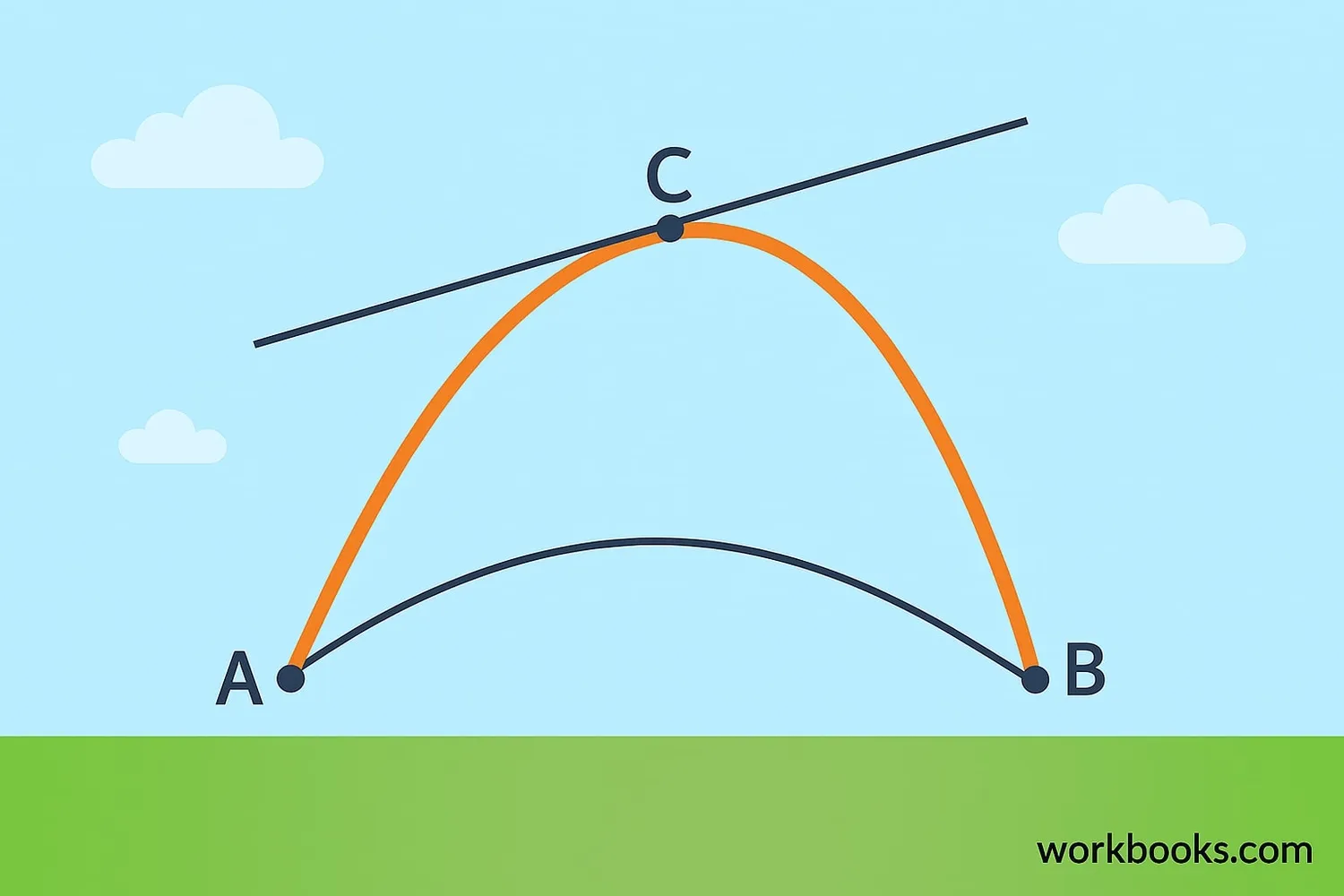
Lagrange's Mean Value Theorem is the general version of the theorem we talked about earlier. It's named after the mathematician Joseph-Louis Lagrange. This theorem tells us that for any smooth curve between two points, there's always at least one point where the tangent line is parallel to the straight line connecting those two points.
Imagine hiking up a hill. If your starting point is at 100 meters and your ending point is at 400 meters, and you hiked for 2 hours, your average climbing speed would be 150 meters per hour. Lagrange's theorem says that at some moment during your hike, you were climbing at exactly 150 meters per hour.
Remember
Rolle's Theorem is just a special case of Lagrange's Mean Value Theorem where the starting and ending points are at the same height.
Mean Value Theorem for Integrals
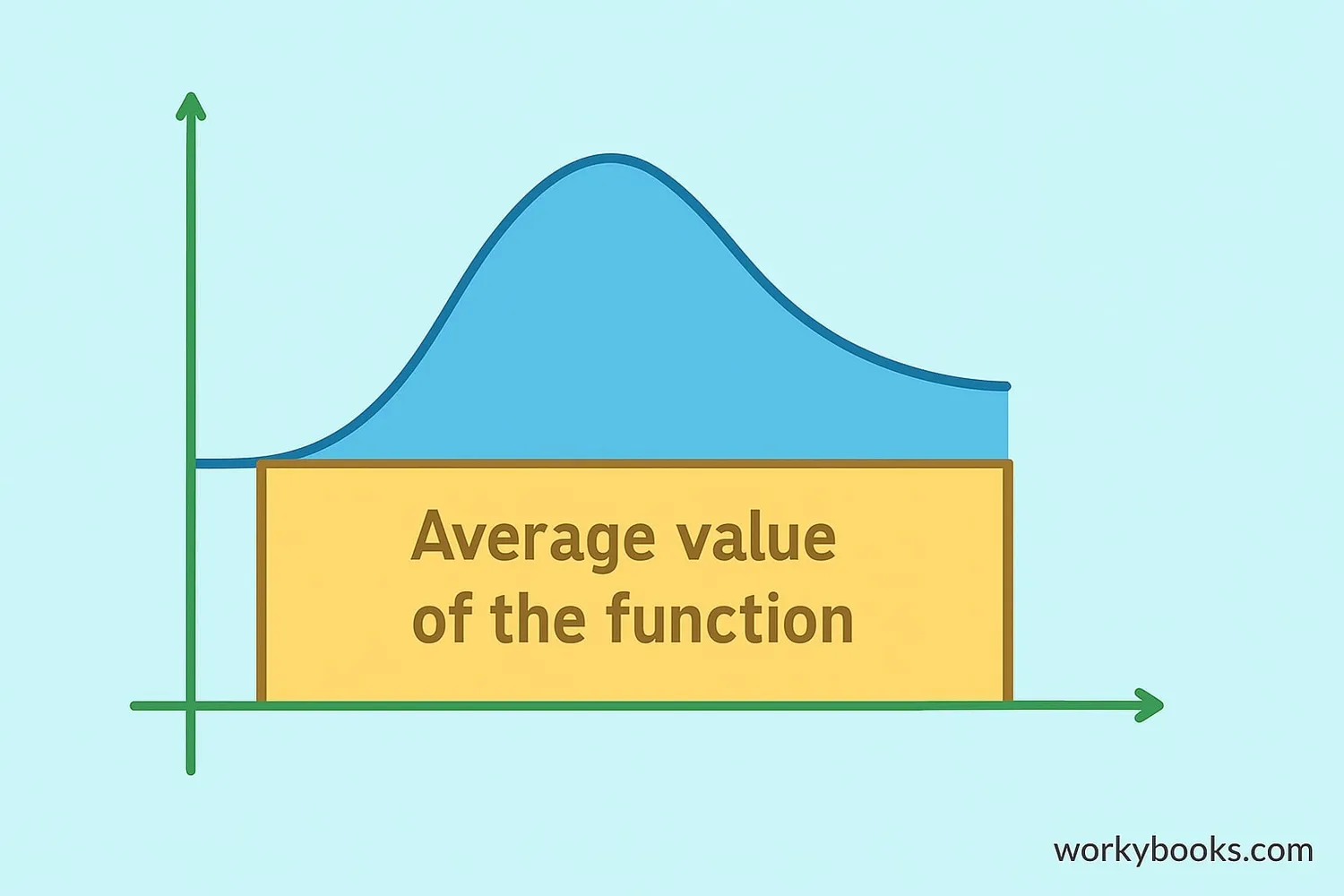
There's also a version of the Mean Value Theorem for integrals. This one tells us about the average value of a function over an interval. It says that for a continuous function, there's always at least one point where the function value equals the average value over the entire interval.
Think about the temperature during a day. If the average temperature was 20°C, the Mean Value Theorem for integrals tells us that at some moment during the day, the temperature was exactly 20°C (assuming the temperature changed continuously).
Average Value Formula
This shows the function value at c equals the average value from a to b
Real-world Application
This theorem helps engineers calculate average forces, temperatures, or speeds in their designs.
Real-World Examples

Example 1: Car Trip
If you drive 150 miles in 3 hours, your average speed is 50 mph. The MVT guarantees that at some point during your trip, your speedometer showed exactly 50 mph.
Example 2: Temperature Change
If the temperature at 8 AM is 15°C and at 2 PM is 25°C, the average temperature over this period is 20°C. The MVT says that at some time between 8 AM and 2 PM, the temperature was exactly 20°C.
Example 3: Stock Market
If a stock price starts at $100 at 9 AM and ends at $110 at 4 PM, the average growth rate is $10/7 ≈ $1.43 per hour. MVT says at some moment during the day, the stock was growing at exactly $1.43 per hour.
Example 4: Battery Drain
If your phone battery goes from 100% to 20% over 10 hours, the average drain rate is 8% per hour. MVT guarantees that at some moment, the battery was draining at exactly 8% per hour.
Why It Matters
The Mean Value Theorem helps mathematicians prove other important theorems and helps engineers design safe bridges, roads, and vehicles.
Practice Quiz
Test your understanding with these multiple-choice questions. Choose the best answer for each question.
Frequently Asked Questions
Here are answers to common questions about the Mean Value Theorem:
Math Trivia
Discover interesting facts about the Mean Value Theorem and mathematics:
Historical Origins
The Mean Value Theorem was first stated by Augustin-Louis Cauchy in 1823. However, the idea was used earlier by mathematicians like Joseph-Louis Lagrange and even by Indian mathematician Parameshvara in the 14th century.
Motion and Physics
In physics, the Mean Value Theorem explains why your average speed during a trip must match your instantaneous speed at some point. This principle is crucial for understanding motion in calculus-based physics.
Space Exploration
NASA engineers use the Mean Value Theorem when calculating rocket trajectories. They need to ensure that at some point during the flight, the rocket's speed matches the average speed needed to reach its destination.
Mathematical Precision
The Mean Value Theorem is so precise that it even applies to the tiny movements of atoms and molecules! At the quantum level, physicists use similar principles to understand particle behavior.


