Median - Definition, Examples, Quiz, FAQ, Trivia
Learn to find the middle value in data with simple explanations and practice activities
What is the Median?

The median is the middle value in a set of numbers when they are arranged in order from smallest to largest. It's one of the three main measures of central tendency, along with mean and mode.
Why is median important? It helps us understand what's typical in a group of numbers. Unlike the mean (average), the median isn't affected by extremely high or low values. This makes it especially useful when we have data with outliers.
Imagine lining up your classmates by height. The person in the middle represents the median height of the class. This value gives us a good idea of the typical height without being skewed by the tallest or shortest person.
Key Concept
The median is the middle number in an ordered list. For an even number of values, it's the average of the two middle numbers.
How to Find the Median
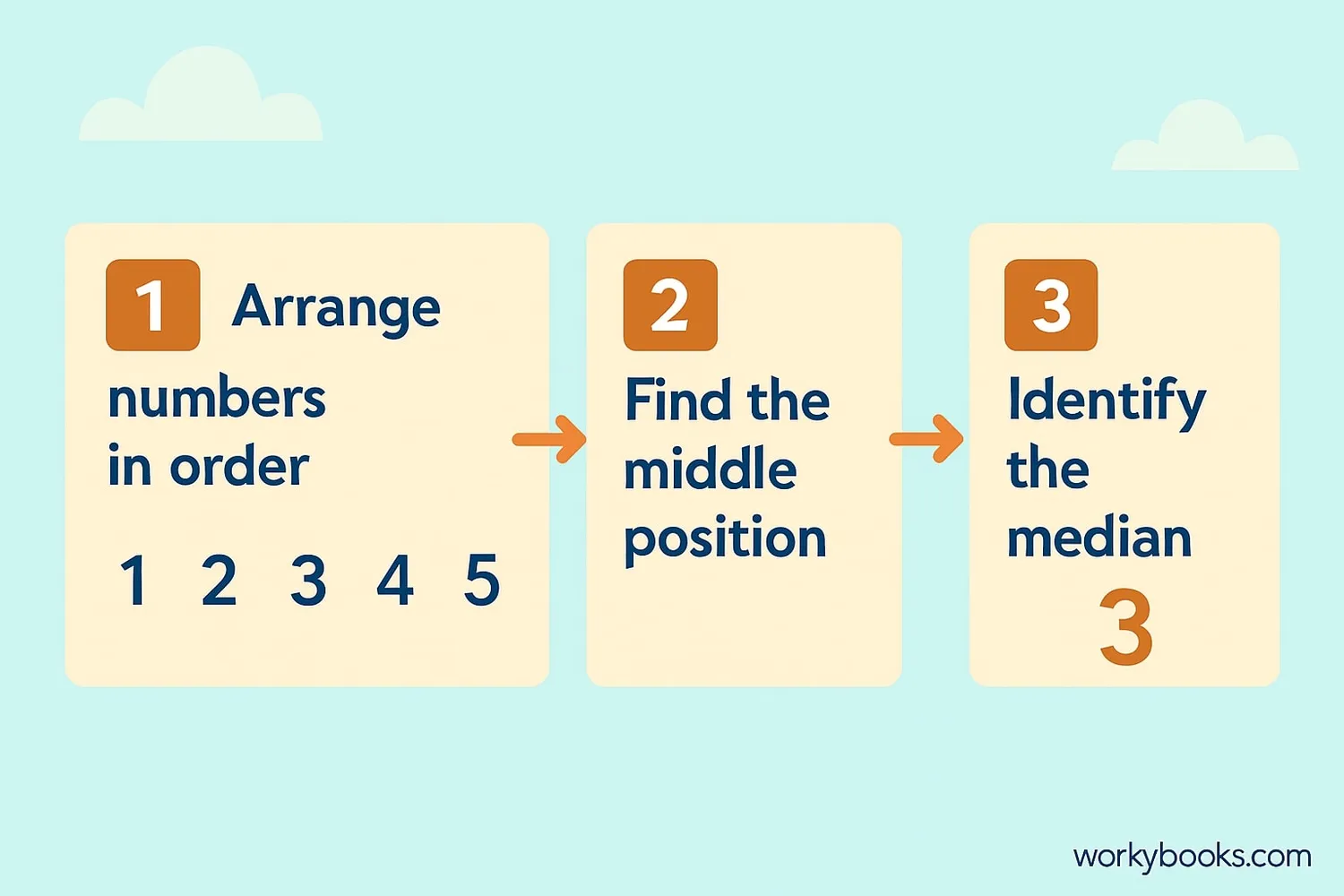
Finding the median is like finding the middle person in a line. Follow these simple steps:
Arrange the numbers in order
Put all the numbers in order from smallest to largest.
Find the middle position
Count how many numbers are in your list. The position of the median is:
Where "n" is the number of values in your data set.
Identify the median
If you have an odd number of values, the median is the middle number.
If you have an even number of values, the median is the average of the two middle numbers.
Remember
Always arrange the numbers in order before finding the median. This is the most important step!
Median Examples
Let's practice finding the median with some real-world examples:
Example 1: Test scores in math class: 85, 92, 78, 90, 88
Step 1: Order the numbers: 78, 85, 88, 90, 92
Step 2: Find the middle: 5 scores → position = (5+1)/2 = 3rd score
Step 3: Median = 88
Example 2: Ages of children at a party: 9, 7, 8, 10, 7, 6
Step 1: Order the numbers: 6, 7, 7, 8, 9, 10
Step 2: Find the middle: 6 values → positions 3 and 4
Step 3: Median = (7 + 8) ÷ 2 = 7.5
Example 3: Prices of toys: $15, $8, $22, $12, $18, $25, $10
Step 1: Order the numbers: 8, 10, 12, 15, 18, 22, 25
Step 2: Find the middle: 7 values → position = (7+1)/2 = 4th value
Step 3: Median = $15
Example 4: Number of books read: 4, 6, 3, 7, 5, 2
Step 1: Order the numbers: 2, 3, 4, 5, 6, 7
Step 2: Find the middle: 6 values → positions 3 and 4
Step 3: Median = (4 + 5) ÷ 2 = 4.5
Real-World Use
Median is often used for home prices, salaries, and test scores because it's not affected by extremely high or low values.
Median Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the median:
Data Trivia
Discover interesting facts about statistics and the median:
Historical Use
The concept of median dates back to the 16th century. Astronomers used it to make their measurements more accurate by ignoring extreme values caused by measurement errors.
Home Prices
Real estate websites always report the median home price rather than the average. This gives a better idea of typical home prices in an area without being skewed by a few very expensive properties.
Scientific Use
Scientists often use median instead of mean for data like reaction times or cell counts because biological data often has outliers that would distort the average.
Global Statistics
When countries report the "average" income of their citizens, they usually mean the median income. This gives a more accurate picture of what a typical person earns.


