Midpoint Formula - Definition, Examples, Quiz, FAQ, Trivia
Learn how to find the middle point between two locations with easy explanations and practice activities
What is the Midpoint?
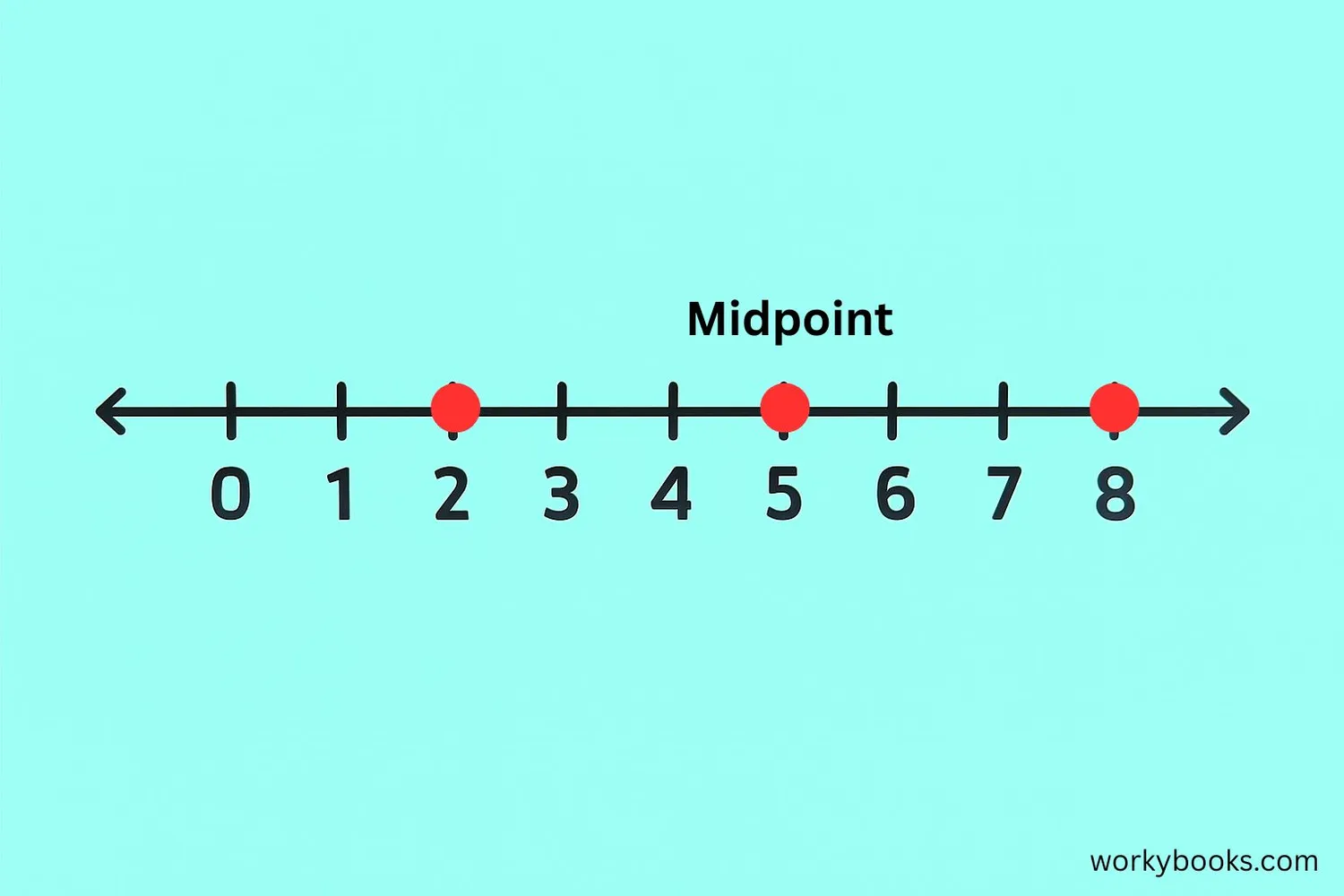
The midpoint is the exact middle point between two locations. Imagine you're standing between two friends - the spot exactly in the middle is the midpoint!
In math, we often find midpoints on number lines or coordinate grids. The midpoint has equal distance to both points.
For example:
- On a number line: The midpoint between 4 and 10 is 7
- On a map: The midpoint between your house and school is halfway
- In geometry: The midpoint of a line segment divides it into two equal parts
Key Concept
The midpoint is always exactly halfway between two points, with equal distance to both ends.
The Midpoint Formula
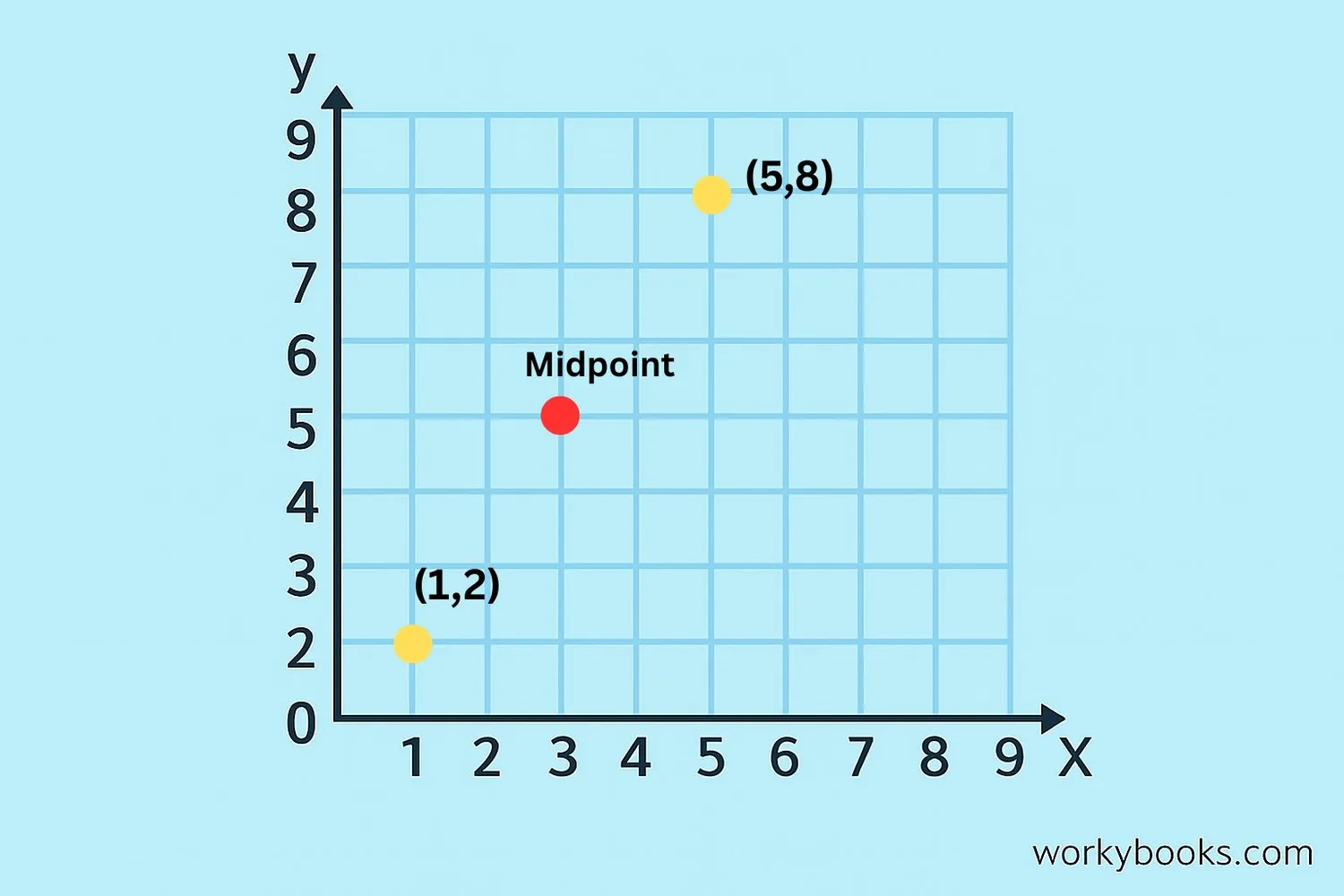
When we have two points on a coordinate grid, we use the midpoint formula to find the exact middle point:
Midpoint Formula
Where (x₁, y₁) and (x₂, y₂) are the coordinates of the two points
This formula tells us:
- Add the x-coordinates of both points and divide by 2
- Add the y-coordinates of both points and divide by 2
- The result is the (x, y) coordinates of the midpoint
Remember
The midpoint formula is like finding the average of the x-coordinates and the average of the y-coordinates!
How to Use the Midpoint Formula
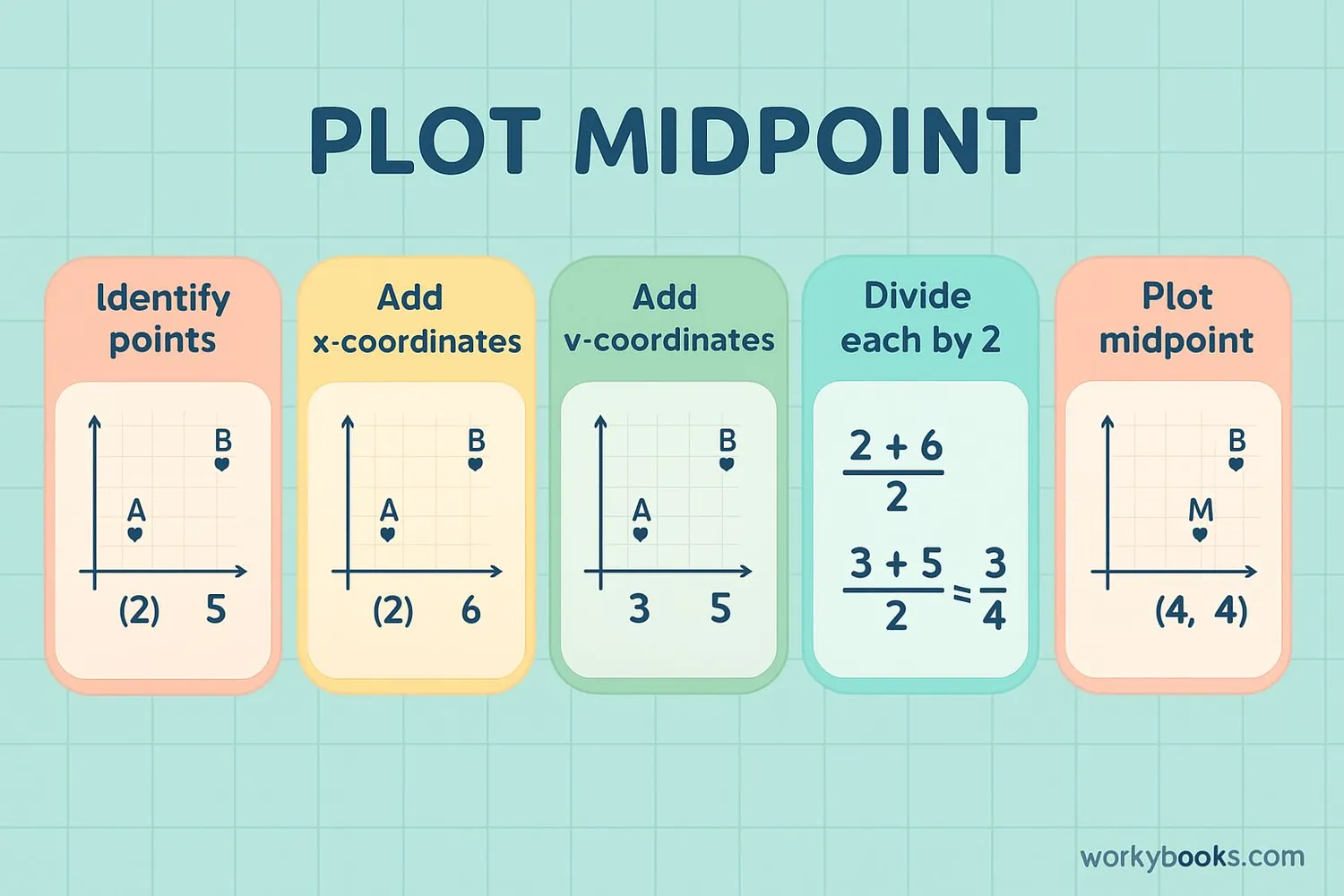
Let's find the midpoint between two points step by step:
Example: Find the midpoint between A(2, 4) and B(6, 10)
Step 1: Identify the coordinates
Point A: (x₁, y₁) = (2, 4)
Point B: (x₂, y₂) = (6, 10)
Step 2: Calculate the x-coordinate of midpoint
(x₁ + x₂)/2 = (2 + 6)/2 = 8/2 = 4
Step 3: Calculate the y-coordinate of midpoint
(y₁ + y₂)/2 = (4 + 10)/2 = 14/2 = 7
Step 4: Write the midpoint
Midpoint M = (4, 7)
That's it! The midpoint is at (4, 7). You can check by seeing that it's halfway between both points.
Tip
Always double-check your addition and division. A small mistake can give the wrong midpoint!
Practice Examples
Let's practice with more examples. Try to solve these before looking at the answers!
Example 1: Horizontal Line
Find the midpoint between (3, 5) and (9, 5)
Solution: Since y-coordinates are the same, we only need to average x-coordinates.
(3 + 9)/2 = 12/2 = 6
Midpoint = (6, 5)
Example 2: Vertical Line
Find the midpoint between (4, 2) and (4, 10)
Solution: Since x-coordinates are the same, we only need to average y-coordinates.
(2 + 10)/2 = 12/2 = 6
Midpoint = (4, 6)
Example 3: Diagonal Line
Find the midpoint between (1, 3) and (7, 9)
Solution: Average both coordinates
x = (1 + 7)/2 = 8/2 = 4
y = (3 + 9)/2 = 12/2 = 6
Midpoint = (4, 6)
| Point A | Point B | Midpoint |
|---|---|---|
| (0, 0) | (8, 0) | (4, 0) |
| (2, 4) | (2, 10) | (2, 7) |
| (1, 5) | (5, 1) | (3, 3) |
| (3, 8) | (7, 2) | (5, 5) |
Pattern
Notice how the midpoint is always the average of the two points? This works for any two points!
Midpoint Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the midpoint formula:
Math Trivia
Discover interesting facts about geometry and midpoints:
Ancient Origins
The concept of midpoint dates back to ancient Egypt. Egyptians used midpoints in land surveying along the Nile River to fairly distribute farmland after annual floods.
Space Applications
NASA scientists use the midpoint formula when calculating trajectories for space missions. The midpoint between Earth and Mars helps determine the most efficient path for spacecraft.
Nature's Midpoints
Many patterns in nature involve midpoints. The veins on leaves often branch from midpoint positions, and some flowers arrange petals around midpoint centers.
Technology Uses
Your smartphone uses midpoint calculations constantly! GPS navigation, touchscreen responsiveness, and image processing all rely on finding midpoints between coordinates.





