Mixed Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn about mixed numbers, how to convert them, and solve problems with fractions
What are Mixed Numbers?

For example: 2
Mixed numbers are useful in everyday life. When you say "I have two and a half sandwiches," you're using a mixed number! They help us describe quantities that aren't whole numbers but include whole parts.
Key Concept
Every mixed number has two parts: a whole number and a proper fraction (where the numerator is smaller than the denominator).
Converting Between Mixed Numbers and Improper Fractions

We can convert between mixed numbers and improper fractions. An improper fraction has a numerator larger than its denominator.
Conversion Formula
To convert a mixed number to an improper fraction:
Example: Convert 2
Step 1: Multiply whole number by denominator → 2 × 2 = 4
Step 2: Add the numerator → 4 + 1 = 5
Step 3: Keep the denominator → 5/2
So 2
Converting Improper Fractions to Mixed Numbers
Adding and Subtracting Mixed Numbers

Adding and subtracting mixed numbers is similar to working with fractions, but we need to pay attention to the whole number and fractional parts.
Method 1: Convert to improper fractions
Step 1: Convert both mixed numbers to improper fractions
Step 2: Find a common denominator
Step 3: Add the numerators
Step 4: Simplify and convert back to mixed number if needed
Method 2: Add whole and fraction parts separately
Step 1: Add the whole number parts
Step 2: Add the fraction parts
Step 3: If the fraction is improper, convert it to a mixed number and add its whole part to the whole number total
Step 4: Simplify the fraction
Example: Adding Mixed Numbers
Remember
When subtracting mixed numbers, you might need to borrow from the whole number if the fraction you're subtracting is larger than the fraction you have.
Multiplying and Dividing Mixed Numbers
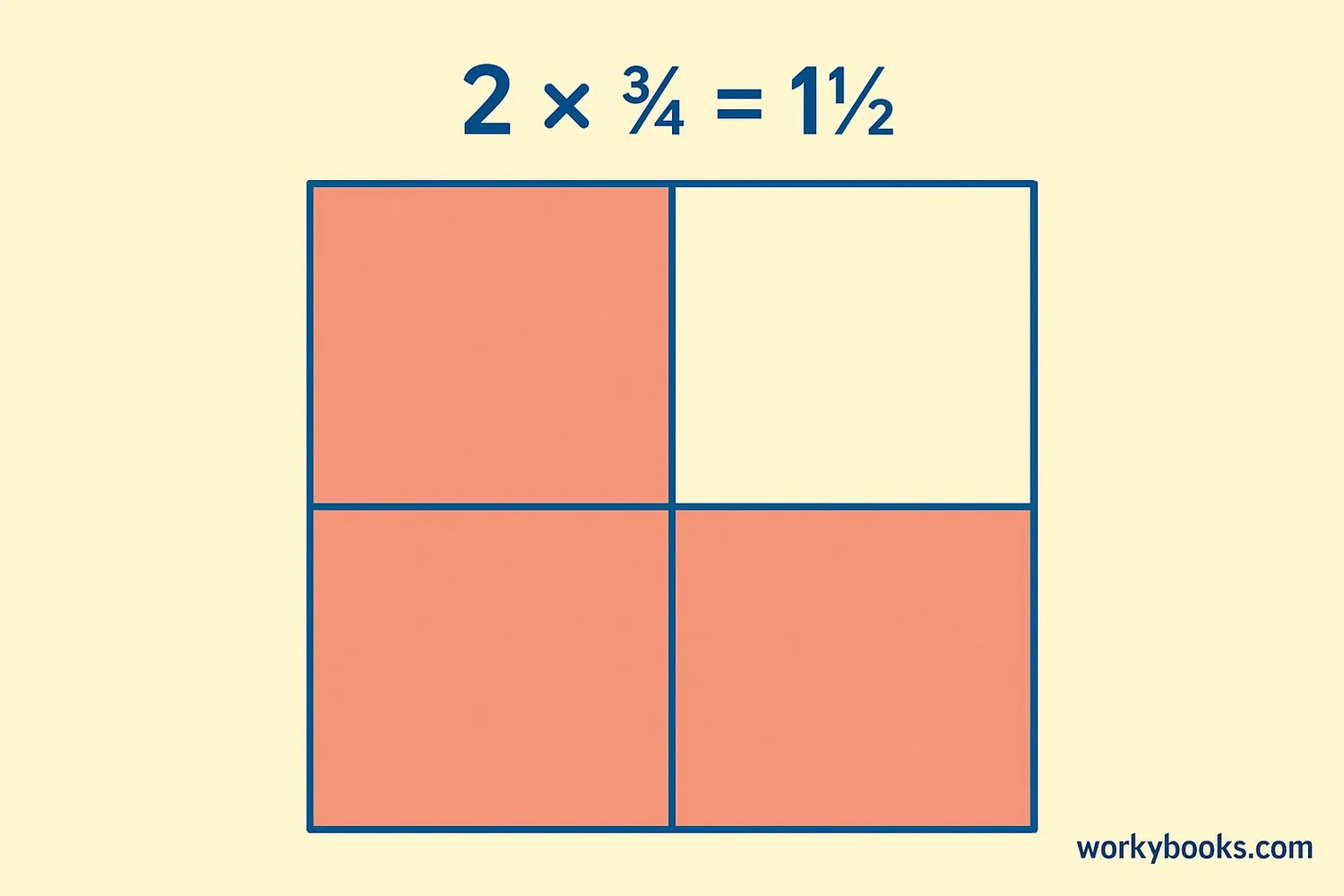
Multiplying and dividing mixed numbers requires converting them to improper fractions first. This makes the calculations easier.
Multiplying Mixed Numbers:
Step 1: Convert each mixed number to an improper fraction
Step 2: Multiply the numerators
Step 3: Multiply the denominators
Step 4: Simplify the resulting fraction
Step 5: Convert back to a mixed number if needed
Dividing Mixed Numbers:
Step 1: Convert each mixed number to an improper fraction
Step 2: Multiply the first fraction by the reciprocal of the second fraction
Step 3: Multiply numerators and denominators
Step 4: Simplify the resulting fraction
Step 5: Convert back to a mixed number if needed
Example: Multiplying Mixed Numbers
Mixed Numbers Practice Quiz
Test your understanding of mixed numbers with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about mixed numbers:
Fraction Trivia
Discover interesting facts about fractions and mixed numbers:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They had special symbols for fractions like ½, ⅓, and ¼, and represented other fractions as sums of these unit fractions.
Fractions in Nature
Fractions appear throughout nature! The Fibonacci sequence (1, 1, 2, 3, 5, 8, 13...) creates fractions that appear in flower petals, pinecones, and spiral galaxies.
Fractions in Music
Musical rhythms are based on fractions. A whole note lasts 4 beats, a half note 2 beats, a quarter note 1 beat, and so on. Time signatures like ¾ tell musicians how many beats are in each measure.
The Golden Ratio
The Golden Ratio (approximately 1.618) is a special fraction that appears in art, architecture, and nature. It's considered the most aesthetically pleasing proportion to the human eye.





