Multiplicative Inverse - Definition, Examples, Quiz, FAQ, Trivia
Discover the math magic of numbers that undo multiplication!
What is Multiplicative Inverse?
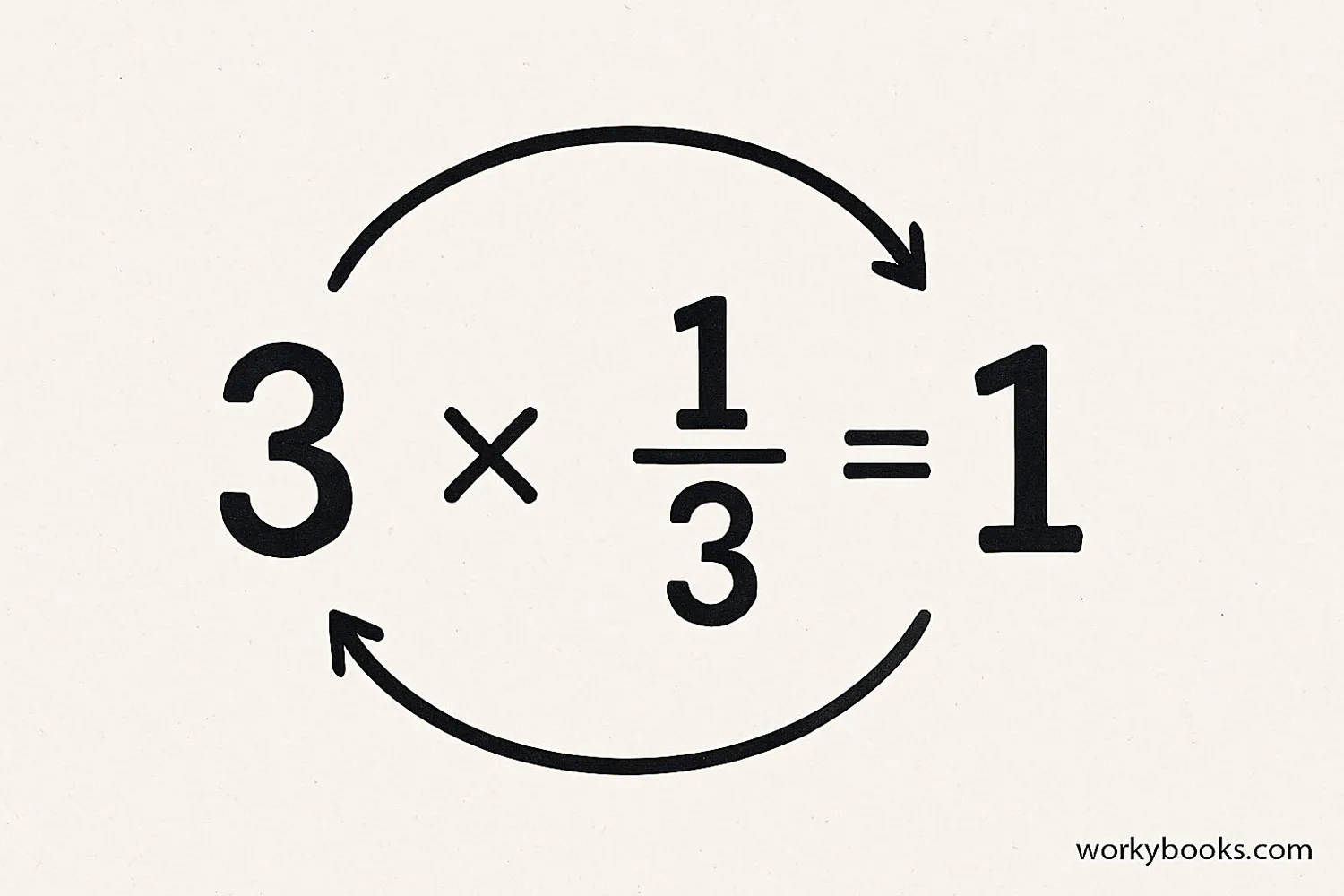
The multiplicative inverse of a number is a special number that, when multiplied by the original number, gives the answer 1. It's like having a math undo button! When you multiply a number by its multiplicative inverse, they cancel each other out.
For example, the multiplicative inverse of 5 is 1/5 because 5 × 1/5 = 1. Every number except zero has a multiplicative inverse.
Math Fact!
The multiplicative inverse is also called the reciprocal. These two terms mean the same thing in mathematics!
Reciprocal Numbers

Finding the reciprocal (multiplicative inverse) of a number is simple:
Whole Numbers
Write the number as a fraction (e.g., 5 = 5/1), then flip it (1/5)
Fractions
Flip the numerator and denominator (e.g., 2/3 becomes 3/2)
Mixed Numbers
First convert to improper fraction, then flip
Remember, the product of a number and its reciprocal is always 1. This is why they're called multiplicative inverses - they "undo" each other in multiplication.
Example:
Examples of Multiplicative Inverse
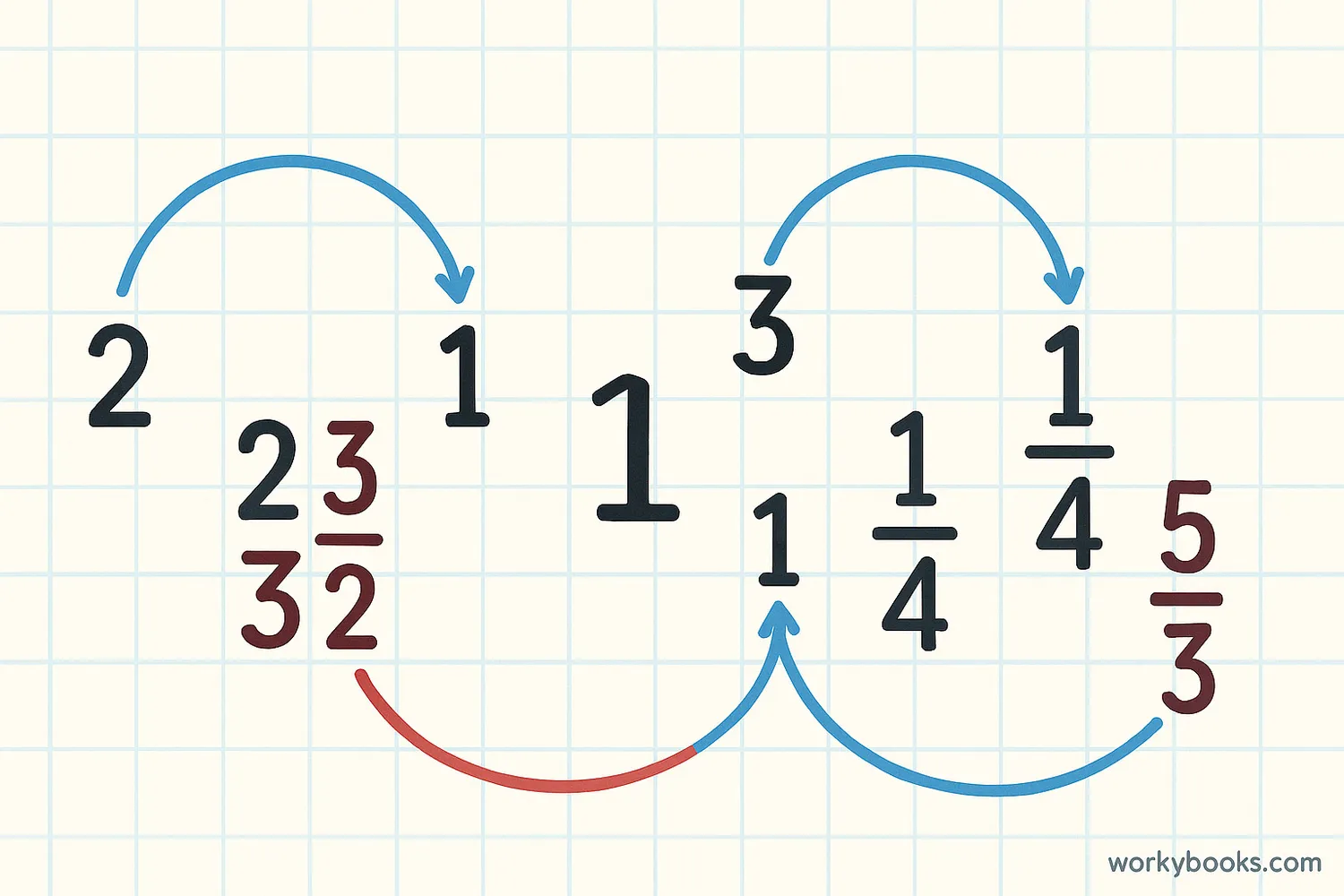
Let's look at some examples of multiplicative inverses:
Number: 2
Multiplicative Inverse: 1/2
Because 2 × 1/2 = 1
Number: 3/4
Multiplicative Inverse: 4/3
Because 3/4 × 4/3 = 12/12 = 1
Number: 10
Multiplicative Inverse: 0.1 or 1/10
Because 10 × 0.1 = 1
Number: 1
Multiplicative Inverse: 1
Because 1 × 1 = 1
Notice that the number 1 is its own multiplicative inverse. Also, zero (0) does not have a multiplicative inverse because you cannot multiply 0 by any number to get 1.
Fractions and Division
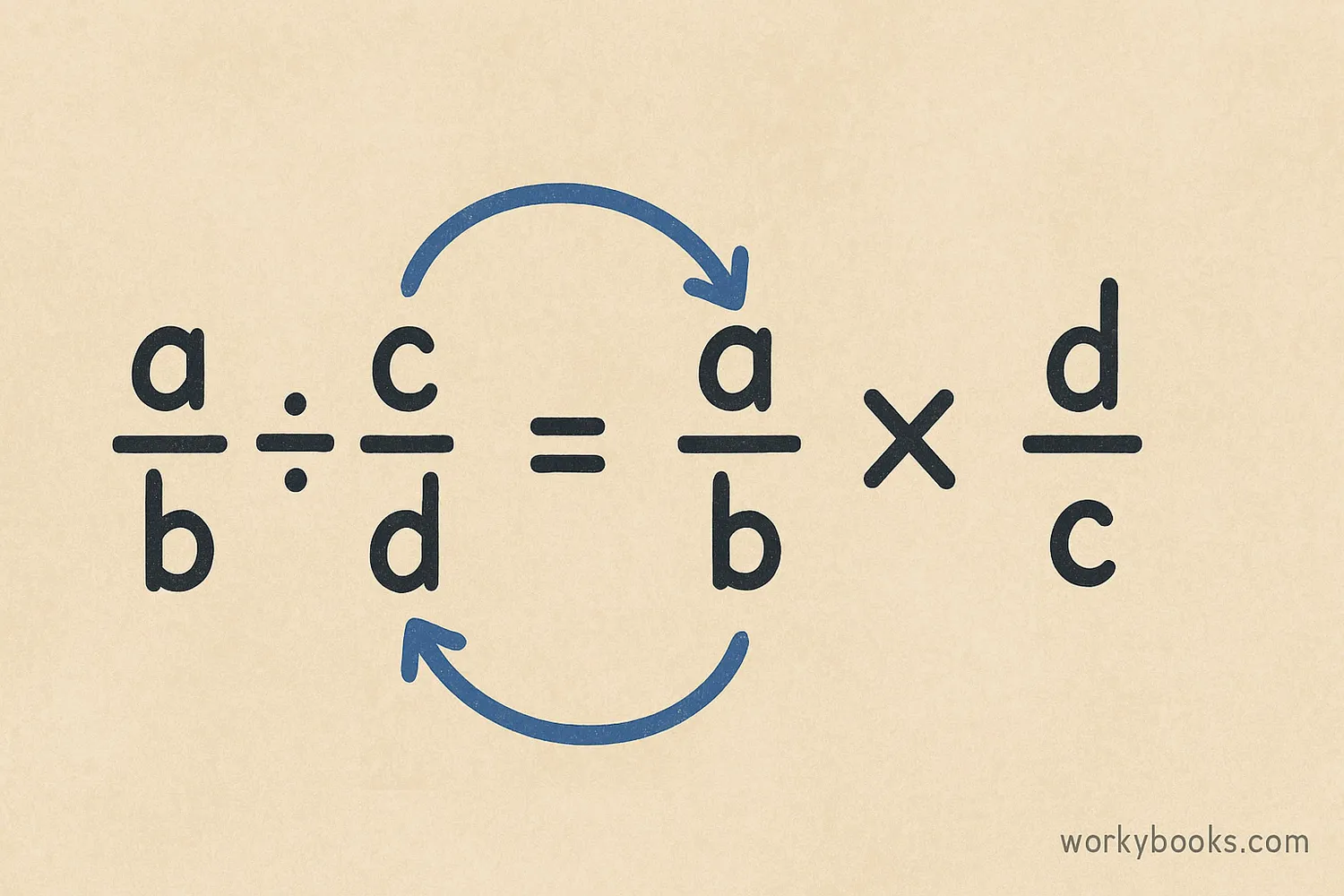
Multiplicative inverses are especially useful when working with fractions and division. Did you know that dividing by a fraction is the same as multiplying by its reciprocal?
This is why we "invert and multiply" when dividing fractions. We're actually multiplying by the multiplicative inverse of the divisor!
Division Example:
Instead of dividing by 2/3, we multiplied by its reciprocal 3/2
Math Tip!
When you need to divide by a fraction, just multiply by its reciprocal instead. This makes fraction division much easier!
Math Quiz
Test your knowledge about multiplicative inverses with this quiz! Answer all 5 questions to see how much you've learned.
Frequently Asked Questions
Here are answers to some common questions about multiplicative inverses:
Math Trivia
Discover some amazing facts about multiplicative inverses and mathematics!
Historical Origins
The concept of multiplicative inverses dates back to ancient Egyptian mathematics around 1800 BC. The Rhind Mathematical Papyrus shows that Egyptians used unit fractions (fractions with 1 as numerator) extensively in their calculations.
Calculator Magic
On many calculators, you can find the multiplicative inverse (reciprocal) of a number by entering the number and then pressing the 1/x button. This shows how important this concept is in mathematical computations.
Musical Relationships
In music, multiplicative inverses appear in the relationship between note frequencies. For example, if one note has frequency f, the note one octave higher has frequency 2f, and the note one octave lower has frequency (1/2)f.
Special Property of 1
The number 1 is the only positive integer that is its own multiplicative inverse. This special property makes 1 the multiplicative identity element - any number multiplied by 1 remains unchanged.





